к.ф.-м.н. Борисова М.Н., Артемьева Е.С.

Северо-Восточный Федеральный Университет им. М.К. Аммосова

Математическая модель индуцированных перенапряжений в линии передач при разряде молнии между облаками

Проблема электромагнитной совместимости технических сооружений с атмосферным электричеством в условиях многолетней мерзлоты имеет особую актуальность. Одним из аспектов этой проблемы являются вопросы повышения эффективности грозозащиты линий передач (ЛЭП, газо-нефте трубопроводы и т.п.) . При разряде молнии вблизи линии возникают кратковременные перенапряжения, или вызванные прямым попаданием молнии, или индуцированные. Методы защиты от прямых ударов молний достаточно хорошо разработаны. Однако, в регионах с высоким удельным электрическим сопротивлением грунта, к которым относятся и регионы с многолетней мерзлотой, часто наблюдаются множественные повреждения в линиях передач вдали от точки разряда молнии даже при отсутствии прямого попадания молнии в линию.

Общепринятый метод приближенного расчета индуцированных перенапряжений в воздушных линиях основан на вычислении электромагнитного поля, излучаемого каналом молнии. Это связано с решением системы уравнений Максвелла, при этом определяется горизонтальная составляющая электрического поля излучения канала молнии вблизи линии передачи, затем решается задача для системы телеграфных уравнений [1-5].

В данной работе предлагается другой подход к вычислению индуцированных перенапряжений, основанный на построении математической модели явления волны тока и напряжения (ВТН). Под действием электростатического поля грозового облака на проводниках линии передач индуцируются электрические заряды. При быстром разряде грозового облака эти заряды "высвобождаются" и, растекаясь по линии передач, образуют ВТН, в результате которой появляются грозовые перенапряжения [6,7]. Явление ВТН может инициировать аварийные явления в ЛЭП и трубопроводах, расположенных в регионах с многолетней мерзлотой. Есть сведения о том, что на линии передач, расположенные в полярных и субполярных широтах, интенсивные геомагнитные возмущения оказывают сильное влияние, вплоть до аварий [8].

Преимущество нашего метода по сравнению с другими состоит в математической простоте, легко можно моделировать случаи разрядов молнии в землю и между облаками, учесть наличие многолетней мерзлоты. В работах [6,7] аналитически и численно решены задачи о ВТН в предположении о мгновенном характере разряде молнии, рассмотрены случаи разряда молнии в землю и между двумя облаками. Здесь представлена математическая модель ВТН, учитывающая зависимость тока молнии от времени и аналитически решена задача о ВТН для случая произвольных погонных параметров R,C,L,G, проведены численные расчеты.

Математическая модель

Для простоты рассмотрим линию передач с одним проводником. Линия передач моделируется бесконечным тонким проводником, расположенным на высоте l над проводящим полупространством, параметр l характеризирует толщину многолетнемерзлого слоя. Линия характеризуется распределенными параметрами R, C, L, G - сопротивлением, емкостью, индуктивностью и коэффициентом утечки, рассчитанными на единицу длины. На высоте l над полупространством введем декартову систему координат, пусть ось х и линия передачи совпадают, ось z направлена перпендикулярно полуплоскости. Грозовые облака моделируется двумя точечными зарядами Q и -Q, расположенными в точках с координатами (x₁, y₁, z₁) и (x₂, y₂, z₂).

Следовательно, линия находится в поле зарядов -Q, Q, и их электростатических изображений (Рис. 1).

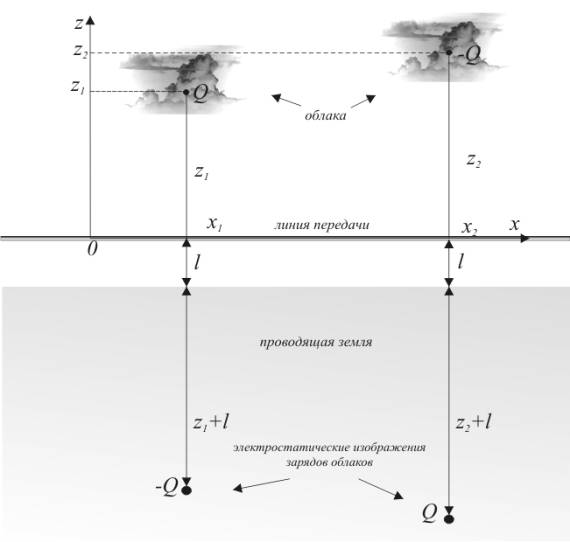
Рис. 1 Разряд молнии между облаками

Разряд молнии между этими двумя облаками соответствует мгновенному исчезновению всех этих точечных зарядов. Тогда, для определения силы тока i(x, t) и напряжения u(x, t) в линии передачи после такого разряда грозовых облаков, получаем задачу Коши для системы телеграфных уравнений:

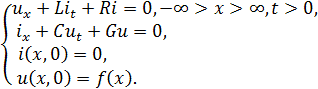(1)

Начальная функция f(x) равняется потенциалу четырех точечных зарядов, два из которых являются электростатическими изображениями зарядов, моделирующих грозовые облака:

где

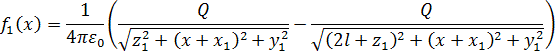
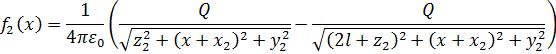
Аналитическое решение

Используя стандартные методы математической физики [9] аналитическое решение задачи (1), описывающей ВТН получаем в следующем виде:

,

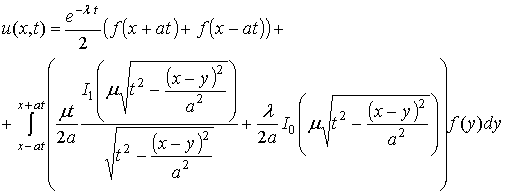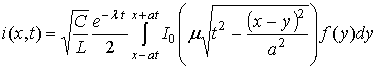
где и – модифицированные функции Бесселя.

В случае выполнения условия отсутствия искажения:

Решение задачи упрощается, и принимает вид:

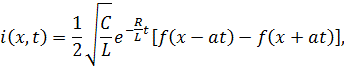
Численное решение

Геометрические параметры трубопровода получены из отчета [10]

– внешний радиус трубопровода,

- внутренний радиус трубопровода.

Физические постоянные величины:

- электрическое постоянное,

- магнитное постоянное,

- удельное сопротивление проводника.

Расположение проводника между облаками и землей [11]

- толщина многолетней мерзлоты,

- расстояние от проводника до облака.

Численные значения погонных параметров трубопровода (индуктивности, сопротивления и емкости) для двухпроводной линии с полными проводами [12,13]

- погонная емкость трубопровода,

– погонное сопротивление трубопровода,

- погонная индуктивность трубопровода,

– скорость ВТН в проводнике.

Ниже приведем примеры расчетов для безразмерных величин силы тока и напряжения.

1. На Рис. 2 и Рис. 3 для разных моментов времени приведены результаты расчетов при ударе молнии между облаками, когда проекция молнии перпендикулярна линии передач.

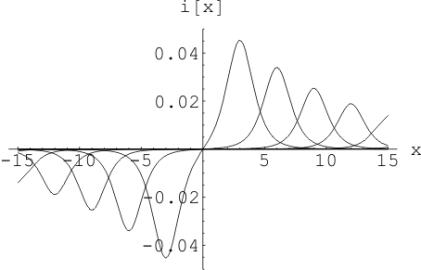
Рис. 2. Волна силы тока, координаты облаков: , коэффициент утечки трубопровода в разные моменты времени

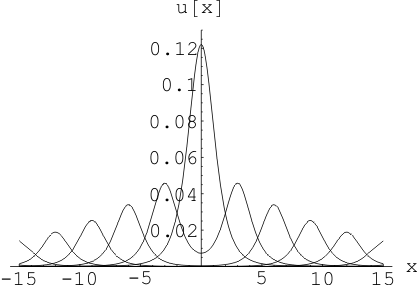
Рис. 3 Рис. 2. Волна напряжения, координаты облаков: , коэффициент утечки трубопровода в разные моменты времени

Геометрическое расположение облака: , коэффициент утечки трубопровода . Как видно из графиков, ВТН возникает как при ударе молнии о землю (максимальные значения величин . Расчеты показали, что при в линии передач не образуется ВТН. Это соответствует физическому смыслу, т.к. в данном случае имеем полностью геометрически симметричную ситуацию и магнитное поле тока молнии будет направлено вдоль линии передачи, а электрическое поле - перпендикулярно, что приводит к отсутствию наведенных токов.

2. На Рис. 4 и Рис. 5 приведены результаты, когда проекция молнии не перпендикулярна линии передачи.

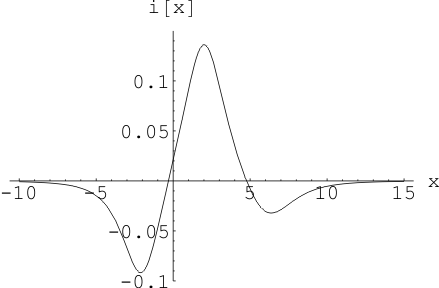
Рис. 4 Волна силы тока, координаты облаков: , , , , коэффициент утечки трубопровода в момент времени

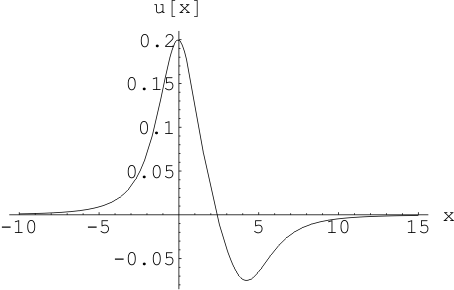
Рис. 5. Волна напряжения, координаты облаков: , , , , коэффициент утечки трубопровода в начальный момент времени.

Геометрическое расположение облаков: , , , ; коэффициент утечки . Для силы тока максимальная амплитуда образовалось в момент времени а для напряжения в момент времени Расчеты показывают, что для силы тока (Рис.4) образуется четыре волны и когда две встречные волны суммируются образуется максимальная амплитуда. Эта амплитуда оказывается больше соответствующей максимальной амплитуды, когда молния образуется только от первого облака (удар молнии в землю). На Рис.5 показана волна напряжения в начальный момент, когда она имеет максимальное амплитудное значение (

3. На Рис.6 и Рис.7 приведены результаты, когда проекция молнии параллельно линии передач.

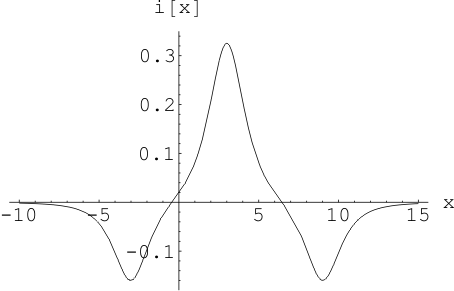
Рис. 6 Волна силы тока, координаты облаков: , , , , коэффициент утечки трубопровода в момент времени

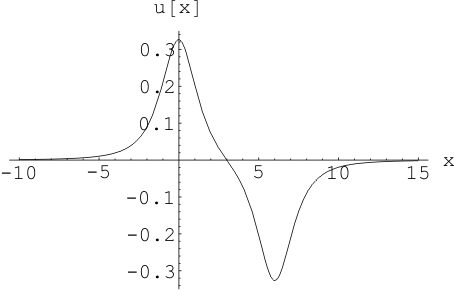
Рис. 7 Волна напряжения, координаты облаков: , , , , коэффициент утечки трубопровода в начальный момент времени.

Геометрическое расположение облаков: , , , , коэффициент утечки трубопровода для силы тока максимальная амплитуда образовалось в момент времени , а для напряжения в момент времени . Видно, что максимальное значение для силы тока Рис. 6 получается четыре волны одинаковые по модулю. Две волны суммируются и образуют максимальное амплитудное значение силы тока (

4. На Рис. 8 и Рис.9 приведены результаты, когда облака находятся в разных высотах.

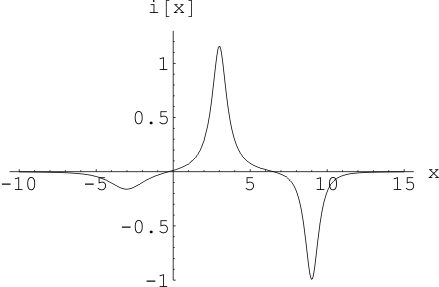
Рис. 8 Волна силы тока, координаты облаков: , , , , коэффициент утечки трубопровода в момент времени

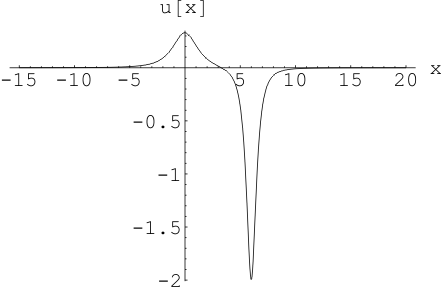
Рис. 9 Волна напряжения, координаты облаков: , , , , коэффициент утечки трубопровода в начальный момент времени.

Геометрическое расположение облаков: : , , , ; коэффициент утечки Для силы тока максимальная амплитуда образовалось в момент времени, а для напряжения в момент времени . Результаты показывают, что форма ВТН зависит от высоты облаков над линией передач. Чем ниже облако тем больше амплитуда ВТН. ()

На Рис.10 приведены результаты зависимости тока молнии от проекции расстояния между облаками и от высоты облаков.

Рис. 10 Зависимость тока молнии от геометрического расположения облаков.

Из графика видно, что существует некий пик зависящий от расстояния между облаками, которое приводит к максимальному значению ().

Далее на Рис. 11 приведен пример сравнения максимальных значений силы тока при различных значениях коэффициента утечки.

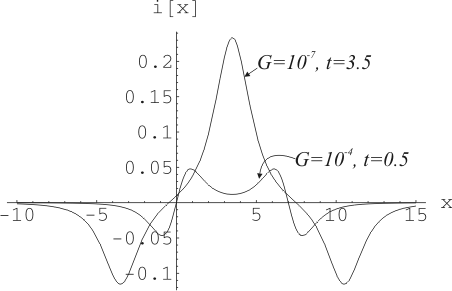
Рис. 11. Сравнение максимальных значениях амплитуды силы тока при и .

Координаты облаков: , , , ; коэффициент утечки в момент времени () и коэффициент утечки в момент времени ().

На Рис. 12 приведено сравнение максимальных значений силы тока в зависимости от коэффициента утечки линии передач и от расстояния между облаками, где координаты облаков в данном случае: , ,

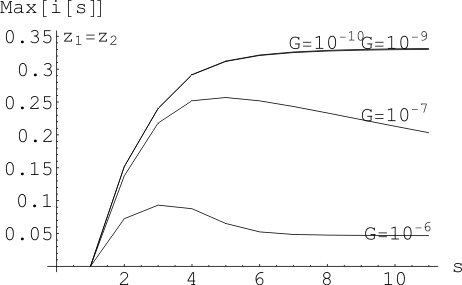
Рис. 12 Сравнение максимальных значений силы тока при различных значениех G, когда облака расположены параллельно линии передач

Выводы

Анализ полученных численных результатов показал, что распределения токов и напряжений вдоль проводника, индуцированных при межоблачном разряде молнии, являются более сложными, чем при ударе молнии о землю. Имеется распространяющийся вдоль проводника фронт волны с нулевыми значением тока. В рассматриваемой задаче критическими параметрами являются максимальные значения напряжений и токов. Расчетами установлены закономерности изменения этих параметров в зависимости от геометрического расположения облаков и коэффициента утечки. Например, максимальное значение силы тока зависит от расстояния между облаками и проводником. Чем ближе расположены облака, тем меньше амплитуда возникающей ВТН.

При этом в отличие от других авторов для расчета индуцированных перенапряжений принимается во внимание явление ВТН и не решается система уравнений Максвелла, что существенно упрощает математическую модель. Проведенные численные оценки показывают, что величины ВТН достигают величин, достаточных для возникновения аварийных ситуаций в линии передачи.

Литература

1. Костенко, М.В. Перенапряжение и защита от них в воздушных и кабельных электропередачах высокого напряжения / Костенко М.В. - Ленинград, 1988 - С. 301

2. Rachidi, F. Calculation methods of the horizontal component of lightning return stroke electric fields / F. Rachidi, M. Ianoz, C.A. Nucci, C. Mazzetti. / Eleventh International Wroclaw Symposium and Exhibition on Electromagnetic compatibility September 2-4, 1992. - Wroclaw, 1992. - P. 452 - 456.

3. Левкин, Н.Е, Анализ грозовых перенапряжений в ВЛ и на подстанциях 35 кВ. / Левкин, Н.Е, Гумерова Н.И. / М/н конференция "Перенапряжения и надежность эксплуатации электрооборудования". Вып. 2. Материалы м/н научно-технической конференции 31.03-05.04.2008 г., г. С-Петербург, 2003. - С-Петербург: Изд. ПЭИПК, 2003. - С. 104-111.

4. Yoshihiro, B. Voltages induced on an overhead wire by lightning strikes to a nearby tall grounded object / Yoshihiro Bara, Vladimir A. / IEEE transaction on electromagnetic compatibility, vol. 48, no. 1, February 2006 - P. 212-224.

5. Ефимов, Б.В. Теория распространения волн атмосферных перенапряжений в многопроводных коронирующих линиях / Ефимов, Б.В. / Электрофизические проблемы надежности эксплуатации высоковльтных сетей и цепей управления. - Апатиты 1999 г. С.20-41.

6. Григорьев, Ю.М. Расчет волны тока индуцированной разрядом молнии в кабельных линиях / Ю.М. Григорьев, С.Н. Еремеев, В.В. Наумов, А.А. Семенов. / Десятый международный Вроцлавский симпозиум по электромагнитной совместимости, 26-29 июня, 1990 г. - Вроцлав, 1990, С. 247-252.

7. Григорьев, Ю.М.. Математические модели грозовых перенапряжений в линиях передач / Григорьев, Ю.М., Орлова М.Н. / VII Лаврентьевские чтения. Научная конференция. Секция "Математика, механика и физика". Сб. статей. Том I. 7-11 апреля 2003 г. - Якутск, 2003 г. - С. 29-33.

8. Matti, Lahtinen. GIC occurrences and GIC test for 400 kV system transformer / Matti Lahtinen. / IEEE transaction on power delivery, vol. 17, NO. 2 , april 2002. P. 555-561.

9. Тихонов, А.Н. Уравнения математической физики / А.Н.Тихонов, А.А.~Самарский. - Москва: Наука, 1977. - 736 с.

10. "Анализ изменений в Экзогенных геологических процессах и явлениях происшедших в окружающей среде вдоль трасс I и II ниток Магистрального газопровода СВГКМ-Мастах-Берге-Якутск, при эксплуатации на протяжении с 1967 по 1999 гг." ОАО "Якутгазпром" Технический отдел. - Якутск 1999г.

11. Михайлов М.И. Влияние внешних электромагнитных полей на цепи проводной связи и защитные мероприятия. -- Москва:Связьиздат, 1959. -- 583 с.

12. Тамм И.Е. Основы теории электричества. -- Москва: Наука, 1976- 616 с.

13. П.Л.Калантаров, Л.А.Цейтлин. Расчет индуктивности - Ленинград, 1986.