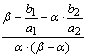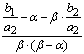Д.т.н., профессор Плаксиенко В.С., к.т.н., доцент Плаксиенко Н.Е.

Южный федеральный университет, Таганрог, Россия

Определение полосы захвата системы ФАПЧ при
прямоугольной характеристике ФД

При расчете полосы захвата систем фазовой автоподстройки частоты (ФАПЧ) любого порядка с прямоугольной характеристикой фазового детектора (ФД) применяют метод переходных характеристик [1,2]. Определять полосу захвата при прямоугольной характеристике ФД, реализуемой дискриминаторами с обратными связями [3] целесообразно по двум причинам: ‒ полоса захвата при прямоугольной характеристике ФД максимальна и полученное при расчетах значение можно рассматривать как предельное для выбранного фильтра нижних частот (ФНЧ) и различных характеристиках ФД; ‒ знание точного значения полосы захвата позволяет оценить точность приближенных методов расчета, пригодных при произвольных характеристиках ФД.

В ряде случаев в кольце ФАПЧ необходимо иметь ФНЧ, у которого частотная характеристика имеет крутые спады. Такая задача решается синтезом сложных фильтров. Задача определения основных характеристик кольца ФАПЧ при сложных ФНЧ решена приближенно. При расчете полосы захвата по приближенным формулам возникает большое расхождение между экспериментальными и расчетными данными. Определим полосу захвата системы ФАПЧ при прямоугольной характеристике ФД и произвольном ФНЧ на основании критерия исчезновения циклического режима в системе ФАПЧ.

В системе ФАПЧ с прямоугольной характеристикой ФД и произвольным ФНЧ в установившемся режиме биений разность фаз непрерывно увеличивается (рис. 1,а), и напряжение на выходе ФД имеет вид последовательности прямоугольных импульсов (рис. 1,б). В этой последовательности интервалы времени T₁ и T₂ постоянны, где T₁ – интервал времени, соответствующий изменению фазы от 2·π·k до 2·π·k+π , т.е. положительному напряжению на выходе ФД, T₂ – интервал времени, соответствующий изменению фазы от 2·π·k+π до 2·π·k+2·π, т.е. отрицательному напряжению на выходе ФД.

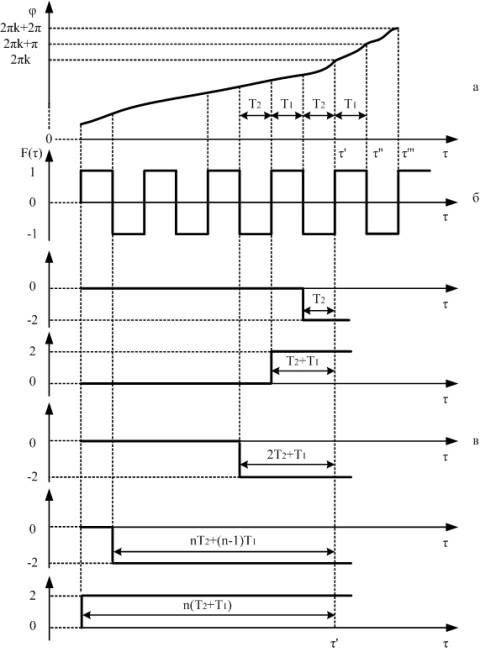
Рис. 1. К пояснению критерия исчезновения циклических колебаний

Сумма интервалов T₁ и T₂ определяет длительность цикла колебаний.
Время действия τ_i определяется через сумму интервалов T₁ и T₂. Знак определяется знаком соответствующей ступеньки. За время T₁ и за время T₂ фаза изменяется на π, а за время T₁+T₂ – на 2·π. Последовательность импульсов представляем в виде суммы функции включения, тогда значение разности фаз в любой момент времени определяем через сумму откликов на функцию включения. Запишем условия в виде двух уравнений:

(1)

_,(2)

где .

Если уравнения (1) и (2) имеют действительное решение, то в схеме может существовать режим циклических колебаний, т.е. существует предельный цикл второго рода. Значение расстройки, при которой исчезает действительное решение системы уравнений (1) и (2), определяет границу, при которой исчезают циклические колебания. В этом случае наступает режим захвата.

На основании полученного критерия можно рассчитать полосу захвата системы ФАПЧ с прямоугольной характеристикой ФД при любом ФНЧ, если известен его коэффициент передачи [1].

Пусть в кольце ФАПЧ используются ФНЧ типа 1/1 или 1/2. Коэффициент передачи для ФНЧ типа 1/1 имеет вид: ; для ФНЧ типа 2/2 коэффициент передачи имеет вид: .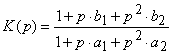

Переходную функцию q(τ) запишем в обобщенном виде:

. (3)

Значения коэффициентов α, β, A, B, и C уравнения (3) для разных типов фильтров приведены в таблице.

Значение коэффициента		K(p)	α	β	A	B	C
Тип ФНЧ	1/1			0	a1-b1	0	b1-a1
	2/2

Подставив значение переходной функции (3) в уравнения (1), (2) и заменив в них геометрические прогрессии предельными суммами, получим выражения:

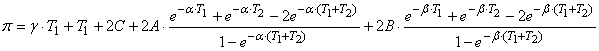(4)

. (5)

Из уравнения (5) находим интервал времени T₂:

. (6)

Так как этот интервал отличен от нуля, то на величину интервала T₁ накладывается условие:

. (7)

Подставляя значение T₂ из (6) в уравнение (4), получим одно уравнение, соответствующие условию существования режима циклических колебаний:

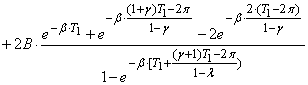. (8)

Запишем (8) в виде F=F₁-F₂-F₃, где F₁, F₂, F₃ определяются соотношениями:

; ;

.

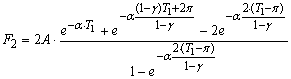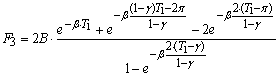Функция F(T₁) для различных значений начальной расстройки имеет вид, изображенный на рис. 2. Если начальная расстройка меньше полосы захвата, то функция F(T₁) лежит выше оси абсцисс, т.е. уравнение (8) не имеет действительного решения, в системе наступает захват.

Если начальная расстройка больше полосы захвата, то функция имеет две точки пересечения с осью абсцисс и в системе возможен режим биений. Полоса захвата определяется значением расстройки γ, при котором функция F(T₁) касается оси абсцисс (рис. 2).

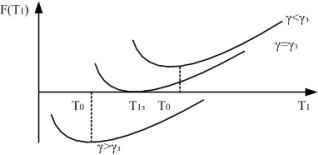
Рис 2. График функции F(T1)

Рассмотрение кривых на рис. 2 показывает, что если решение уравнения (9) существует, то оно лежит в той области значений параметра T₁, для которых функция F(T₁) положительна.

Из условия F(T₁)>0 определяем максимальное значение интервала T_1max:

. (9)

Знание границ интервала T_1min (7) и T_1maх (9), в котором лежит искомое решение уравнения (8), облегчает вычисление полосы захвата γ. При расчете γ, определяя точку касания T_1з, одновременно с полосой захвата можно рассчитать период циклических колебаний T в момент захвата. Согласно (8) он равен:

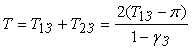. (10)

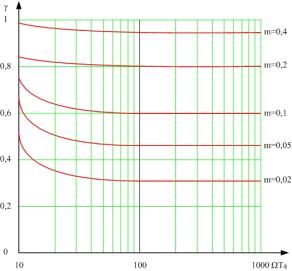
F₃=0, поэтому для пропорционально-интегрирующего ФНЧ типа 1/1 расчет упрощается. Результаты расчета полосы захвата на рис. 3. Полоса захвата уменьшается с ростом постоянной времени фильтра и возрастает при увеличении отношения .

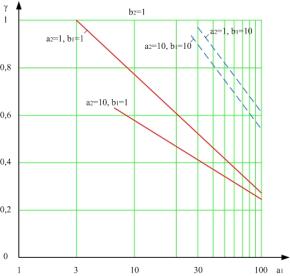
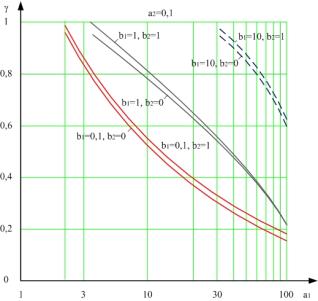
Для системы ФАПЧ с ФНЧ типа 2/2 на рис. 4 и 5 приведены графики зависимости полосы захвата от параметров фильтра a₁, a₂, b₁ и b₂.

Выводы: Из анализа полученных результатов можно сделать вывод: полоса захвата системы ФАПЧ с прямоугольной характеристикой ФД уменьшается с ростом a₁ и a₂ (рис. 4) и увеличивается с ростом b₁ и b₂ (рис. 5). При этом на значение полосы захвата наибольшее влияние оказывает коэффициент b_1.

Рис 3. Зависимость полосы захвата системы ФАПЧ γ при ФНЧ типа 1/1	Рис 4. Зависимость полосы захвата системы ФАПЧ γ при ФНЧ типа 2/2
Рис 5. Зависимость полосы захвата системы ФАПЧ γ при ФНЧ типа 2/2	ЛИТЕРАТУРА 1 Самойло К.А., Федосова Т.С. Критерий исчезновения режима циклических колебаний в системе ФАПЧ. – Изв. вузов СССР, Радиоэлектроника,1975, т. 18, №11. 2 Шахгильдян В.В., Ляховкин А.А. Системы фазовой автоподстройки частоты. М., «Связь», 1972. – 447 с.

3. Плаксиенко В.С., Плаксиенко Н.Е. Система ФАПЧ с дискриминатором с управляемой характеристикой. Материалы УШ международной НПК «VEDECKY POKROK NA PRELOMU TYSYACHALETY ‒ 2012» 27 kvetna – 05 cerna 2012 roku. Praha Publishing House «Education und Science» s.r.o 2012 pp. 29-32.