Економічні науки / 8. Математичні методи в економіці
Кухар О.В.,
к.е.н. доцент Потапова Н.А
Вінницький
національний аграрний університет, Україна
Економетричне моделювання при оцінці пливу витрат на собівартість продукції
Виконувати раціональне управління
всією економіко-виробничою системою при великому обсязі даних з урахуванням
швидких змін без економіко-математичного моделювання неможливо, оскільки це є
важливим напрямком удосконалення економічного аналізу, який підвищує
ефективність діяльності підприємств. У наш час моделювання є невід’ємною сферою
управління, тому що на діяльність
підприємства впливає ряд чинників, які потребують своєчасного та адекватного
реагування. Їх результат можна оцінити за допомогою кількісних методів
дослідження, основу яких становлять економіко-математичні моделі.
Економетричне моделювання дає змогу
вивчити та кількісно визначити внутрішні й зовнішньо-наслідкові зв’язки між
показниками економічних систем, установлювати закономірності їхнього формування
і тенденції розвитку. При цьому будується прогнозна модель, що характеризує
залежність досліджуваного параметра від ряду факторів, що на нього впливають [2].
Основними причинами швидкого поширення
методів економіко-математичного моделювання
є можливість формального опису зв'язків між економічними змінними,
допомога у розв'язанні задач
оптимізації планування та управління, високий рівень розвитку виробництва,
зростанням темпів науково-технічного прогресу, вимоги щодо підвищення
ефективності використання природних ресурсів [1, с.259].
Широкого розповсюдження набули
методи математичної статистики, які застосовуються в тих випадках, коли зміну
аналізованих показників можна представити як випадковий процес. Дані методи є
основним засобом вивчення масових, повторюваних явищ та відіграють важливу роль
у прогнозуванні поведінки економічних показників.
Матричні методи використовуються для
дослідження складних і великорозмірних економічних структур. Вони дають змогу
у найбільш стислій формі представити взаємозв'язок витрат і результатів виробництва, що важливо при великих обсягах
інформації.
Методи математичного програмування
призначені для оптимізації виробничо-господарської діяльності, оскільки вони дають
змогу оцінювати потенціал, обмежені види сировини і матеріалів, ступінь конкурентності
та ін.
Для прийняття управлінських рішень в
умовах ризику і невизначеності на підприємствах варто використовувати теорію
ігор. Теорія ігор - це сукупність математичних методів і моделей, пов'язаних
із прийняттям раціональних рішень в умовах конфлікту та невизначеності.
Методи дослідження операцій
використовуються в аналізі для отримання порівняльної оцінки альтернативних
рішень. Вони побудовані на використанні
досвіду та інтуїції спеціалістів при розв'язуванні аналітичних задач.
В основі економетричних методів
лежить економічна модель, під якою розуміють представлення економічного явища
чи процесу за допомогою наукової абстракції. Одним із основних розділів
економетрики є кореляційно-регресійний аналіз, в процесі якого
оцінюється тіснота статистичного зв'язку між досліджуваними змінними.
Основне завдання даного аналізу полягає в дослідженні залежності
досліджуваної змінної від різних факторів і відображенні їх взаємозв'язку у
формі регресійної моделі [3].
При побудові прогнозних моделей найчастіше
використовується парний і множинний регресійний аналіз.
У загальному
випадку парна лінійна регресія є лінійною функцією між залежною змінною Y і
однією пояснюючою змінною X:
, (1)
де Y - оцінювана чи прогнозована залежна змінна, X - пояснююча
змінна, 
і 
- параметри (теоретичні коефіцієнти)
регресії.
Коефіцієнти 
і 
розраховуються на основі спостережень величин Y і X за допомогою
методу найменших квадратів.
- вільний член
рівняння: 
(2)
- коефіцієнт регресії, що вимірює середнє відношення відхилення
результативної ознаки від його середньої величини до відхилення факторної
ознаки від його середньої величини на одну одиницю його виміру - варіація Y, що
приходиться на одиницю варіації X.
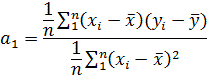
Аналіз на основі множинної регресії
заснований на використанні більш, ніж однієї незалежної перемінної у рівнянні
регресії. Це ускладнює аналіз, але регресійна модель повніше відбиває дійсність,
тому що в реальності досліджуваний параметр залежить від безлічі факторів. Усе,
що стосується множинної регресії є ідентичним парній регресії, тільки
використовується більш, ніж одна перемінна.
Багатофакторне рівняння множинної
регресії має наступний вид:
(4)
де Y - оцінювана чи прогнозована залежна змінна, X - пояснююча
змінна, 
і 
- параметри (теоретичні коефіцієнти)
регресії, m - число
незалежних перемінних (факторних ознак) [4].
У даній роботі досліджено
апробовані моделі впливу витрат на
прибуток ВАТ "Мурованокуриловецького заводу мінеральної води
"Регіна", що iснує більше 50 рокiв. Основною продукцiєю ВАТ
МКЗ"Регiна" є мiнеральна вода "Регiна" та безалкогольнi
напої. Розлив мiнеральної води "Регiна" здiйснюється у ПЕТ-пляшки
рiзної ємкостi: 1,5л., 0,75 л., 0,5 л., 5 л., 1 л.
На сьогоднiшнiй день в Українi є
дуже багато виробникiв мiнеральних вод, що суттєво впливає на попит продукцiї
пiдприємства. Оскільки конкуренція на ринку мінеральних вод висока, було проаналізовано вплив витрат на формування
собівартості продукції, а також визначена залежність ціни продукції від
собівартості для 1,5л. газованої мінеральної води "Регiна".
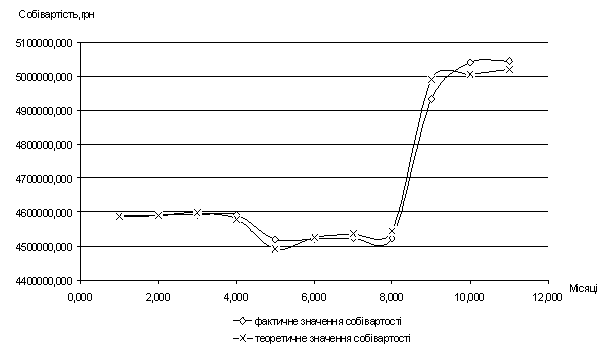
Вплив на собівартість матеріальних
витрат, зарплати, досліджень можна представити у вигляді рівняння (5) та у
вигляді графіку (1).
, (5)
де 
собівартість газованої мінеральної води
"Регiна", 
зарплата, 
дослідження, 
матеріальні витрати на виготовлення продукції.
|
6 місяців 2008 |
рік 2008 |
6 місяців 2009 |
рік 2009 |
6 місяців 2010 |
рік 2010 |
Рис.1 Вплив витрат на собівартість
1,5л. газованої
мінеральної води "Регiна"
Адекватність побудованого рівняння
регресії оцінюється коефіцієнтом
множинної кореляції R = 0,9928 (характеризує тісну
лінійну залежність між собівартістю та витратами), коефіцієнтом
детермінації R2=98,57% (зміна значення собівартості
на 98,57% залежить від перерахованих
витрат) та
критерієм Фішера F
= 160,766, який більше табличного значення Fтабл = 4,35.
Вплив собівартості на ціну
представлено у вигляді рівняння (6) та у вигляді графіку (2).
(6)
де 
ціна 1,5л. газованої мінеральної води "Регiна", 
собівартість одиниці продукції.
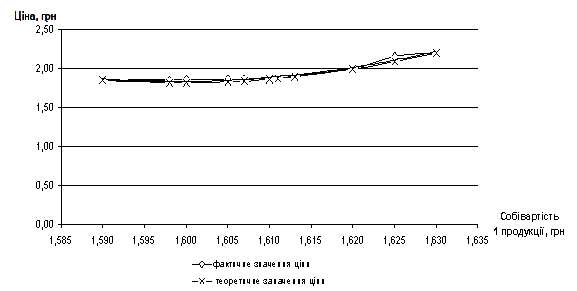
Рис.2. Вплив собівартості на ціну
1,5л. газованої
мінеральної води "Регiна"
Адекватність
побудованого рівняння регресії оцінюється коефіцієнтом множинної кореляції R
= 0,9871 (характеризує тісну
лінійну залежність між собівартістю та ціною), коефіцієнтом детермінації
R2=97,44% (зміна значення ціни на 97,44% залежить від собівартості) та критерієм
Фішера F = 151,541, який більше табличного
значення Fтабл = 5,21.
Регресійний аналіз дозволяє робити
аргументовані висновки щодо розвитку даного економічного процесу, що базуються
та підкріплюються конкретними математичними розрахунками, а також має велике
значення для визначення альтернативи при прийнятті управлінських рішень.
Література:
1. Бідник Н.Б. Використання математичних методів і моделей в економіці,
фінансах. Науковим
вісник НЛТУ України.- 2008. внп. 18.6.- с. 258-262.
2. Вітлінський В.
В. Моделювання економіки: Навч. посібник. -
К.: КНЕУ.-2003. - с. 408
3.
Головатий
М. Ф. Управлінські аспекти соціальної
роботи. Курс лекцій - К.: МАУП.- 2004. - с.368
4.
Прогнозування попиту, основане на методах математичної
статистики // www.students.lviv.ua/index.php?