Экономические науки/8. Математические методы в экономике

Гандура И.И., Грох Н.В.

науковий керівник к.п.н., доц. Клочко О.В.

Вінницький національний аграрний університет, Україна

Оптимальний розподіл капітальних вкладень

Прийняття більшості управлінських рішень ґрунтується на зіставленні очікуваних доходів від певних заходів з витратами, пов’язаними з їх реалізацією. Відомості про види витрат, їх обсяги й динаміка становлять інформаційну базу прийняття рішень щодо формування портфеля замовлень, асортименту продукції, напрямів і обсягів діяльності, управління запасами, ціноутворення, оцінки капітальних вкладень тощо. Стратегія економічного зростання України та її регіонів передбачає проведення на інноваційній основі глибоких структурних перетворень в економіці країни, формування ринкового середовища на засадах конкурентних відносин у всіх сферах економічної діяльності, що вимагає відповідних капітальних вкладень.

Усі економічні процеси та явища є динамічними, оскільки функціонують і розвиваються не лише у просторі, а й у часі. Народне господарство, його галузі, регіони чи окремі підприємства мають розробляти стратегічні і тактичні плани. Перші визначаються з допомогою динамічних моделей, розв'язки яких знаходять методами динамічного програмування. Зауважимо, що сума оптимальних планів на окремих відрізках планового періоду Т не завжди являє собою план, оптимальний на всьому такому періоді.

Розглянемо задачу оптимального розподілу капітальних вкладень, які можуть бути використані двома способами: з метою розвитку рослинництва або тваринництва. Відомо, що за першого способу отримаємо прибуток , а за другого — .

У такому разі однокрокову задачу можна подати у вигляді:

(10.1.)

за умов

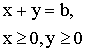, (10.2.)

Нехай

.

Тоді дану задачу можна записати так:

Розглянемо її як задачу оптимального використання капітальних вкладень за окремими інтервалами планового періоду Т, маючи на меті розподілити залишок капітальних вкладень на кінець j-го інтервалу (j= 1, 2, ..., n) двома зазначеними способами. При цьому критерій оптимізації не змінюється: максимізуємо обсяг прибутку за весь плановий період Т.

Якщо на першому інтервалі використано b₁ капітальних вкладень, то на його кінець залишилося їх:

де c, d — коефіцієнти пропорційності, що характеризують використання капітальних вкладень першим і другим способами:

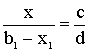
Задачу для другого інтервалу подамо так:

Z₂=g(x)+h(b₂-x₂)

за умов

.

Звідси для будь-якого j-го інтервалу маємо:

за умов

Загальна задача набирає вигляду:

(10.3.)

за умов

,

Отже, у даній роботі представлено оптимізаційні моделі капітальних вкладень регіонального розвитку, які базуються на використанні загальнонаукових та філософських законів і підходів; передбачають врахування ієрархічних цілей розвитку суспільно-територіальних систем та узгодженість рішень на міжрегіональному рівні, врахуванні умов формування капітальних вкладеньного клімату та постановку і досягнення певних цілей на кожному етапі розвитку. Це дає можливість уточнити зміст моделей капітальних вкладень регіонального розвитку, їх структуру, етапи та підходи розробки та можливості застосування в практиці регіонального управління. На сучасному етапі економічного розвитку України розробку моделей капітальних вкладень доцільно здійснювати на основі наукової методології передбачення розвитку процесів капітальних вкладень в регіоні, адаптації до загальних цілей розвитку регіону і держави загалом, до змін клімату капітальних вкладень.

Література:

1. Барковський В., Барковська Н. Математика для економіста. Т. 1-3. ‑ К., 1997.

2. М. Бугір. Математика для економістів. – Тернопіль, 1998.

3. Мельник М.І. Категоріальні засади регіонального капітальних вкладеньного ринку // Науковий вісник Чернівецького торговельно-економічного інституту КНТЕУ: Вип.ІІІ. Економічні науки. – Чернівці: АНТ Лтд., 2004. – С.35-46.

4. Пухир С.Т., Мельник М.І. Перспективні напрямки підвищення капітальних вкладеньного потенціалу регіону (на матеріалах Львівської області) // Наукові записки (Науково-технічний збірник Української академії друкарства). Вип.7. – Львів, 2004. – С.112-117.

5. Ніколаєва О.Г. Математичні методи ринкової економіки. Навчально-методичний посібник. - Харків: ХДТУБА, 2005. – 115 с.