Садыков
В.М., Черненко С.В.
Автомобильно-дорожный
институт ГВУЗ «ДонНТУ»
Применение настраиваемых моделей в контуре управления экономических
систем
Функционирование реальных
систем характеризуется действием неконтролируемых факторов и наличием
неопределенности в наших знаниях о свойствах управляемой системы и среды. Это
требует дальнейшего совершенствования математических моделей, развития теории и
техники идентификации систем в условиях неопределенности по статистическим
критериям. Обусловлено это тем, что во взаимодействии любой системы и среды
всегда содержатся неконтролируемые составляющие, индивидуальные проявления
которых нельзя ни измерить, ни предсказать заранее, так как нельзя полностью
охватить все взаимосвязи явлений и избавиться от случайных возмущений и ошибок
измерений.
Задачи
идентификации возникают так же при создании различных адаптивных систем
управления и технологических процессов, в которых на основе идентификации
объекта вырабатываются оптимальные управляющие воздействия и др.
Крупнейшие достижения в данной области
связаны с работами таких выдающихся ученых, как Аока М., Гроп Д., Дейч A.M., Медич Дж., Мелс Дж., Райбман
Р.С., Сейдж Э., Цыпкин Я.З., Эйкхофф П. [1] и др.
В современной
теории динамических систем выбор структуры объектов испытаний определяется, как
правило, структурой настраиваемой модели, которая описывается уравнениями,
описывающими основные закономерности объекта, либо соотношениями, содержащими
измеряемые входные и выходные величины, характеризующие состояния динамического
объекта. Степень сложности и полноты применяемых моделей определяется
конкретными задачами исследований, а также той априорной информацией, которая
нам известна об объекте, К этой априорной информации относится: порядок
дифференциальных уравнений, описывающих процессы управления, случайных
возмущений и состояния системы, точки приложения помех, длительность временных
характеристик объекта и многое другое [1].
Структурная схема
включения настраиваемой модели в контур управления экономической системы
приведена на рис.1.
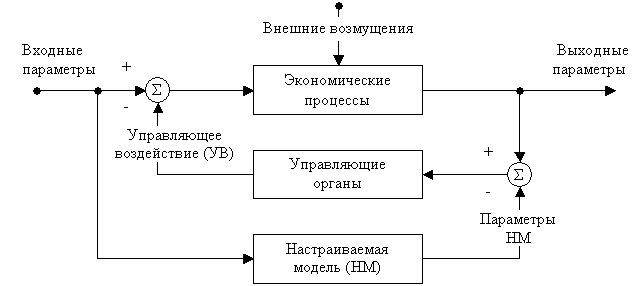

Рисунок 1 –
Настраиваемая модель в контуре управления
Данная схема
обеспечивает неизменность динамических характеристик системы в целом при
изменении динамических характеристик объекта в процессе изменений окружающей
среды.
Например, при
реализации инвестиционного проекта проектируется новый уникальный бизнес-план.
Необходимо, с точки зрения администрации, обеспечить компанию неизменной
управляемостью при всех условиях, возникающих во время бизнес-процесса. В этом
случае передаточная функция настраиваемой модели выбирается так, чтобы она была
оптимальной при неоптимальных реальных процессах. Выходная информация системы
сравнивается с параметрами, получаемыми с помощью настраиваемой модели.
Разность между ними вводится в цепь отрицательной обратной связи, после чего
производится корректировка управляющих действий [2, 322].
Перспективным
является применение настраиваемых моделей, связанное с использованием их для
прогнозирования поведения системы при заданных возмущениях и различных законах
управления, что позволяет отобрать оптимальные варианты управления [3]. Для
этой цели могут быть применены двушкальные системы (рис. 2), где органы
управления и модели отнесены к, так называемой, быстрой части системы. В
быстрой части производится выбор альтернативных вариантов бизнес-планов, анализ
рисков. Модели работают в режиме периодического решения задачи управления в
ускоренном масштабе времени. Анализ всех вариантов должен быть выполнен за
время, не превышающее период дискретности, поэтому появляются дополнительные
требования к времени моделирования [2, 323].
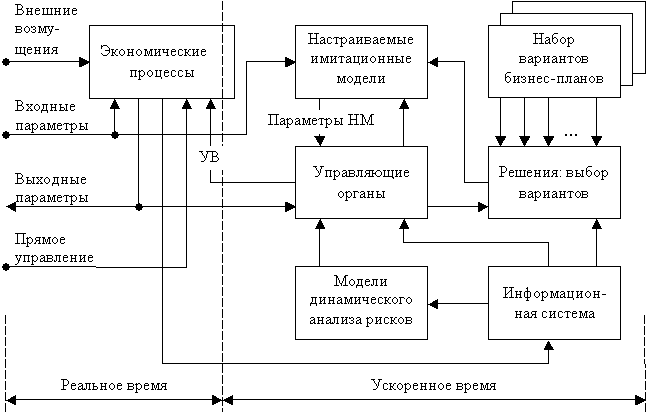

Рисунок 2 –
Двушкальная система с настраиваемой моделью
Двушкальные
системы способны работать с заведомо неточными (относительно прогнозирования)
моделями объектов. В частности, это позволяет применять модель не выше второго
порядка для объектов высокого порядка. Обычно под моделью в такой системе
понимается не одна, а комплекс моделей. Причем для прогнозирования зачастую не
хватает доступного (известного) математического аппарата и поэтому используется
имитационное моделирование с CASE-технологией, ускоряющей создание и
модернизацию моделей [1].
Рассмотренные выше возможности
анализа экономических систем с применением настраиваемых моделей позволяют
использовать кибернетические подходы для оценки свойств экономических
процессов: управляемости, устойчивости, достижимости. Анализ этих свойств
(особенно устойчивости) позволяет более объективно подойти к определению
параметров различных бизнес-проектов с учетом рисковых ситуаций. При этом
включение настраиваемых имитационных моделей в контур управления экономической
системой позволяет качественно улучшить процесс принятия решений и сократить
время прогнозирования.
Литература.