Садыков
В.М., Черненко С.В.
Автомобильно-дорожный
институт ГВУЗ «ДонНТУ»
Моделирование
динамики рыночных цен с помощью паутинообразных моделей
Проблема прогнозирования
равновесной рыночной цены является одной из важных и наиболее сложных в
экономической теории. Классическим
и наиболее распространенным методом поиска ценового равновесия на рынке
является анализ кривых спроса и предложения. Суть его заключается в анализе
кривых спроса и предложения, для нахождения точки рыночного равновесия. Однако
достижение точки равновесия еще не гарантирует устойчивости, в действительности
само равновесие является исключением из правил. Чаще всего наблюдаются
колебания уровня цен и объемов выпуска продукции. Таким образом, равновесная
точка постоянно находится в подвижном состоянии, и статические графики
оказываются бесполезными при составлении прогнозов.
Некоторым образом данную проблему
позволяют решить, так называемые, паутинообразные модели. В общем виде паутинообразная
модель – это динамическая модель ценообразования, которая описывает траекторию
корректировки цен и объема производства при движении от одного состояния
равновесия к другому [1].
За последние два десятилетия паутинообразные модели
претерпели значительных изменений. Сейчас анализируются нелинейные случаи, с
возникающей рыночной нестабильностью и хаосом. Наиболее известными ученными,
ведущими разработки с паутинообразными моделями, являются:
К. Шиарелла, К. Г. Гомес, Б. Финкендштат, А. Матсумото и другие. Среди
отечественных исследователей можно выделить Чумаченко Н. В.,
Лысенко А. И., Шевченко В. В., Боровскую Т. М. и других.
Классическая модель является детерминированной и достаточно
примитивна для переноса на действительный рынок. Поэтому были разработаны
другие, более сложные, паутинообразные модели. Наиболее широкое применение
получили паутинообразные модели с запаздыванием спроса и с запаздыванием
предложения. В первой модели основной идеей является предположение о том, что
спрос в прогнозируемом периоде зависит от предложения товара в предыдущем. Во
второй – наоборот, товаропроизводитель рассчитывает объемы предложения товара
на основе его прошлого спроса. Так реализацию последней модели в объем виде
можно представить с помощью блок-схемы (рис. 1).
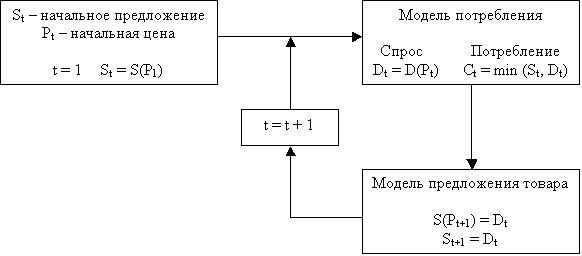

Рисунок 1 – Блок-схема реализации паутинообразной модели с
запаздыванием предложения
Отдельным
направлением в анализе паутинообразной модели ценообразования является
исследование ее хаотического поведения, состояний, при которых возникают
бифуркационные колебания цен.
Так паутинообразную модель
можно рассматривать как дискретную нелинейную систему. Как известно [2], такие
системы подвержены хаотическому поведению при определенных параметрах. Такие
системы являются очень чувствительными к начальным условиям. Чувствительность
от начальных условий значит, что даже сколь угодно близкие траектории с
течением времени расходятся на конечное расстояние, то есть прогноз траектории
на длительное время оказывается невозможен. При этом каждая траектория остается
ограниченной, что противоречит интуитивному пониманию неустойчивости,
основанному на опыте работы с линейными системами [3]. На рис. 2 изображен
пример паутинообразной модели, в которой в качестве кривых спроса и предложения
были выбраны нелинейные (квадратичные) функции.
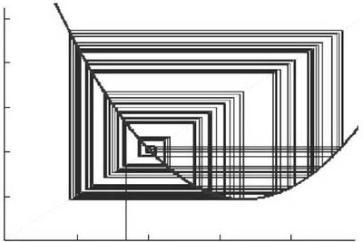
Рисунок 2 – паутинообразная
модель с нелинейными функциями
спроса и предложения
Хаотическое движение
описывается странными аттракторами, которые очень сложны и имеют много
параметров. Странные аттракторы появляются в как в непрерывных динамических
системах (типа системы Лоренца), так и в дискретных (например, отображения
Хенона). Некоторые дискретные динамические системы названы системами Жулиа по
происхождению. И странные аттракторы и системы Жулиа имеют типичную
рекурсивную, фрактальную структуру. Теорема Пуанкаре–Бендиксона доказывает, что
странный аттрактор может возникнуть в непрерывной динамической системе, только
если она имеет три или больше измерений. Однако это ограничение не работает для
дискретных динамических систем. Дискретные двух- и даже одномерные системы
могут иметь странные аттракторы [3], [4].
Такая интерпретация
паутинообразной модели позволяет максимально приблизить ее к действительности.
При этом методы преобразования хаотического движения в периодическое, которые
сейчас активно разрабатываются учеными всего мира [5], предоставляют
возможность разработки стратегий регулирования и стабилизации цен на рынке с
учетом множества, как внешних, так и внутренних факторов.
Сегодня
изучение паутинообразной модели ушло далеко вперед от ее классического
представления. Эта модель позволяет познать внутренний механизм
ценообразования, определить основные параметры, влияющие на систему, и
проанализировать ее поведение. Сейчас это не просто экономическая модель – это
сложный математический анализ, позволяющий объяснить достаточно сложный и не до
конца изученный, процесс изменения цены и вывести схему корректного управления
ценами на рынке.
Литература
- Лебедев В.В. Компьютерное моделирование рыночных
механизмов. http://vivovoco.ibmh.msk.su/VV/JOURNAL/NATURE/12_01/MODEC.HTM
- Боровская Т.М. Моделювання і оптимізація процесів
розвитку виробничих систем з урахуванням використання зовнішніх ресурсів
та ефектів освоєння.
http://universum.vinnica.ua/txt/BorovskaModelOptProcesivVyrobSystem.pdf
- Теория хаоса. Материал из Википедии. http://ru.wikipedia.org/wiki/Теория_хаоса.
- Кроновер Р.М. Фракталы и хаос в динамических
системах. Основы теории. Москва: Постмаркет, - 2000. - 352 с.
- Моспан А.А. Назарова И.А. Моделирование динамики рыночных цен на базе
паутинообразной модели ценообразования. http://masters.donntu.edu.ua/2010/fknt/mospan/diss/index.htm