УДК 746 Системно - структурное моделирование конструкций головных уборов

к.т.н. профессор. Инкаров Б. Г.

Жатканбаева Ж. Н, преподаватель.

Калабергенова Г. Ш, преподаватель.

Академия Дизайна и Технологий «Сымбат»

Известно, какое важное значение имеют головные уборы в одежде

человека [1,-.3,-5]. Системный подход к рассмотрению костюма позволят нагляднее продемонстрировать роль головного убора в нем. Положение головного убора (на голове, а не в руках, как это было в XVII в.) в вертикально развивающейся системе форм логично завершает, уравновешивает или усиливает это развитие вверх. Следует иметь в виду, что костюм уже с XVI в. является многослойным, каждый его слой состоит из частей одежды, облегающих соответственные части тела человека. Женский костюм складывается из верхней одежды и соответствующей ей по характеру шляпы, следующий слой — платье и чепец, который носили под шляпой, дальше — рубашка, к которой на ночь надевали ночной чепец (мужчины — ночной колпак). И в каждом слое одежды головной убор согласуется (адаптирует) с основной частью одежды не только по величине и характеру форм, но и по материалу, цвету, отделке. Головные уборы завершали систему форм костюма в каждом его слое.

Целью настоящей статьи является математическое моделирование конструкций головных уборов с использованием графового принципа построения подсистемы (головного бора).

Считаем, что головной убор как целое состоит из следующих составных частей: макушечная часть, затылочная часть, лобная часть, височная часть [1,-3].

Введем следующие обозначения:

Х₁ → макушечная часть;

Х₂ → затылочная часть;

Х ₃ → лобная часть;

Х₄ → височная часть;

Х₅→ поля;

Представим каждую часть более подробно. В частности имеем, что Х₁ (макушечная часть) может быть:

Х_1.1→ в виде круга;

Х_1.2 → в виде эллипсоида;

Х_1.3→ в виде прямоугольника;

Х_2. → может быть;

Х_2.1→ в виде эллипсоида;

Х_2.2→ в виде плоского эллипса;

Х_3. → может быть:

Х_3.1→ в виде части эллипса;

Х_3.2→ в виде прямоугольника; с козырьком;

Х_3.3→ тоже без козырька;

Х_4. → может быть:

Х_4.1→ в виде части окружности, направленной вверх;

Х_4.2→ в виде части эллипса; направленной вверх;

Х_4.3→ в виде части конуса, направленной вверх;

Х_4.4→ в виде удлиненной цилиндрической части, направленной вверх;

Х_4.5→ в виде плоского удлинения, направленного вниз;

Х_5. → может быть:

Х_5.1→ без полей;

Х_5.2. → с полями в виде части эллипса;

Независимо от того какая конкретно рассматривается система, всегда можно утверждать, что для её описания можно указать конечное число характеристик и параметров системы [4]. Характеристику систем обозначим через Х. Тогда имеем Х= {Х_1, Х_2, Х _3, Х_4, Х_5.}, где Х – вектор характеристик системы; Х_1, Х_1.2, Х _1.3, Х_1.4, Х_1.5.- различные качественные характеристики системы, являющиеся составляющими вектора Х , Здесь Х_1, Х_2, Х _3, Х_4, Х₅ называются компонентами системы. Причем Х не связано с направлением, а означает только то, что система может иметь n характеристик. В нашем случае n равно пяти.

Х_1.1, Х_1.2, и.т.д. это элементы качественных характеристик Х₁, Х_2.1, Х_{2.2 …,} элементы характеристик Х₂. Аналогично имеем, где Х_3, Х_4, Х_5. Таким образом, каждая характеристика Х _J может иметь разные состояния и представлены виде таблице 1.

Таблице 1- Отобразим все состояния в виде таблицы:

Х1	Х2	Х3	Х4	Х5
Х1.1	Х2.1	Х3.1	Х4.1	Х5.1
Х1.2	Х2.3	Х3.2	Х4.2	Х5.2
Х1.3			Х4.3
			Х4.4

Соединим выделенные точки по определенному правилу, используя метод направленных графов. Для получения графа необходимо каждую точку предыдущих множеств соединить со всеми точками последующего подмножества, точки же одного подмножества между собой соединять нельзя. Полученный граф называем упорядоченным ориентированным. В нем можно менять местами число как сами множество Х_1, Х_{2 ,} Х _{3 ,} Х_4, Х₅, так и их элементы (вершины точек). Каждая пара вершин соседних множеств Х_1, Х₂ …, соединяется линией, которая называется дугой графа. Нас интересуют только пути от миноранты до мажоранты на графе. Два пути называется независимыми, если они отличаются хотя бы одной дугой. Следует отметить, что число независимых путей на ориентированном графе равно произведению числа элементов в подмножестве Х_J , где J= к1…, n. Каждый путь на графе G от миноранты до мажоранты может отобразить характеристику какой – либо системы, т.е. М_{J ,} Є, М(G) , где М(G) – множество путей на графе.

Для достижения вполне определенной цели необходимо определенную часть характеристик менять по определенному алгоритму. Это подмножество характеристик назовем управляемым и обозначим R т.е . R= {Х_1.1, Х_1..2 …, Х_2.1, Х_2.2…, Х _3.1, Х _3.2…, Х_4.1, Х_4.2., Х_5.1, Х_5..2.}, где Х_1.1, Х_1..2 …, Х _3.1, Х _3.2…, Х_4.1, Х _5.1, Х _5.2 управляемые характеристики. Таким образом, каждая характеристика V_J имеет конечное число сложений, т.е Х_j ={ Х_{J .1,} Xj.₂…,Xjn}, где J – индекс характеристики n – число дискретных состояний характеристики. Переменные Х_j отобразим на квазиупорядочный граф G = (Х_,Г).

Представим граф в следующем виде:

Х_1.1 Х_2.1 Х_3.1 Х_4.1 Х _5.1

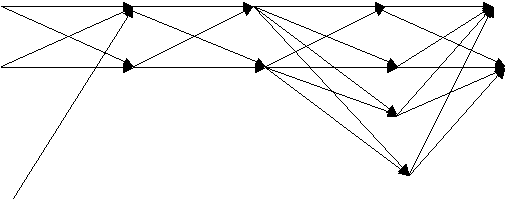
Х _1.2 Х _2.2 Х _3.2 Х _4.2 Х_5.2

Х_4.3

Х_4.4

Х_1.3 Общее количества вариантов равно: N ₌ 3* 2* 2* 4*2= 96.

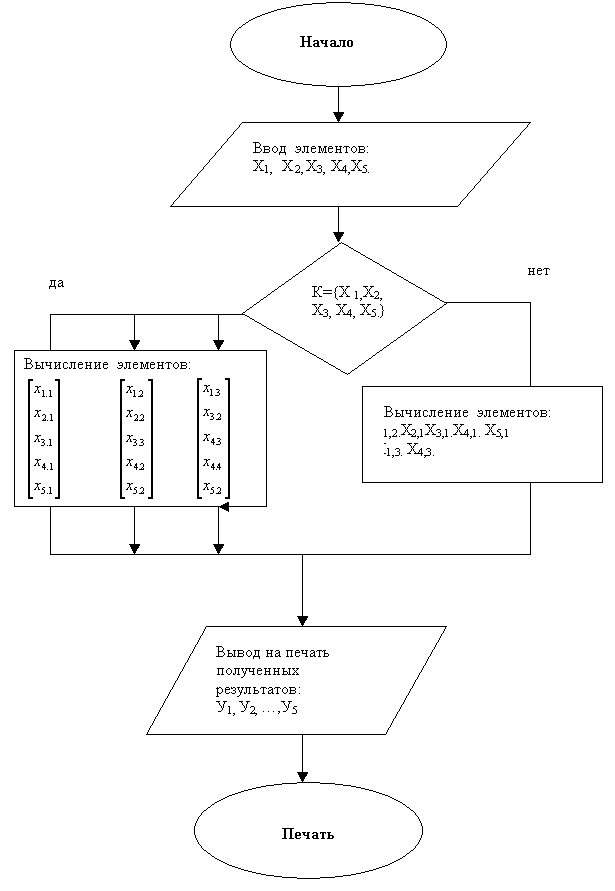
Блок схема проектирования конструкций головных уборов.

_.

Х _1.2 = f ₁(Р₁)

Х _2.1 = f ₂(Р₂)

Х _3.1 = f ₃(Р₃)

Х _4.1 = f ₄(Р₄)

Х _5.1 = f ₅(Р₅)

Х _1.3 = f ₆(Р₆)

Х _4.3 = f ₇(Р₇)

f1 = {Х1.1; Х1.2; Х2.1; Х4.1 }− Береты f 2 = { Х1.1; Х1.3; Х3.1; Х4.2}− Пилотки. f 5 = { Х1.1; Х2.1; Х3.2; Х4.1} − Кубанки. f6 = { Х1.1; Х1.1; Х3.1; Х4.2}− Шляпы

f= {Х1.1; Х2.1; Х3.1;Х4.3} −Ушанки. f4 = {Х1.1; Х2.1; Х3.1; Х4.4 }− Кепки f7 = {Х1.1; Х2.1; Х3..2; Х4.3 }−Конусообразный бoрик , f8 = {Х1.1; Х2.1; Х 3.2; Х4.4 }− Панамки

_{и.т. д., всего N = 96.}

На основании изложенного можно сделать следующие выводы:

1. Математическая модель конструкций головных уборов позволяет получить множество конструктивных решений на основе выбора различных вариантов основных характеристик системы и их состояний.

2. Выбор состояний основных характеристик зависит как от функционального назначения основных элементов, так и от изобретательности и творческого подхода к их выбору разработчиком.

3. Выбор конкретного конструктивного решения зависит от функций цели и выбранного критерия оптимальности. Зачастую критерием выбора является функциональное назначение, соответствующее назначению изделия, её оригинальность, соответствие направлению моды, простата изготовления, низкая себестоимость.

4. Математическое моделирование создает предпосылки для разработки программного обеспечения и перехода на автоматизированный процесс конструирования головных уборов.

Литература:

1.Рытвинская Л.Б., Смородина И.Г., Меркулова Л.А. Проектирование и производство головных уборов. Легпромбытиздат.1987г.

2.Рытвинская Л.Б. Художественное проектирование головных уборов. М ., 1987г.

3.Булатова Е.Б. Моделирование и конструирование головных уборов. М. Альфа 2007г

4. Инкаров Б.Г. Разработка научных основ системного проектирования и методов расчета машин производства кожи и меха из кожи. Автореферат докторской диссертации. Алматы 2009г.

5. Рытвинская Л.Б. Художественное проектирование головных уборов. М., Альфа 2005г

Аннотация

В работе представлена математическая модель создания конструкций головных уборов с использованием теории графов. Получены множество вариантов, позволяющих удовлетворить требования по различным показателям, предъявляемым к изделию. Использование математического моделирования и творческого подхода к выбору геометрии элементов системы создают предпосылки для разработки конструкций, обладающих новизной и оригинальностью.