УДК 517.95

Турметов Б.Х., Шыналиев К.М.

О разрешимости одной краевой задачи для уравнения Лапласа

в круге.

В настоящей работе исследуются вопросы разрешимости одной краевой задачи для уравнения Лапласа. В качестве граничных операторов рассматриваются операторы дробного порядка.

Пусть . Рассмотрим следующие операторы

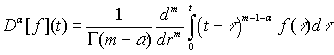
Оператор - называется оператором дифференцирования порядка в смысле Римана –Лиувилля, а - оператором дифференцирования порядка в смысле Капуто (см.[1]).

Пусть .

Введем обозначения

,

.

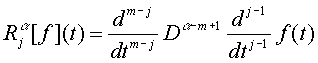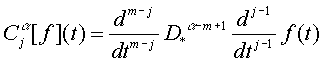Легко показать, что между операторами и имеются следующий связь

. . .

.

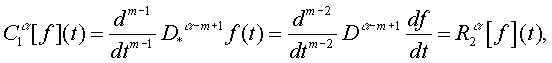
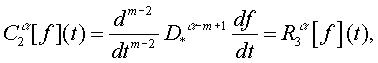
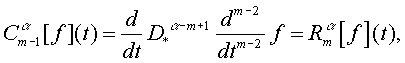
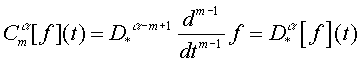Положим и введем оператор

, .

Пусть - единичный круг.Рассмотрим в области следующую краевую задачу

(1)

, (2)

где . ,- фиксированное число, принимающее один из значении , 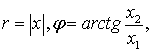и оператор действует по направлению вектора нормали .

Решением задачи (1), (2) назовем гармоническую в области функцию из класса для которой и удовлетворяющий условию (2) в классическом смысле.

Отметим, что краевая задача (1),(2) в случае и соответственно рассматривались в работах [2,3].

Справедливо следующее утверждение.

Теорема. Пусть , и . Тогда

a) если , то решение задачи (1), (2) существует и единственно;

b) если , то для разрешимости задачи (1), (2) необходимо и достаточно выполнения условия

, .

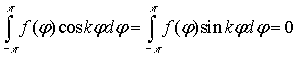Если решение задачи (1),(2)существует, то оно единственно с точностью до полиномов вида

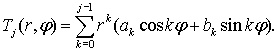
где - произвольные постоянные.

Литература

1. Нахушев А.М. Элементы дробного исчисления и их применения. Иальчик: изд. КБНЦ. РАИ, 2000, 299 с.

2. Турметов Б.Х. Об одной краевой задаче для гармонического уравнения. //Дифференциальные уравнения. Минск 1996.т.32.№8.С.1089-1092

3. Турметов Б.Х. О гладкости решения одной краевой задачи с граничным оператором дробного порядка // Математические труды, 2004. – Т.7, №1, Новосибирск, Изд-во Института математики, С.189-199.