Математика/5. Математическое моделирование
магистрант Оразбаев А.Б., д.т.н., проф. Умралиев
Б.Т.
Атырауский
институт нефти и газа, Республика Казахстан
Анализ математических методов рационального размещения скважин на
залежах нефти и газа
К настоящему времени имеется огромное
количество теоретических работ посвященных проблеме рационального размещения
вертикальных и горизонтальных скважин. В соответствие с общепринятыми
критериями разработки неоднородных залежей, скважины размещаются в зонах с
благоприятной проницаемостью и максимальной мощностью продуктивного пласта
[1,2]. Для оценки эффективности варианта размещения скважин во многих работах использовался коэффициент
нефтегазоотдачи [3,4].
В 70-80 годы прошлого века был разработан
подход к оптимизации размещения скважин, основанный на использовании матрицы
коэффициентов взаимовлияния скважин [5,6]. Этот подход базируется на принципе
суперпозиции (наложения), согласно которому понижение давления, на каком либо
участке площади нефтегазоносности складывается из суммы понижений давления, возникающих
за счет работы скважин, расположенных на всех участках залежи. Это означает, что подход использовал
допущение о линейности уравнения фильтрации газа. В зависимости от характера
решаемой задачи подход реализуется двумя классами методов: статическими и
динамическими методами. В первом случае решается квазилинейная задача, т.е. в
каждый рассматриваемый момент времени учитывается влияние только текущих дебитов скважин; во втором,
помимо этого, учитывается работа скважин за весь предшествующий период. При
оптимизации размещения скважин в качестве критерия оптимальности применялись
минимум скважин или затрат на их строительство, минимум потерь пластовой
энергии.
Для нахождения матриц коэффициентов
взаимовлияния использовались конечно-разностные схемы и электроаналоговые
модели пласта. Исходная информационная задача сводилась к задаче смешанного
целочисленного программирования [7]. Один из оригинальных методов поиска
оптимального размещения эксплутационных скважин по площади залежи был предложен
в работе [8]. В этой работе предложен приближенный подход, который заключается
в выделении для каждой скважины одинаковых удельных объемов дренирования пласта или объемов, пропорциональных дебитам
скважин. Для расчета прогнозных показателей рассматривалась комплексная
геолого-математическая модель [9]. При компьютерной реализации этой модели
пласта использовалась сеточная аппроксимация газовой залежи, точность решения
которой зависит от величины шагов по координатным осям.
Задачу выбора
рационального размещения скважин можно решать методом направленного перебора
наилучшего варианта среди различных вариантов регулярных расстановок скважин.
Отбор производиться по таким показателям, как динамика дебита жидкости и
динамика коэффициентов извлечения нефти или газа (КИН и КИГ, соответственно)
для расчетных вариантов. Для анализа эффективности текущей расстановки скважины
применялись аналитические решения, электроаналоговые модели пласта, физические
модели и конечно-разностные двух- и трехмерные модели [10]. Подобный подход
широко распространен в отечественном проектировании РНМ. Его основным
недостатком является то, что, по сути дела, выбирается вариант размещения из
заранее предложенного множества. Поэтому эффективность такого подхода зависит
от того, насколько эффективны варианты, включенные в это исходное
множество.
В работе [11] процесс
РНМ рассмотрен системой неравномерно расположенных скважин. Модели и алгоритмы,
приведенные в этой работе, позволяют рассчитать выходные показатели процесса
разработки (объема добычи) для «любой» схемы размещения скважин. В работе
применялась электроаналоговая модель.
Однако следует учесть, что в рассматриваемой работе не определяется
рациональное размещение скважин. Таким образом, только для заданной заранее
схемы расстановки можно рассчитать показатели эффективности, поэтому для поиска
более рационального варианта может потребоваться перебор огромного числа вариантов.
Известен алгоритм,
который позволяет автоматизировать процесс ввода и размещения скважин с
элементами оптимизации для реальных моделей пласта [12]. Данный алгоритм
базируется на системе приоритетов скважин и процедуре их упорядоченного
перебора. Ввод скважин в эксплуатацию определяется системой заранее заданных
приоритетов. Например, в пределах одного приоритета ввод скважин производится в
порядке убывания потенциального дебита. Таким способом достигается
первоочередной ввод в разработку зон с более высокой продуктивностью. Таким
образом, оптимизации подвергается не размещение скважин, а их ввод.
Большинство зарубежных
исследователей в своих трудах [13-15] при формировании оптимальных схем
размещения скважин используют разновидности метод случайного поиска, основанные
на генетическом алгоритме. В последних работах были улучшены алгоритмы поиска
расположения скважин с помощью дополнительных алгоритмов и оптимизационных
методов, которые работают вместе с генетическим алгоритмом (ГА). Например,
Гюягулер и Хорн [13,14] оптимизировали расположение скважин с позиций
максимизации чистого дисконтированного дохода. Авторами использовались
гибридный ГА вместе с алгоритмом многоугольника. Чтобы сократить число запусков
гидродинамической модели пласта были применены нейронные сети и крайкинг.
Биттенкурт и Хорн [15] использовали аналогичную технику, комбинируя ГА с другим
методом поисковой оптимизации.
Для решения задачи
оптимизации размещения ограниченного числа разведочных скважин, в работе [16]
применяется дискретный алгоритм оптимизации супермодулярной функции на решетке
кубов. Однако при размещении эксплуатационных скважин необходимо, кроме
геометрических характеристик, использовать и данные о продуктивности участков
пласта.
В работе [17] задача
оптимизации размещения скважин решается на основе двухмерной площадной модели
однофазной фильтрации газа при газовом режиме. Решение задачи по сути дела
сводится к поиску расстояний между скважинами при их заданной схеме размещения,
что снижает ценность предлагаемого подхода. В работе [18] предлагается общий
подход к решению задач размещения объектов сбора и переработки распределенного
ресурса, к которым можно отнести и объекты добычи нефти и газа. Подход основан
на многокритериальном анализе решений, сгенерированных с помощью
многовариантных расчетов.
В работе [19]
одновременно решается задача размещения и управления дебитами нефтяных скважин
с помощью богатого арсенала численных методов конечномерной оптимизации.
Рассматривается расстановка нагнетательных скважин, а также используется
горизонтальный пласт с однофазной фильтрацией нефти, что следует отнести к недостаткам
работы.
Применение для размещения скважин методов
оптимизации рассмотрено в работе [20]. Для этого авторы работы использовали алгоритм линейного частично-целочисленного
программирования. Задача ставиться следующим образом. Дано размещение
некоторого множества скважин на залежи. Пусть число скважин равняется n. Известно желаемая динамика добычи
нефти всей залежи и отдельно для каждой скважины (зависимость суммарной
накопленной добычи от времени). Требуется определить подмножество скважин,
число которых равняется m, где m <
n, которое в наибольшей степени будет
обеспечивать минимальное отклонение от заданной динамики добычи. Математическая
формулировка (модель) задачи имеет вид:
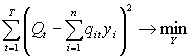 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
где ![]() - требуемый
объем суммарной добычи нефти, газа к моменту времени t;
- требуемый
объем суммарной добычи нефти, газа к моменту времени t; ![]() - объем накопленной
добычи газа к моменту времени t за
счет эксплуатации i-й скважины; n - общий
фонд эксплуатационных скважин; m -
фонд действующих скважин.
- объем накопленной
добычи газа к моменту времени t за
счет эксплуатации i-й скважины; n - общий
фонд эксплуатационных скважин; m -
фонд действующих скважин.
Из приведенной
математической формулировки следует, что осуществляется не рациональное
размещение скважин, а проводиться отбор наиболее приемлемых скважин из
заданного множества. Таким образом, данная модель не отвечает поставленным целям.
В работе [21]
исследователи предложили новую методику размещения морских платформ, основанную
на алгоритме ветвей и границ. В качестве практического применения они приводят
пример разработки шельфового месторождения. При решении задачи рассматривались
различные сценарии, которые значительно сокращают время вычислений.
В работе [22]
предложена методика решения проблемы размещения скважин, учитывающая
неопределенность в пластовых параметрах месторождения. Предлагаемая методика
определяет множество искомых объектов и схему размещения скважин на основе
статической модели коллектора, что используется для отбора начальных вариантов
расстановки скважин. В связи с этим при использовании описанного подхода
необходимо в качестве исходной информации иметь набор вариантов размещения
скважин, формирование которого является самостоятельной и трудоемкой задачей. В
процессе размещение скважин, в первую очередь, генерируется модель коллектора.
Далее производиться расстановка заданного числа скважин на увеличенных сетках
модели коллектора, размеры которых определяются ограничением на межскважинное
расстояние. После чего генерируются варианты конфигурации скважин в пласте с
учетом буровых ограничений на соединение одной или несколько искомых скважин с
платформой.
Авторы работы
[23] использовали крайкинг в виде программы-заменителя (Proxy-model) при
решении многовариантной задачи поиска рационального размещения и определения
режимов работы скважин при проектировании разработки месторождений нефти и
газа. В качестве целевой функции использовался чистый приведенный доход (ЧПД).
Применение крайкинга обеспечила значительного сокращения запусков
гидродинамических программ для вычисления показателей разработки залежи. Однако
использование значительно упрощенных моделей пласта (Proxy-model) может
привести к тому, что не будут учтены факторы, имеющие решающее значение для
размещения скважин.
В работе [24] вводится
понятие «карта качества» пласта, которая представляется двумерным массивом,
элементы которого интегрируют фильтрационно-емкостные свойства фрагментов
неоднородного пласта. Использование предварительно построенной карты качества
пласта позволяет оценить добычные характеристики залежи без запуска симулятора
в процессе оптимизации. Принцип создания карты качества пласта состоит в
следующем. В начале модель пласта разделяется на блоки. Гидродинамические и
геологические параметры блоков отличаются друг от друга, в зависимости от
параметров ячеек модели пласта, которые расположены внутри блоков. Далее
необходимо разместить одну скважину в один из блоков модели пласта и запустить
гидродинамический симулятор для расчета показателей разработки. Затем, после
вычислений, определяются показатели, характеризующие степень извлечения нефти.
Переставляя скважину из блока в блок, и запуская после каждой перестановки
симулятор, формируют массив из показателей добычи, что и будет являться
двумерной картой качества.
Данный метод позволяет
заменить громоздкие гидродинамические вычисления, определяющие фильтрацию
флюидов в пласте, на статические двумерные карты качества. Таким образом, поиск
расположения скважин в пласте не требует вычислительных затрат на многократный
запуск симуляторов для вычисления значений функции цели, а сводиться к работе с
картой-заместителем. Однако требуются многократные запуски симулятора на стадии
формирования карты качества пласта.
Таким образом,
основными достоинствами существующих методик по рациональному размещению
скважин являются:
- использование
симуляторов (пакетов по гидродинамическому моделированию пластовых систем) и
экспертных знаний, что позволяет учесть неоднородность пласта и другие важные
характеристики, участвующие в формировании допустимых вариантов размещения
скважин;
- использование
алгоритмов оптимизации для выбора наилучших вариантов размещения скважин.
Отмеченные достоинства
проанализированных работ будут учтены в предлагаемом ниже подходе к
моделированию процедур рационального размещения скважин.
Основными недостатками
существующих методик по рациональному размещению скважин являются:
- выбор наилучшей
схемы размещения часто сводится к перебору заранее заданных схем, среди которых
не гарантируется наличие варианта размещения, обладающего высокими
технико-экономическими показателями эффективности;
- используемые
алгоритмы оптимизации, в большинстве случаев, требуют многократного обращения
(запуска) симулятора для проведения гидродинамических расчетов и последующего
вычисления значения целевой функции (число таких обращений пропорционально
числу итераций, необходимых алгоритму оптимизации для поиска окончательного
решения);
- генетические
алгоритмы, широко применяемые в известных методиках для рационального
размещению скважин, не гарантируют получение глобального экстремума функции
цели, не позволяют оценить степень приближения к точному решению и обладают
медленной сходимостью к оптимальному решению.
Предлагаемый в данной
магистерской диссертационной работе подход к поиску рационального размещения
скважин направлен на преодоление указанных проблем.
Выводы: Исследованы математические методы
рационального размещения скважин на залежах нефти и газа, рассмотрены проблемы
и подходы к их решению, приведена общая постановка задачи исследования. Анализ
существующих работ по созданию автоматизированных процедур размещения скважин
для месторождений со сложным геологическим строением показал, что эффективность
таких процедур повышается, если они основаны на тесном взаимодействии
гидродинамических и оптимизационных моделей.
Литература:
1. Зотов Г.А., Коротаев Ю.П., Кичиев К.Д. Приближенный
метод расчета работы неравномерной системы скважин в изолированном газовом
пласте. Сб. ВНИИГАЗа, вып. 2, М. Недра, 1965. –С.110-125.
2.
Xpress-Mosel language reference manual (Dash Optimization), 2003.-р.232.
3. Алиев З.С., Сомов Б.Е., Чекушин В.Ф. Обоснование
конструкции горизонтальных и многоствольно-горизонтальных скважин для освоения
нефтяных месторождений. - М.: Техника, 2001. - 192 с.
4. Назыров М.Р., Баишев В.З., Кривина Т.Г., Левина
Н.А. Обоснование и выбор системы
размещения скважин при освоении крупных газоконденсатных месторождений.//
Геология, бурение, разработка и эксплуатация газовых и газоконденсатных
месторождений. Научно-технический сборник. –М.: ИРЦ Газпром, 2001, -№5,
-С..67-73.
5. Закиров С.Н., Зотов Г.А., Маргулов Г.Д., Турниер
В.Н. К оптимизации системы размещения
скважин на площади газоносности // Разработка и эксплуатация газовых и
газоконденсатных месторождений. Реф. сб. - М.: ВНИИЭГазпром, 1972, № 2, -С.3-9.
6. Сенюков Р.В. Оптимизация размещения скважин на газовых
месторождениях. Разработка и эксплуатация газовых и газоконденсатных месторождений.
Научно-технический обзор, М.: ВНИИЭГазпром, 1977. -23 с.
7. Коротаев Ю.П., Умрихин Н.Б. Разработка методов
оптимизации размещения эксплутационных скважин. Разработка и эксплуатация
газовых и газоконденсатных месторождений// Реф. cб. ВНИИЭГазпром, 1975, -№9,
-С.32-35.
8. Колбиков С.В., Губанова Е.Б. О приближенном подходе к
решению задачи размещения эксплуатационных скважин по площади залежи. Сб. тез.
докл. Научно-практической конференции «Проблемы разработки газовых и газоконденсатных
месторождений». Москва, 12-15 ноября, 1998. –С.72.
9. Хачатуров В.Р., Туев С.В. Математические модели и
системы для формирования и оценки стратегий освоения морских месторождений
углеводородов. - М.: ВЦ им. А.А. Дородницына РАН, 2002. -75 с.
10. Панков М.В. Гидродинамическое обоснование рациональных
систем размещения горизонтальных и вертикальных скважин: Дисс. канд. физ.-мат.
наук: 01.02.05 Томск, 1999. -146 с.
11. Минский Е.М., Малых А.С., Пешкин П.А., Фрумсон
Ю.В., Разработка газового месторождения
системами неравномерно расположенных скважин. // Труды ВНИИГАЗ, вып. 34/44, М.:
Недра, 1968. -175 с.
12. Бузина Т.С., Леонтьев И.А., Непомнящий Л.Я., Шеберстов
Е.В.,
Чельцов В.Н. Программный комплекс для проектирования разработки
Астраханского газоконденсатного месторождения.//
Газовая промышленность, 1998, -№1. -С.34-36.
13. Guyaguler B. Optimization of
well placement and assessment of uncertainty. A dissertation for the degree of
doctor of philosophy. Stanford University. 2002.
-137 p.
14.
Guyaguler, В., Home, R. N.,
Rogers, L, and Rosenzweig, J. J. (2002), "Optimization of Well Placement
in a Gulf of Mexico Water flooding Project", SPEREE (June 2002). - Р.229.
15. Bittencourt A. C, Home R.N.
Reservoir development and design optimization. In SPE Annual Technical
Conference and Exhibition, San Antonio, Texas, October 1997. SPE 38895. - Р.14.
16. Комбинаторные методы и алгоритмы решения задач
дискретной оптимизации большой размерности./ В.Р. Хачатуров, В.Е.Веселовский,
А.В. Злотов и др. -М.: Наука, 2000. –360 с.
17. Кричлоу Г.Б. Современная разработка нефтяных
месторождений – проблемы моделирования. -
М.: Недра, 1979. -303 с.
18. Туев С.В.
Математические модели и алгоритмы оптимизации сбора и переработки
распределенного ресурса: Дисс. канд. физ.-мат. наук: 05.13.18 Москва, 2000.
-137 с.
19. Айда-заде К.Р., Багиров А.Г. О задаче размещения нефтяных скважин и управления их дебитами.//
Автоматика и телемеханика, №1, 2006, -С.52-62.
20.
Rosenwald G.W., Green D.W. «A method for determining the optimum location
of wells in reservoir using mixed-integer programming» SPE J., 1973. -р.12.
21.
Garcia-Diaz J.C., Startzman R., Hogg G.L. «A New methodology for minimizing
investment in the development of offshore fields». SPE Production and Facilities,
29, 1996. - Р.8.
22.
Bangerth W., Klie H. Matossian V. «An automatic reservoir framework for
the stochastic optimization of well placement», Center for Subsurface Modeling,
The University of Texas at Austin, 2006. - Р.255-269.
23. Pan Y., Home R.N. Improved
methods for multivariate optimization of field development scheduling and well
placement design. In SPE Annual Technical Conference and Exhibition, New
Orleans, Louisiana, 27-30, September 1998. SPE
49055. - Р.16.
24.
Da Cruz, P. S., Home, R.N., and Deutsch, С.V. The Quality Map: A Tool for Reservoir
Uncertainty Quantification and Decision Making // paper SPE 56578, Houston,
U.S.A., 3-6 October, 1999. - Р.11.