Математика/5. Перспективы информационных

магистрант Калыбаева А.К., д.т.н., проф. Оразбаев Б.Б.

Атырауский институт нефти и газа, Республика Казахстан

Корреляционный алгоритм распознавания контура и алгоритмизация задач утончение объектов

В работе предлагается процедура распознавания контуров изолированных изображений объектов широкого класса, который использует обучающую выборку (ОВ) из элементов (контуров изолированных изображений). Построенная система эффективно распознает изображения из классов, установленных этой обучающей выборкой. Одна из стадий до обучения и распознавания является локализация объекта на области рецептора, т.е. на этой стадии определяется минимальная прямоугольная область , которая полностью содержит объект. Допустим, что при этом выполняются следующие условия.

C.1. Области локализации двух различных объектов не пересекаются.

C.2. Объекты расположены на изображении таким образом, что они условно могут быть разделены линиями.

C.3. Невозможно нарисовать горизонтальную или вертикальную линию в области не пересекающую объект .

Перечислим типы искажений, влияние которых игнорируются для вводимого определения системы.

D.1. Сжатие и растяжение объекта по оси ОХ или оси ОУ;

D.2. Локальное искажение контура объекта в указанных границах;

D.3. Наклон или вращение объекта на указанный угол.

Каждый контур располагается в некоторой области поля рецептора, и определение контура определяется в соответствии c расположением части контура объекта в соответствующей области изображения. Так как ответ системы распознавания должен соответственно отличаться для различных образцов, то каждый контур должен приблизительно располагаться в области изображения, для которой можно выделить существенные различия для разнообразных образцов. При этом необходимо принять во внимание и деформации, допустимые для распознаваемых изображений. Назовем такие области изображений информативными.

Предположим, что относительные допустимые искажения не превышают некоторый порог (1 < < 1) и для всех таких искажений, контуры из разных классов достаточно отличаются друг от друга. Тогда мы делим область локализации объекта на m² (m = [1/]) ячеек с длиной стороны . Мы назовем это разделение -разделением области локализации объекта . Для любого объекта разбиение содержит то же самое количество и местоположение ячеек. Мы будем искать информативные области изображений среди множества ячеек .

Пусть дан объект . Построим ε-разделение области локализации объекта и для каждой клетки установим вес v_ij в зависимости от того, пересекает ли контур объекта его или нет, . Мы получаем матрицу

,

где

Если , то ячейка называется информативной для объекта . Назовем матрицу V_k -образцом объекта .

-образцы V_p и V_q различимы, если для некоторых i и j следующие условия справедливы , и , .

Система -образцов называется делимой, если существуют i и j, для которых условие 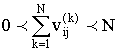справедливо.

Предположим, что мы имеем N ε-образцов, построенных согласно ОВ и таких, что каждые два из них различимы, т.е. для каждого -изображения можно найти такие ячейки , чьи веса отличают его от остальных -образцов.

Рассмотрим матрицу C = , где 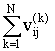, если для всех и в противном случае.

Матрица C имеет следующие свойства:

- только для тех ячеек , которые являются информативными для -образца любого объекта ;

- если , тогда значение c_ij = числу -образцов V_k, для которых (т.е., ячейка пересекается контуром объекта), и значение (N–c_ij) = числу объектов , чьи контуры не пересекают ячейку .

Алгоритм требует выполнения указанных условий, налагаемых на -образцы выборки. Эти условия обеспечиваются итеративным подбором величины . Заметим также, что при слишком маленьком необходимо существенно увеличить ОВ для более точного представления структуры образца. При этом численные проблемы системы увеличиваются, поэтому, операционное время и размер используемой памяти также увеличивается, что уменьшает, в общем, эффективность системы. Поэтому необходимо найти компромисс между выбором и установкой его в зависимости от особенностей множества распознаваемых образцов.

Алгоритм распознавания контуров по идеальным эталонам устанавливает принадлежность неизвестного изображения к определенному классу изображений (образу) на основе корреляционного метода [1]. Объектами распознавания служат плоские контуры объектов. Образы заданы при помощи идеальных эталонов контуров. Каждый контур описывается прямоугольной матрицей из элементов 0,1, где – число ее столбцов, – число строк.

Эталонные матрицы получены следующим способом: четкое изображение знака раскладывалось прямоугольным растром на точек и если в данной точке присутствовал хоть один пиксель изображения, то соответствующему элементу матрицы приписывалось значение «1», в противном случае – значение «0». Идеальные «черно-белые» эталоны удобны с точки зрения экономии памяти при машинной реализации алгоритма распознавания и учете погрешности.

В процессе корреляционного распознавания находится максимум коэффициента корреляции между неизвестным изображением и эталоном по всем сдвигам изображения относительно эталона и по всем эталонам. Если распознаваемые изображения принадлежат алфавиту из контуров, то необходимо иметь минимум эталонов – по одному представителю на каждый контур. Ответом распознавания служит номер эталона, давшего с предъявленным изображением максимальную корреляцию, указанный эталон и является ответом распознавания.

Система обеспечивает высокую скорость процедуры распознавания. Качество распознавания достигается установкой представительной ОВ и выбором соответствующего . Способ установки обеспечивает правильное распознавание объектов, которые написаны с некоторыми искажениями и отклонениями от соответствующих объектов ОВ, и не зависят от их линейных размеров.

Система распознавания была реализована программно и была применена для распознавания. ОВ вводится в базу данных, с помощью которой можно обновлять и исправлять данные.

Коэффициент корреляции двух изображений, представленных векторами и в – мерном фазовом пространстве, вычисляется по формуле

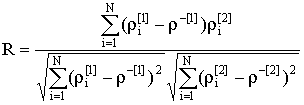, (1)

где , , .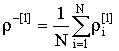

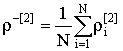В знаменателе выражения (1) находится произведение модулей двух векторов, полученных из и вычитанием соответствующих средних значений и из компонент и .

Рассмотрим вопросы алгоритмизации задач утончение объектов. Утончение полутоновых изображений является более сложным, чем утончение бинарных изображений. В большинстве случаев объекты полутоновых изображений не имеют четких границ и зашумлены аппаратными, точечными шумами. Существует ряд алгоритмов полутонового утончения, которые можно разделить на два класса:

а) утончение только конкретных объектов или областей исходного изображения;

б) все исходное изображение должно быть обработано как область для утончения.

Большинство задач принадлежит второчу классу. Общие требования для результатов утончения полутонового изображения могут быть определены как следующие:

- если объект - связный, то результат должен быть связным;

- утончение не должно менять топологию объекта;

- средняя линия, полученная после утончения, должна проходить через пиксели с наибольшей величиной яркости, т.е. через хребет, если полутоновую величину яркости рассматривать как высоту.

Большинство алгоритмов полутонового утончения являются итерационными, т.е. последовательно удаляются или уменьшаются значения пикселей на границе объекта до тех пор, пока не останется только скелет. Уменьшение или сохранение обрабатываемого пикселя или сохранение пикселя зависит от конфигурации его окрестности.

Алгоритмы утончения можно классифицировать по методу проверки окрестности. Алгоритмы, основанные на использовании принципов полутоновой морфологии или дистанционных преобразований. Абсолютное большинство алгоритмов, основанных на полутоновой морфологии, является обобщением утончения бинарных изображений, а именно: вместо бинарных значений пикселей рассматривается их полутоновая яркость и яркости окружающих его пикселей. Алгоритмы, использующие дистанционное преобразование, анализируют образования из множества областей, имеющих приблизительно одинаковую яркость. В этом случае изображение представляется рядом центров и радиусов максимальных соседей, полностью включенных в эти регионы.

По типу операций алгоритмы утончения разделяются на 2 группы - последовательные и параллельные. В последовательном алгоритме пиксели проверяются в фиксированной последовательности на каждой итерации, и удаление конкретного пикселя зависит от всех операций, которые были выполнены до сих пор, т.е. от результата предыдущей итерацией. В параллельных алгоритмах существует зависимость только от предыдущей итерации, т.е. результаты обработки каждой итерации связаны марковской цепью.

Полутоновое изображение представляется как набор (0,1) изображений, где полутоновая величина является номером бинарного изображения [2]. Основываясь на этом, введем несколько понятий:

- слоем полутонового изображения для определенного уровня является бинарное изображение, в котором значение имеют только пиксели с полутоновой величиной выше или равной этому уровню;

- краям соответствует множество граничных точек в объектах на вышеуказанном бинарном изображении.

Следует отметить, что при обработке одного слоя необходимо рассматривать и слой, лежащий и выше его. И если по очереди проводить бинарную обработку каждого слоя, начиная с верхнего уровня, то результат обработки последнего уровня будет соответствовать результату обработки всего полутонового изображения.

В основе алгоритмов утончения лежит анализ окрестности пикселя и обработка пикселей изображения.

Исключением из этого класса алгоритмов являются алгоритмы, основанные на комбинации отслеживающих алгоритмов с окном и являющиеся с одной стороны итерационными, с другой - фильтрационными. Работа таких алгоритмов заключается в следующем.

Исходными данными алгоритма являются управляющий параметр алгоритма (порог R) и исходное множество S. Алгоритм состоит в следующем:

Шаг 1. Задаются исходное множество допустимых объектов S_iÎS, i=1,..., m, и радиус R гиперсферы.

Шаг 2. Любой объект S_iÎS назначается центром Z₁(1) (эталоном) этой гиперсферы Q₁ и определяются объекты, входящие в гиперсферу, т.е._. S_jÎ Q₁.

Шаг 3. Переопределяется центр гиперсферы как усредненный центр

(2)

объектов, вошедших на предыдущем шаге в гиперсферу через формулу

, где m₁ – число объектов,

попавших в гиперсферу Q₁ ; S_j – объекты гиперсферы Q₁.

Шаг 4. Вновь определяются объекты S_iÎS, для которых, как и на предыдущем шаге,

r (Z₁ (2), S_j)=||Z₁ (2)-S_j||£ R, j=1, 2,..., m.

Шаг 5. Процедуры шагов 3, 4 повторяются до тех пор, пока не перестанут изменяться координаты центра тяжести (усредненного центра). Очевидно, при этом гиперсфера остановится в области одного из локальных максимумов плотности объектов исходного множества S. Гиперсфера с центром Z₁ представляет собой кластер K₁.

Шаг 6. Из исходного множества S исключаются объекты S_jÎK₁, т.е. входящие в кластер K₁. Объекты, через которые гиперсфера проходила на своем пути к конечному положению, к моменту остановки гиперсферы исключаются из нее, сохраняются, т.е. после формирования кластера K₁ исходное множество сокращается на число m₁, т.е. S^¢=S \ S(K₁).

Шаг 7. Если итерация не последняя или множество не распределено по кластерам полностью, процедура построения кластера повторяется с шага 2, в качестве первоначального центра выбирается объект S_iÎS^¢.

Таким образом, процедура выделения кластеров K_j повторяется до тех пор, пока все исходное множество S не будет разделено на кластеры K_j, j=1, 2,..., l, представленные центрами гиперсфер радиуса R. Очевидно, что величина l есть некоторая функция от радиуса R, l=f (R), т.е. в зависимости от величины R получается разное число l.

Выводы: Исследована процедура распознавания контуров изолированных изображений объектов широкого класса. Предложен и описан корреляционный алгоритм распознавания контура, исследованы и решены основные вопросы алгоритмизация задач утончение объектов На основе результатов анализа окрестности пикселя и обработки пикселей изображения предложен эффективный алгоритмов утончения.

Литература:

1. Восприятие (механизмы и модели). М.: Мир, 1994. – 367 с.

2. Кемени Дж., Снелл Дж. Конечные цепи Маркова. М.: Наука,-1980.-271 с.

3. Мустафин С.А. Разработка и исследование математических методов, моделей и алгоритмов распознавания контуров трехмерных объектов//Автореф. диссертации канд. тех.наук. –Алматы: 2007. -23 с.