Математика/5. Математическое моделирование
магистрант Оразбаев А.Б.
Атырауский институт нефти и газа, Республика Казахстан
Формализация и
математическая постановка задачи оптимизации размещения скважин на нефтяной
залежи и методы их решения
Рассмотрим вопросы разработки модели
оптимальной расстановки скважин на нефтегазовой залежи. Под оптимальным
размещением забоев скважин понимается их расположение, которое обеспечивает:
а) как можно меньшее расстояние скважин до
любой точки пласта и примерное равенство областей дренирования скважин, что
направлено на максимально возможный охват пласта заданным количеством скважин;
б) максимально возможное приближение
скважин к блокам, имеющим большие значения эффективности.
Введенное понятие оптимальности
соответствует эвристическим правилам размещения скважин, принятым в практике
разработки нефтяных и газовых скважин. Эти правила направлены на обеспечение
максимального извлечения нефти и газа из пласта. Приведенный набор может быть
дополнен или изменен. Ниже будет формализована количественная оценка
эффективности.
Рассмотрим, прежде всего, модель
размещения, которая применяется в случае, когда залежь представляется двумерной
областью. Следует уточнить, что, в этом случае, размещение скважин равносильно
лишь выбору участка залежи, в котором целесообразно разместить скважину. При
этом не выбирается зона перфорации для вертикальной скважины или положение
горизонтального участка скважины относительно кровли и подошвы пласта. В этом
состоит ограниченность предлагаемых моделей. Однако после выбора участков
(блоков, ячеек), содержащих скважины, можно перейти к поиску наилучшего размещения
скважины внутри участка. Другим ограничением модели является то, что
определяется размещение для заданного числа скважин. Это ограничение можно, в
некоторой степени, обойти, решая задачу несколько раз для нескольких значений
числа скважин.
На содержательном уровне задача
рационального размещения скважин ставится следующим образом: пусть нефтяная
залежь разбита на участки, в каждом из которых возможно размещение забоя
скважины; число размещаемых скважин задано; требуется определить набор
участков, содержащих забои скважин, таким образом, чтобы в максимальной степени
обеспечить выполнение введенного выше понятия оптимальности (пункты а и б).
Перейдем к математической формулировке
задачи размещения скважин. Пусть залежь разбита на блоки (участки). Каждый блок
представляет собой прямоугольную призму. Основания призмы - квадраты, одинаковые
для всех блоков, а высота равняется нефтенасыщенной толщине, которую имеет
пласт на этом участке. Таким образом, залежь покрыта совокупностью одинаковых
квадратов. Предварительно считается, что при размещении скважины в каком-либо
квадрате координаты забоя скважины совпадают с центром этого квадрата.
Максимальное количество блоков и, соответственно, минимальную площадь блока,
можно найти, исходя из минимально допустимого расстояния между скважинами.
Минимально допустимая длина стороны квадрата будет совпадать с этим
расстоянием. Минимальное количество блоков, по крайней мере, должно быть в два
раза больше числа скважин, чтобы были возможны не только тривиальные решения.
Введем
исходные параметры. Пусть s - число добывающих скважин, n - число блоков, n³s³1. Будем считать, что п делится без остатка на s.
Введем вспомогательный параметр k=(n/s)
– 1.
Пусть 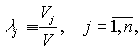 где Vj - геологические запасы j-го блока, Vj³0, а V=max{Vj}>0,
j=
где Vj - геологические запасы j-го блока, Vj³0, а V=max{Vj}>0,
j=![]() . Параметр lj назовем «весом» j-го
блока. В качестве lj можно использовать любой параметр, характеризующий продуктивность
(«важность», «полезность») j-го блока
или потенциальную эффективность скважины, размещенной в этом блоке. В этом
случае оценку lj можно получить, привлекая экспертов, которые могут,
например, учесть «степень опасности» блока с точки зрения его близости к
водоносным горизонтам или учесть расположение геологических разломов. Можно,
например, кроме запасов блока учитывать его проницаемость.
. Параметр lj назовем «весом» j-го
блока. В качестве lj можно использовать любой параметр, характеризующий продуктивность
(«важность», «полезность») j-го блока
или потенциальную эффективность скважины, размещенной в этом блоке. В этом
случае оценку lj можно получить, привлекая экспертов, которые могут,
например, учесть «степень опасности» блока с точки зрения его близости к
водоносным горизонтам или учесть расположение геологических разломов. Можно,
например, кроме запасов блока учитывать его проницаемость.
Тогда, используя «идеологию» метода
анализа иерархий, для оценки lj можно предложить формулу:
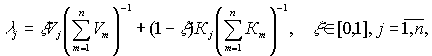 (1)
(1)
где Кj
– абсолютная проницаемость j-го
блока; x - экспертная оценка важности показателя «запасы» по
отношению к показателю «проницаемость», а (1-x), соответственно,
экспертная оценка относительной важности показателя «проницаемость». Если для j-го блока известны его пороговый объем
- Uj, а также начальная и
конечная водонасыщенности, соответственно, w0j, wKj, то
в качестве Vj можно использовать
оценку сверху для извлекаемых запасов: Vj=
Uj(wKj - w0j).
Можно использовать «карту качества» [1]
для расчета lj. В этом случае становится необходимым многократный
запуск симулятора (количество запусков равняется числу блоков), а lj становится нефтеотдачей, которая обеспечивается при
разработке залежи одной скважиной, размещенной в j-м блоке.
Можно в качестве lj использовать экспертную оценку (например, в долях
единицы), выражающую степень приемлемости блока для размещения в нем забоя
скважины (горизонтального участка скважины) [2].
Пусть Rij
- расстояние между центрами i-го и j-го блоков, Rij³0, Rii=0,
R=max{Rij}>0, i=![]() , j=
, j=![]() . Определим параметр сij
– «взвешенное расстояние» между i-м и
j-м блоками:
. Определим параметр сij
– «взвешенное расстояние» между i-м и
j-м блоками:
cij=(lj)(1-g)×(Rij/R)g, gÎ[0,1], i¹j, cij=0,
i=j,
(2)
где g - экспертная оценка важности показателя «расстояние» по
отношению к показателю «вес». Если g=1, то считается, что при размещении скважин следует
учитывать только расстояния между скважинами и участками пласта. Если g=0,
то считается, что размещение скважин устанавливается, только исходя из «веса»
блоков. Параметр cij можно
трактовать, как штраф (или потери) за удаленность скважины, расположенной в i-м блоке, от j-го блока, входящего в область дренирования этой скважины, а {cij} –как матрицу потерь от размещения скважин не во
всех блоках.
Введем
искомые переменные - xij: xij=1, если j-й
блок входит в область влияния (питания) скважины, находящейся в i-м блоке, и xij=0 в ином случае. Из определения xij следует: если в i-м
блоке находится скважина, то xii=1,
в ином случае: xii=0.
С учетом сформулированного выше понятия
оптимальности (пункты а и б) формирование наилучшей схемы размещения скважин
сводится к поиску таких xij,
что
![]() (3)
(3)
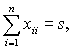 (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Если считать, что все ячейки равноценны по
другим характеристикам, не участвующим в оценке cij, то многокритериальную задачу (3)-(7) можно свести к
однокритериальной модели различными способами. Например, использовать свертку
критериев:
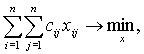 (8)
(8)
или минимаксный обобщенный критерий:
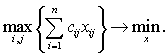 (9)
(9)
Используя известный прием [1], нелинейную задачу дискретной оптимизации (2.9),(2.4)-(2.7) можно
свести к линейной модели, если к ограничениям (2.4)-(2.7) добавить критерий:
x ® min
(10)
и дополнительные ограничения:
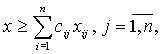 (11)
(11)
где х -
новая дополнительная искомая переменная.
Модель (8),(4)-(7) назовем основной моделью размещения (ОМР). В
этой модели критерий (8) представляет собой минимизацию суммарного штрафа за
размещение скважин не во всех блоках (за удаленность скважин от некоторых
участков пласта). Ограничение (4) - ограничение на число скважин. Ограничение
(5) эквивалентно условию: любой блок может входить только в одну область
дренирования. Ограничение (6) - условие: область дренирования каждой скважины
содержит одинаковое количество блоков [3].
Прежде, чем перейти к обсуждению методов решения полностью целочисленной
задачи или частично-целочисленной задачи воспользуемся результатами
исследования системы ограничений (13)-(16), приведенными в работе [4].
Утверждение
1:
Пусть набор {xij}
удовлетворяет следующим соотношениям:
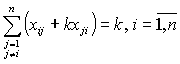 (12)
(12)
![]() (13)
(13)
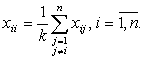 (14)
(14)
Тогда набор {xij} является допустимым решением задач (8), (4)-(7) и
(9), (4)-(7).
Доказательство.
Прежде всего, заметим, что равенство
(14) ведет к выполнению ограничения (6). Далее, из формул (12) следует, что
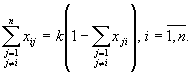
Так как для набора {xij} выполняются условия (13), то сумма, стоящая в
скобках правой части последнего равенства, может принимать только два значения
0 или 1.
Рассмотрим первый возможный случай: 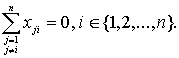
Тогда 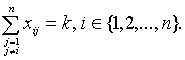 Откуда с учетом
(2.14): xii=1.
Откуда с учетом
(2.14): xii=1.
Поэтому, во-первых,
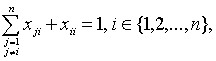 (15)
(15)
что равносильно выполнению (5), и, во-вторых, с учетом
(13) и (15) выполняется (7).
Рассмотрим второй возможный случай: 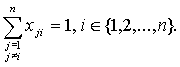
Тогда 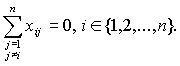
Откуда с учетом (14): xii=0. Поэтому опять выполняется (15), а, следовательно,
и (5). Кроме этого с учетом (13) и (15) выполняется (7).
Итак, выполнение (12)-(14) влечет
выполнение (5)-(7).
Наконец, из выполнения ограничений (5) и
(6) следует, соответственно,
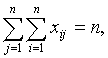
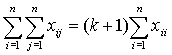
Так как по условию k=n/s-1, то из выполнения
двух последних равенств следует выполнение последнего ограничения (4), что
заканчивает доказательство утверждения 1.
Таким образом, решение задач (8),(4)-(7) и
(10),(11),(4)-(7) можно заменить, соответственно, решением эквивалентных задач
(8),(12), (14) и (10)-(13), имеющих более простую структуру.
Если через {xij*} обозначить оптимальное решение этих
задач, то с учетом (14) xii*
будут вычисляться по формуле:
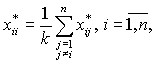
а множество номеров ячеек, содержащих скважины, будут
составлять номера ячеек, для которых xii*=1.
Остановимся на случае, когда п/s
не является целым числом. Чтобы свести этот случай к рассмотренному выше, когда
п/sÎ{1,2,3,…}, можно добавить к уже имеющимся блокам
фиктивные блоки, «вес» которых равняется нулю, а пф - число таких блоков должно быть таким, чтобы выполнялось
условие: (пф+п)/sÎ{1,2,3,…}. После чего решается задача (8),(4)-(7) (или
(8), (12),(13)), в которой количество блоков, на которые разбита залежь, равняется
(пф+п). Однако такой способ не лишен недостатка, а именно, возникает
проблема: к каким участкам залежи должны примыкать фиктивные блоки. Другой
способ связан с видоизменением ограничений (6), которые принимают вид:
![]()
где ]n/s[ - целая часть числа n/s.
Конечно, в этом случае уже неправомерно заменять исходную систему ограничений
(4)-(7) более простыми условиями (12) и (13).
Учитывая формулу (2), которая определяет
формулу для расчета «штрафа» - cij,
можно чуть упростить вид критерия в ОМР, т.е. вместо критерия (8) использовать
критерий следующего вида:
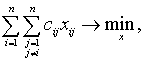 (16)
(16)
Для решения задачи (8),(12),(13) или
(16),(12),(13) можно применить любой стандартный алгоритм линейной дискретной
оптимизации [5]. Решение частично-целочисленной задачи
(10),(11),(4)-(17) можно получить, используя модификацию метода ветвей и
границ, учитывающую «непрерывный» характер переменной х.
К настоящему времени известно множество
разнообразных подходов к решению задач дискретной оптимизации (целочисленного
программирования): методы отсечения, ветвей и границ, алгоритмы направленного
перебора, динамического программирования, случайного поиска и др. На их основе
разработаны точные и приближенные алгоритмы.
Среди точных методов решения задач
целочисленного программирования можно выделить две большие группы: методы,
использующие аппарат непрерывной оптимизации, и комбинаторные методы [6].
Многие методы, относящиеся к первой
группе, базируются на применении дополнительных линейных ограничений -
отсекающих гиперплоскостей. Идея метода отсечения состоит в том, что область
допустимых решений дискретной задачи погружается в некоторое выпуклое
множество, которое последовательно «обрезается» с помощью вводимых линейных
ограничений (отсечений) до получения непрерывной задачи с необходимыми свойствами.
Интенсивная разработка этого метода началась с первого алгоритма Гомори для
решения задач целочисленного линейного программирования [7,8], в котором реализована,
и обоснована схема отсечения, ставшая классической.
Активно развивающимся классом методов дискретной
оптимизации является комбинаторные методы. Общая черта этих методов -
использование ими конечности множества возможных решений и осуществление его
неполного перебора путем отбрасывания некоторых вариантов, заведомо не
приводящих к оптимуму [9]. Основными теоретическими схемами для конструирования
точных комбинаторных методов является схемы последовательного анализа вариантов,
ветвей и границ, динамического программирования. Из комбинаторных методов
наибольшее распространение получил метод ветвей и границ. Метод ветвей и границ
осуществляет направленный перебор допустимых решений и включает выполнение
нескольких основных шагов, позволяющих для большого числа задач существенно
уменьшить число просматриваемых решений. Схема данного метода для случая максимизации
функции на ограниченном исходном множестве G
состоит из следующих стадий:
1)
получение верхней оценки
целевой функции на некотором подмножестве множества G;
2)
разбиение множества G на непересекающиеся подмножества
(ветвление);
3)
пересчет оценок;
4)
получение допустимых
решений;
5)
проверка выполнения
условия оптимальности.
В последнее время активно развиваются
приближенные эвристические алгоритмы решения задач целочисленной оптимизации,
построенные на основе законов эволюции, которым подчиняются процессы,
протекающие в природе. К таким алгоритмам относятся: генетические алгоритмы,
алгоритмы муравьиной колонии, имитации отжига, поиск с запретами и другие [10].
Генетические алгоритмы построены на идее моделирования эволюции природы [11]. В
основе алгоритмов лежит имитация развития популяции живых организмов. Вводится
функция «пригодности», которая определяет качество решения задачи, полученного
на некоторой итерации. Алгоритм сохраняет всю информацию о решении. На каждой
итерации формируются новые решения, замещающие менее «пригодные». Для
построения нового решения выбираются предыдущие решения - «родители» с помощью
вероятностного оператора селекции.
Далее к этим решениям применяются операторы скрещивания
и мутации. Алгоритм заканчивается,
когда проведено заданное число итераций или получено оптимальное
(субоптимальное) решение, которое может соответствовать локальному экстремуму.
Основным недостатком всех эволюционных методов конкретно для решения задач
размещения скважин является необходимость многократного обращения к
гидродинамическому симулятору при определении эффективного варианта расстановки
на каждой итерации, пока не будет найдено наилучшее решение. Это может вызвать
практически неограниченное время, необходимое для поиска оптимального решения.
Следует подчеркнуть основное отличие
предлагаемого подхода по сравнению с существующими методиками
автоматизированного размещения скважин: расчеты по геолого-математическим и
гидродинамическим моделям проводятся один раз на стадии получения исходных
параметров моделей оптимизации. Учитывая продолжительность таких расчетов при
проектировании разработки реальных объектов нефтегазодобычи, а также
значительные затраты времени, сопутствующие решению задач оптимизации большой
размерности, указанное отличие становится важным преимуществом предлагаемого
подхода при практическом использовании методик автоматизированного размещения
скважин.
Отметим также возможность применения
предлагаемых моделей для размещения поисковых (разведочных) скважин. В этом
случае в качестве lj – веса j-го
блока можно использовать вероятность нахождения нефти (газа) в этом блоке.
Остановимся на проблемах применения
предлагаемых моделей при большой размерности задач размещения скважин (большое
число блоков и скважин). Такое исследование является важным, т.к. при большой
размерности задач дискретной оптимизации методы целочисленного программирования
требуют значительных затрат компьютерной памяти и, соответственно, значительного
времени решения. Чтобы снизить негативное влияние большой размерности задачи,
можно воспользоваться методами, приведенными в работе [12], в большей степени,
по сравнению с классическими алгоритмами, ориентированными на решение
дискретных задач оптимизации большой размерности.
Можно предложить дополнительную процедуру
разбиения залежи на зоны меньшей площади. После такого разбиения решается
задача размещения скважин для каждой из полученных зон. Для формализованного
описания процедуры введем обозначения. Пусть n – заданное число блоков, на которые разбита залежь; п0 – допустимое при расчетах
число блоков, которое определяется, исходя из возможностей метода оптимизации, п0<п; s – заданное число
добывающих скважин; s0 -
допустимое при расчетах число скважин, которое определяется, исходя из
возможностей метода оптимизации, s0<s. Введем вспомогательный параметр N0: N0=]п/п0[+1, где через ]x[ обозначена целая часть числа x. Пусть N – количество зон, на которые необходимо разбить залежь. N – параметр, подлежащий определению.
Тогда можно предложить процедуру, состоящей из следующих операций:
1) полагаем N=N0;
2) разбиваем газоносную площадь залежи на N зон одинаковой площади;
3) используя данные геологической модели
залежи, определяем Vl –
балансовые запасы газа l–й зоны, l=![]() ;
;
4) определяем sl - количество скважин в l-й зоне:
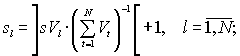
5) проверяем выполнение правила остановки:
если выполняется sl£s0, l=1,…,N, то процедура разбиения на зоны заканчивается; в ином случае следует
положить N=N+1 и вернуться к пункту
2).
После разбиения залежи на меньшие по
площади зоны решается задача размещения для каждой зоны в отдельности, причем
число скважин в l-й зоне равняется sl, l=![]() .
.
Следует отметить, что в первоначальное
множество блоков, составляющих залежь, включаются блоки, для которых балансовые
запасы имеют значения, не меньшие заданной допустимой величины.
Выводы: Формализованы и получены
математические постановки задач оптимизации размещения скважин на нефтяной
залежи и предложены методы их решения. Путем добавления дополнительного критерия
(2.10) и ограничений (2.11) полученная нелинейная задача дискретной оптимизации
сведена к линейной модели. Предложены способы формирования исходных параметров
модели размещения скважин. Показана возможность использования предлагаемого
подхода для решения задачи кустования и размещения кустовых площадок.
Разработана процедура разбиения залежи на зоны, облегчающая применение
предлагаемых моделей рационального размещения скважин для крупных месторождений.
Основное отличие предлагаемого подхода по сравнению с существующими методиками
автоматизированного размещения скважин заключается в том, что расчеты по
геолого-математическим и гидродинамическим моделям проводятся один раз на
стадии получения исходных параметров моделей оптимизации.
Литература
1.
Гермейер Ю.Б. Введение в
теорию исследования операций. М.: Наука, 1971. - 384 c.
2.
Оразбаев Б.Б.,
Кусмолдина Ж.О., Мухамбетжанов А.Т. Формализация и математическая постановка
задачи оптимизации размещения скважин на нефтяной залежи и методы их решения//
Научный журнал «Вестник АИНГ», -Атырау:
-№20, 2010. -С.92-100.
3.
Ермолаев А.И., Ибрагимов
И.И. Модели рационального размещения скважин при разработке газовых и
газоконденсатных месторождений // Труды ИПУ им. В.А. Трапезникова РАН. Том
XXVII, 2006. – С.118-123.
4.
Абдикадыров Б.А. Модели
рационального размещения скважин на газовых залежах сложного геологического
строения//Дисс. канд. тех. наук.
–Москва: 2009. -129 с.
5.
Мину М. Математическое
программирование. Теория и алгоритмы. - М.: Наука, 1990 – 486 с.
6.
Сергиенко И.В., Шило
В.П. Задачи дискретной оптимизации. Проблемы, методы решения, исследования. –
Киев.: Наукова думка, 2003. - 242 с.
7.
Gomory R. E., An algorithm for
the mixed integer problem. Rand. Corp., P-1885, Santa Monica, California,
February 22, 1960. - Р.1885.
8.
Guéret C., Prins C., Sevaux M. Applications of optimization with
Xpress-MP // Editions Eyrolles, Paris, France, 2002. - Р.265.
9.
Лебедев С.С.
Целочисленное программирование и множители Лагранжа // Экономика и
математические методы. – 1984, -№3, -С.592-610.
10. Курейчик В.В., Балюк Л.В. Вероятностный генетический алгоритм Ant Colony и его приложение
для решения задач поиска (на примере задачи о коммивояжере) // Труды МНТК
«Интеллектуальные системы (IEEE AIS’04)» и «Интеллектуальные САПР (CAD-2004)».
- М.: Физматлит, 2004, -№1, -С.53-65.
11.
Holland J.H.
Adaptation in natural and artificial systems. An introductory analysis with application to biology, control,
and artificial intelligence. – London: Bradford book edition, 1994. -211 p.
12. Комбинаторные методы и алгоритмы решения задач
дискретной оптимизации большой размерности./ В.Р. Хачатуров, В.Е.Веселовский,
А.В. Злотов и др. -М.: Наука, 2000. –360 с.