Математика/4. Прикладная математика

Каминский Д.Д., доцент к.ф-м.н. Букенов М.М.

Карагандинский государственный университет им. академика Е.А. Букетова

АССИМПТОТИЧЕКИЕ ОЦЕНКИ ДЛЯ ЗАДАЧИ О КРУЧЕНИИ БРУСА

Рассмотрим задачу о кручении изотропного цилиндрического бруса:

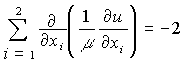, где

(1)

- константа Ламе. В качестве области выберем круг единичного радиуса с центром в начале координат. Тогда:

, .

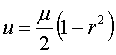Сформулируем вспомогательную задачу метода фиктивных областей для (1):

,

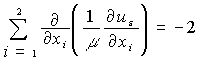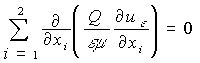, (2)

, , ,

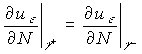где , значения и означают стремление нормали к границе изнутри и извне - производная по конормали.

В качестве области в задаче (2) выберем круг радиуса два с центром в начале координат. Полагая , получим следующее решение (2):

,

,

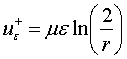В случае :

,

,

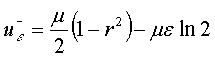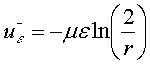Введем в рассмотренные степенные функциональные ряды:

,

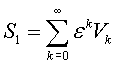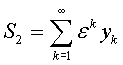, (3)

Определенные в областях и членами которых являются решения системы задач:

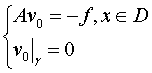
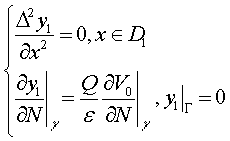(4)

для :

,

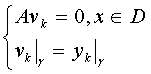
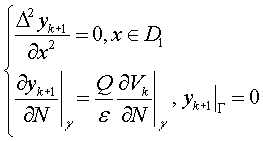где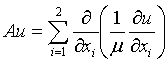

Функции , определены в области , а функции , определены во вспомогательной области . Данная система является системой задач трансмиссии. Нахождение неизвестных , осуществляется в следующем порядке: сначала определяется в , затем, с учетом условий согласования и , на , находится решение в области . По найденному можно определить решение в области и т.д. Заметим, что при сделанных предположениях все задачи из системы (4) разрешены и их решения единственны в , так что .

Выясним условия, при которых ряды и определенные равенством (3), сходятся к решению задачи (2).

Теорема 1. Существует такое, что для всех , ряды , (3) абсолютно сходятся в , соответственно и имеют место равенства:

; (5)

где - решение (2).

Доказательство: для доказательства абсолютной сходимости рядов воспользуемся оценками неоднородных граничных задач. Используя однородные оценки решений и следов функций, а так же условия согласования на находим, что:

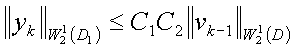(6)

Оценка (6) показывает сходимость ряда в при условии сходимости в норме пространства . Для доказательства сходимости ряда поступаем аналогично:

,

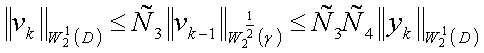
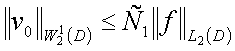(6`)

В силу признака Даламбера при получаем абсолютную сходимость ряда в , а из (6) и ряда в . Из полноты пространства следует, что . Умножая уравнения относительно , из системы (4) на и суммируя по всем , приходим к задаче:

 ,

, , ,

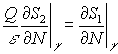совпадающей, как нетрудно проверить с (2). Тем самым имеют место равенства (5). Для доказательства теоремы 1 осталось проверить законность операций:

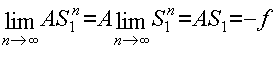
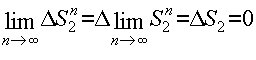(7)

которыми мы воспользовались при формальном суммировании членов , . Здесь через и обозначены частичные суммы рядов , . Из теории операторов следует ограниченность операторов А, , действующих из в и из в соответственно. В силу ограниченности А, и перечисленных свойств следует равенство , и законность операций (7) для всех . Теорема 1 доказана.

Замечание 1. Из теоремы следует оценка близости:

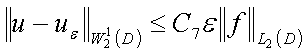(8)

Для этого достаточно сравнить - решение (1) с в области . В силу построения совпадает с первым членом разложения по степеням малого параметра , поэтому:

При условии ряд 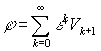абсолютно сходится в и вместе с оценкой (6’) влечет за собой (8). Ясно, что при полученная оценка неулучшаемая по .

Замечание 2. Из теоремы следует однозначная разрешимость вспомогательной задачи (2) для всех .

Множитель , введенный при коэффициенте играет специальную роль. Смысл заключается в том, чтобы наряду с - решением (2), рассмотреть другое решение - той же задачи (2), но с . На основании теоремы 1 имеют место следующие разложения:

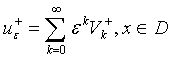
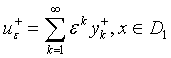(9)

Здесь , обозначены решения из системы (4), в которой параметр принимает значение, равное единице. По той же причине, для справедливы разложения:

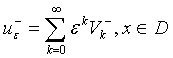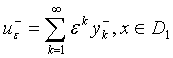, (10)

В которых через , обозначены решения (4) с . Покажем, что и связаны между собой соотношениями:

=, – четное; = -, - нечетное (11)

Для этого рассмотрим , которое является решением задачи:

,

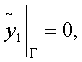
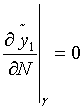
Ясно, что , поэтому . Далее, обозначим . Тогда решение задачи:

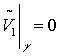, (12)

Из (12) следует и равенство . Продолжая подобные рассуждения, приходим к (11).

При =0, очевидно, , где - решение (1). С учетом (11) перепишем разложения (9), (10) в области в следующем виде:

(13)

Используя полученное представление (13) и оценку (6) находим, что при всех :

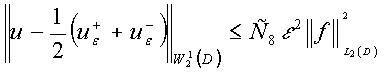
Полученный результат сформулируем в виде теоремы.

Теорема 2. Для всех справедлива оценка:

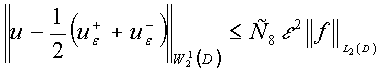(14)

где - решение (1), , - решение (2), соответствующие выбору и .

Тогда для всех и имеет место асимптотическое поточечное двустороннее неравенство:

(15)

Доказательство этих утверждений непосредственно следует из предыдущих рассуждений. Точность получаемых двусторонних приближений ограничена оценкой (15).

Для того чтобы получить двусторонние оценки решения () с заданной точностью применим идею экстраполяции Ричардсона. Построим экстраполированные решения , являющиеся линейной комбинацией, с некоторыми весами:

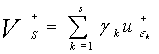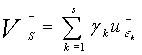, ; (16)

Корректный вид коэффициентов зависит от выбора последовательности и показателя точности .

Наиболее распространенным является выбор:

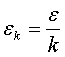, (17)

При котором коэффициенты находятся в явной форме:

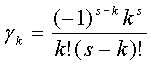, (18)

и удовлетворяют условиям: , ,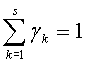

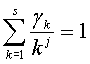При таком способе задания , находим что:

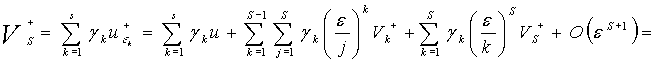
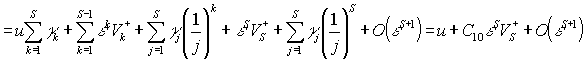, где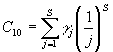

Совершенно аналогично . Пусть - нечетное, тогда , значит:

(19)

С помощью этого представления доказывается теорема 3.

Теорема 3. Пусть , – решение (1), , - решения (2), соответствующие выбору , .

Тогда для всех и имеет место ассимптотическое поточное двустороннее неравенство:

(20)

и оценки близости:

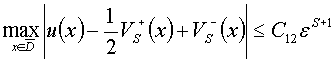(21)

где – нечетное, определяется по формулам (16).

Литература:

1. Коновалов А.Н., Метод фиктивных областей в задачах кручения – «Численные методы механики сплошной среды», 1973, Новосибирск, т. 4, №2, стр. 109-116;

2. Букенов М.М., Малые параметры в алгоритмах задач теории упругости, 1986, Новосибирск, стр. 124.