Математика/4.Прикладная математика
Рябоштан
А.Ф., к.т.н. Миленин А.Н.
Харьковский
национальный технический университет
сельского
хозяйства им. П. Василенко
Построение пространственных решеток в расчетах межлопаточного
пространства газовых турбин
При
аэродинамических расчетах газовых турбин область, находящуюся между
двумя соседними лопатками, приходится рассматривать как составленную из
некоторого количества вложенных в нее областей. Для этого передняя и задняя
поверхности лопатки в настоящее время аппроксимируются некоторой совокупностью плоских
четырехугольников, общее количество которых определяется требуемой точностью
аппроксимации.
Задание этих четырехугольников
координатами их вершин, а также построение пространственной решетки между двумя
соседними лопатками требует значительного объема памяти ЭВМ и из-за его
нехватки бывает затруднительно.
Если поверхности, образующие решетку
внутри рассматриваемого объема, задавать аналитически, то это позволит
значительно сократить необходимый объем памяти ЭВМ.
Для решения этой задачи нами предложена
трехпараметрическая формула /I/, задающая некоторый объем (рис. I), которая после ряда преобразований может быть
записана в виде:
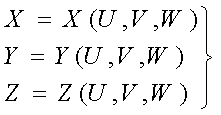 (1)
(1)
где:
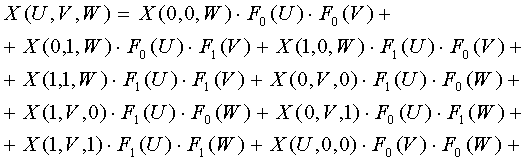 (2)
(2)
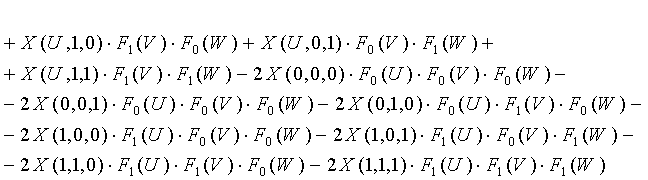
Здесь:
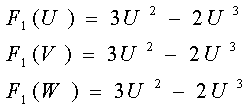
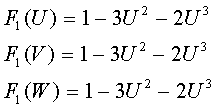 (3)
(3)
![]()
![]() - граничная кривая
рассматриваемого объекта у точек которой
- граничная кривая
рассматриваемого объекта у точек которой ![]()
![]()
![]()
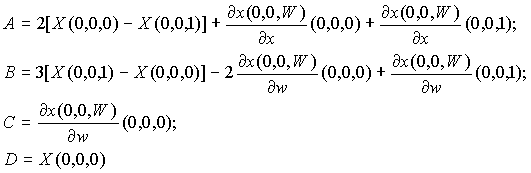 (4)
(4)
В выражении (4) ![]() – значения координаты
Х в конечных точках рассматриваемой кривой
– значения координаты
Х в конечных точках рассматриваемой кривой ![]() и
и ![]() - значения
производных по параметру W в этих точках. Аналогично определяются остальные
криволинейные стороны рассматриваемого объема.
- значения
производных по параметру W в этих точках. Аналогично определяются остальные
криволинейные стороны рассматриваемого объема.
Производные могут быть определены одним из
методов численного дифференцирования.
В нашем случае граничные кривые верхнего и
нижнего оснований криволинейного шестигранника являются плоскими кривыми ![]() .
.
В этом случае имеют вид:
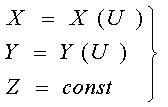 или
или 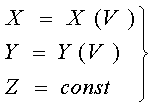 (5)
(5)
Величина Z определяется как высота соответствующего сечения
лопатки. Кривые сечений лопатки имеют вид:.![]() .
.
Если параметр U выразить
через координаты концов в виде 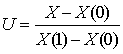 ,то параметрическое
уравнение координаты Х примет вид:
,то параметрическое
уравнение координаты Х примет вид:
![]() (6)
(6)
Тогда параметрическое уравнение координаты Y имеет вид:
![]() (7)
(7)
Дифференцированием (6) и (7) по параметру определяются частные производные в
вершинах шестигранника.
Боковые ребра шестигранника – прямые линии. Их
параметрические уравнения
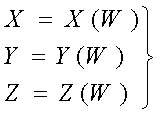 (8)
(8)
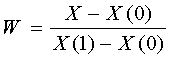 ;
;
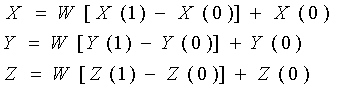 (9)
(9)
Формула (2) может быть записана в виде более удобном
для практического применения (через координаты вершин рассматриваемого
криволинейного шестигранника и производные по параметрам в этих вершинах
(рис.1)):
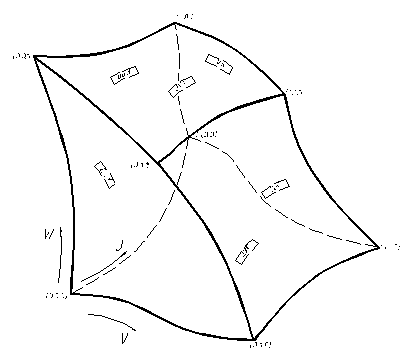
Рис. 1
Необходимым условием получения ортогональной
пространственной решетки является наличие в ее основании ортогональной сетки
двух семейств кривых. Построение такой сетки приведено в работе /2/.
ЛИТЕРАТУРА
1.
Сластин Ю.В., Рябоштан А.Ф. Трехпараметрическая формула задания поверхностей
сложных технических форм.- В кН.»Применение новейших математических методов и
вычислительной техники в решении инженерных задач». Сб.научн.тр.МИИСП, М.,1980.
2.
Найдыш В.М., Сластин Ю.В., Рябоштан А.Ф. Некоторые вопросы построения
ортогональных сеток полиномов. - В кн. «Прикладная
геометрия и инженерная графика».Киев.Будивельник,1984,вып.38,с.99-100.