К.ф.-м.н. Р. І. Собкович, к.ф.-м.н. А.І. Казмерчук

Прикарпатський національний університет імені В.Стефаника

Дослідження n-точкових крайових задач з параметром

Розглянемо систему диференціальних рівнянь

, (1)

де та параметр - вектори - вимірного евклідового простору , - не вироджена матриця, та поставимо задачу відшукання її розв’язків, які задовольняють умовам

, , … (2)

Оскільки кількість умов, яким повинен задовольняти розв’язок, більша від порядку системи, то задача (1), (2), взагалі кажучи, розв’язків може не мати. Досягти виконання всіх умов (2) можна за рахунок вдалого вибору параметра , який у цьому випадку виступає у ролі керування. Подібні задачі для скалярного рівняння, а також у лінійному випадку розглядалися у ряді робіт (див.,наприклад,[1]). Задача для нелінійной системи диференціальних рівнянь розглядається вперше.

Нехай функція визначена та неперервна в області , ,

Означення. Пару будемо називати розв’язком задачі (1), (2), якщо функція разів диференційовна на відрізку , , , тотожно задовольняється рівність

,

а також виконуються умови .

Із неперервності функції випливає існування таких векторних констант та , що для всіх точок області покоординатно виконується нерівність

(3)

Нехай - множина векторів , координати яких задовольняють умовам

+, ,

,

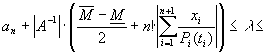
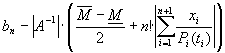де ,

,

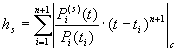
Теорема 1. Нехай функція визначена та неперервна в області , виконується нерівність (3), а також множина не порожня. Тоді задача (1), (2) має в хоча б один розв’язок.

При доведенні використовується оператор :

,

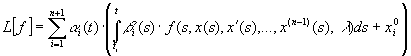який довільну неперервну на проміжку функцію відображає у разів диференційовну на цьому проміжку функцію , яка задовольняє умовам ,

Теорема 2. Нехай виконуються умови теореми 1, нерівність (3), а також всі власні значення матриці ,що визначається даними задачі, лежать в одиничному крузі. Тоді задача (1), (2) має єдиний розв’язок , до якого при рівномірно по збігається послідовність векторних функцій в ітерційному процесі з використанням оператора

.

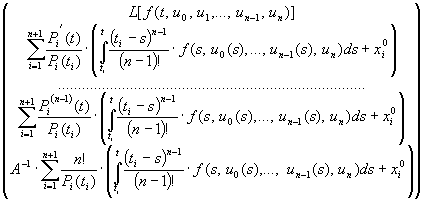При цьому похибка характеризується нерівністю

,

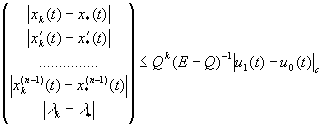де - одинична матриця,

Література

1. G. Zwirner. Про одну крайову задачу для диференціального рівняння . Atti Ist. veneto sci. lett. ed arti. Gl. sci mat. e natur, 1973-1974, 132, s. 531-554.