Технические науки/ 4. Транспорт

К.т.н Жуманов М.А.

Казахский национальный технический университет имени К.И.Сатпаева

НЕКОТОРЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ОТКАЗОВ ТРАНСПОРТНОЙ ТЕХНИКИ

Важным в теории вероятностей является понятие случайной величины, т.е. величины, которая в результате опыта можеть принять то или иное неивестное заранее значение /1/.

Процесс возникновения отказов транспортной техники носит многопричинный, случайный характер, поэтому оценки числовых показателей надежности машин проводятся методами теории вероятностей и математической статистики.

Статистическая информация об отказах получается из наблюдений за эксплуатацией или испытаниями в заданных условиях одинаковых объектов. Каждый объект работает от начала его эксплуатации до первого отказа и после отказа не восстанавливается и не заменяется работоспособным. Испытания считаются законченными после отказа всех объектов. При этом определяются наработки каждого объекта от начала его эксплуатации до первого отказа и записываются в виде вариационного ряда.

Закон распределения случайной величины является ее универсальной вероятностной характеристикой. Законом распределения вероятностей случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями /2/. Закон распределения имеет разные формы: ряд распределения, интегральная функция распределения и дифференциальная функция распределения.

Нормальное распределение. При анализе, контроле и испытании изделий на надежность особое место занимает нормальное распределение, имеющее широкое распространение на практике /4/. Нормальным распределением называется распределение вероятностей непрерывной случайной величины, которая может принимать как отрицательные, так и положительные значения во всем диапазоне возможных значений от минус бесконечности до плюс бесконечности.

Кривая нормального распределения (рис. 1) имеет симметричный холмообразный вид. Вид ее описывает следующее математическое выражение:

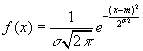
где σ — среднее квадратичное отклонение случайной величины;

е = 2,718 28 — основание натурального логарифма;

т — среднее значение нормального распределения.

Максимальная ордината кривой, равная соответствует точке х = т. По мере удаления от точки т плотность распределения падает при х →±∞ кривая асимптотически приближается к оси абсцисс. Эта кривая известна под названиями: кривая Гаусса, кривая Лапласа, кривая ошибок, вероятностная кривая и т. п.

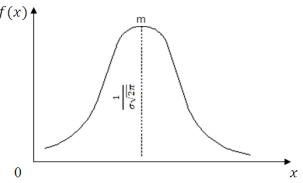
Рис. 1. Кривая нормального распределения

Нормальное распределение возникает тогда, когда на исследуемую величину действует множество случайных факторов, каждый из которых вносит незначительный вклад в суммарное значение отклонения величины от ее среднего значения, но ни один из них не является превалирующим над всеми другими, так как в противном случае закон распределения этой превалирующей ошибки будет влиять на сумму и определит ее закон распределения.

Некоторые исследователи полагают, что процесс изнашивания подобен процессу механической обработки, при котором размеры деталей, как правило, распределяются по нормальному закону. Поэтому и размеры изношенных деталей распределяются поэтому же закону.

Суммарная наработка восстанавливаемого изделия до капитального ремонта в ряде случаев приближенно распределена по нормальному закону. По этому же закону иногда распределено время восстановления ремонтируемых изделий. Кроме того, нормальное распределение часто используется для приближенных расчетов в тех случаях, когда имеет место биноминальное распределение или распределение Пуассона.

Экспоненциальный закон распределения отказов используется для
прогнозирования вероятности безотказной работы изделий во времени.

Вероятность безотказной работы изделия определяется по формуле

где — интенсивность отказов;

t — время работы, для которого определяется P(t).

На рис. 2 представлены характеристики экспоненциального распределения наработки до отказа.

Рис.2 Характеристики экспоненциального распределения

Характерной особенностью экспоненциального закона является то, что вероятность отказа изделия в некоторый период времени не зависит от наработки к началу этого периода. Интенсивность отказов является величиной постоянной, равной параметру распределения.

В транспортной технике работоспособность конструктивно доведенного изделия делится на три периода: I — приработка и выявление дефектов: II — нормальная эксплуатация; III — старение (рис.3).

Рис.3 Интенсивность потока отказов техники

Для каждого из указанных периодов, имеющих свои особенности, отказы характеризуются различными статистическими распределениями, требующими различной математической обработки. Экспоненциальный закон применяется для периода нормальной эксплуатации конструктивно доведенного изделия.

В машиностроении экспоненциальному закону подчиняются отказы изделий, имеющих характер внезапных поломок, обусловленных случайными перегрузками, несвойственными обычной эксплуатации, а также отказы, вызываемые засорением, различными механическими повреждениями, ослаблением крепления /4/.

Закон Вейбулла. Вероятность безотказной работы изделия определяется по формуле

Интенсивность отказов

Средняя наработка до отказа

Применение распределения Вейбулла весьма разнообразно. По своим свойствам оно занимает промежуточное положение между нормальным и экспоненциальными распределениями. Эта особенность распределения позволяет использовать его для описания безотказности обьектов в течение трех периодов их эксплуатации: приработки, нормальной эксплуатации и старения.

Список литературы

1.Топчиев.А.В., Гетопанов В.Н., Солод В.И., Шпильберг. Надежность горных машин и комплексов. Изд-во «Недра», 1968.

2. Брауде В.Н., Семенов Л.Н. Надежность подъемно-транспортных машин. Л.:Машиностроение, 1986. 183 с.

3. Елизаветин М.А. Повышение надежности машин. М., «Машиностроение», 1968, 267 с.

4. Котляревский Г.П. Основы повышения надежности и долговечности горношахтного оборудования. Изд-во «Недра», 1971.200 с.