Карачун В.В., Мельник В.Н.
Национальный технический университет Украины «КПИ»
НЕПОЛНЫЙ ПРОСТРАНСТВЕННО-ЧАСТОТНЫЙ РЕЗОНАНС В ПЛОСКОЙ
ПРЕГРАДЕ
В отличие от
известного, рассмотрим случай, когда 
, 
.
Это означает, что при этих условиях точно совпадают узловые линии 
-ой
и 
-ой
форм падающей звуковой волны давления и изгибной волны, но только в направлении
оси х (если 
,
а 
,
то совпадение линий узлов будет в направлении оси y).
Максимальное значение
работы 
падающей звуковой волны давления 
на перемещении 
в этом случае будет таким
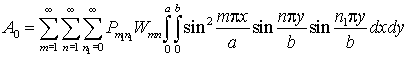. (1)
Проведя операцию
интегрирования, получим –
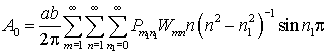. (2)
Подставляя
соотношения (1) и (2) в уравнение пластины определим значения прогибов пластины
для трех значений индексов – m, n и n1:
. (3)
Очевидно, что при 
и т.д. величины прогибов максимальны.
Если падающая волна
давления имеет вид двойного тригонометрического ряда, то после подстановки в
уравнение движения можем определить прогиб пластины при непрерывном воздействии
звукового давления, включая вынужденные и собственные колебания:
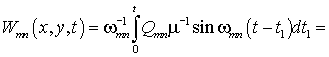
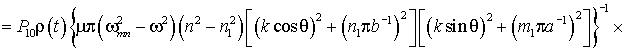
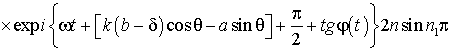. (4)
Закон изгибных
колебаний будет определяться выражением
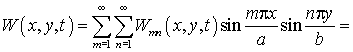
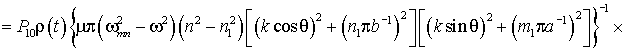
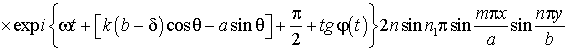. (5)
Анализ показывает,
что при одновременном равенстве 
и 
имеет место пространственно-частотный
резонанс, приводящий к неограниченному возрастанию амплитуды изгибных
колебаний. Если выполняется лишь одно из равенств, то проявляется один из
резонансов – пространственный (
)
или частотный (
).
Очевидно, что при 
и далее для последующих нечетных значений 
и т.д., величина прогиба пластины
максимальна. При 
изгиб пластины равен нулю. Эти уравнения
определяют линии узлов.
Вычисления
показывают, что распределение акустической вибрации в пространстве имеет тот же
характер, что и при пространственно-частотном резонансе, однако абсолютные
значения прогибов пластины при прочих равных условиях существенно меньше (табл.
1, табл.2).
Таблица 1 Значения максимальных прогибов пластины конечных размеров при неполном
пространственно-частотном резонансе
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
0,218 |
2 |
1 |
2 |
0,187 |
3 |
1 |
2 |
0,077 |
|
3 |
0,127 |
3 |
0,107 |
3 |
0,040 |
||||||
|
4 |
0,088 |
4 |
0,071 |
4 |
0,029 |
||||||
|
5 |
0,088 |
5 |
0,059 |
5 |
0,024 |
||||||
|
2 |
1 |
0,196 |
2 |
1 |
0,156 |
2 |
1 |
0,056 |
|||
|
3 |
0,350 |
3 |
0,267 |
3 |
0,079 |
||||||
|
4 |
0,187 |
4 |
0,148 |
4 |
0,059 |
||||||
|
5 |
0,140 |
5 |
0,111 |
5 |
0,047 |
||||||
|
3 |
1 |
0,029 |
3 |
1 |
0,023 |
3 |
1 |
0,005 |
|||
|
2 |
0,092 |
2 |
0,075 |
2 |
0,029 |
||||||
|
4 |
0,125 |
4 |
0,101 |
4 |
0,042 |
||||||
|
5 |
0,072 |
5 |
0,059 |
5 |
0,024 |
||||||
|
4 |
1 |
0,039 |
4 |
1 |
0,031 |
4 |
1 |
0,112 |
|||
|
2 |
0,098 |
2 |
0,074 |
2 |
0,025 |
||||||
|
3 |
0,249 |
3 |
0,198 |
3 |
0,049 |
||||||
|
5 |
0,328 |
5 |
0,260 |
5 |
0,108 |
||||||
|
5 |
1 |
0,011 |
5 |
1 |
0,009 |
5 |
1 |
0,003 |
|||
|
2 |
0,026 |
2 |
0,021 |
2 |
0,005 |
||||||
|
3 |
0,051 |
3 |
0,038 |
3 |
0,016 |
||||||
|
4 |
0,116 |
4 |
0,095 |
4 |
0,039 |
, м
, м
, м
Таблица 2 Значения максимальных прогибов пластины конечных размеров при неполном
пространственно-частотном резонансе
|
|
|
|
|
|
|
|
|
|
4 |
1 |
2 |
0,094 |
5 |
1 |
2 |
0,047 |
|
3 |
0,052 |
3 |
0,025 |
||||
|
4 |
0,036 |
4 |
0,018 |
||||
|
5 |
0,029 |
5 |
0,015 |
||||
|
2 |
1 |
0,035 |
2 |
1 |
0,032 |
||
|
3 |
0,139 |
3 |
0,050 |
||||
|
4 |
0,074 |
4 |
0,038 |
||||
|
5 |
0,056 |
5 |
0,028 |
||||
|
3 |
1 |
0,008 |
3 |
1 |
0,005 |
||
|
2 |
0,037 |
2 |
0,019 |
||||
|
4 |
0,051 |
4 |
0,025 |
||||
|
5 |
0,029 |
5 |
0,016 |
||||
|
4 |
1 |
0,009 |
4 |
1 |
0,005 |
||
|
2 |
0,037 |
2 |
0,002 |
||||
|
3 |
0,081 |
3 |
0,050 |
||||
|
5 |
0,130 |
5 |
0,050 |
||||
|
5 |
1 |
0,004 |
5 |
1 |
0,002 |
||
|
2 |
0,010 |
2 |
0,004 |
||||
|
3 |
0,021 |
3 |
0,010 |
||||
|
4 |
0,047 |
4 |
0,023 |
, м
, м
