ИССЛЕДОВАНИЯ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ ШАРОВОЙ ЗАГРУЗКИ В ПЛАНЕТАРНОЙ МЕЛЬНИЦЕ

 

Сексенбаева Р.Б., кандидат технических наук, доцент Казахского агротехнического университета, Казахстан, г.Астана.

Сулейменов Т.Б., доктор технических наук, профессор Евразийского университета, Казахстан, г.Астана.

 

Проблема разрушения различных материалов, в том числе и горных пород, при динамическом нагружении привлекает возрастающее внимание исследователей и инженеров. Это связано с практическим применением ударных и других импульсных методов создания интенсивных нагрузок в разнообразных технологических процессах дробления и измельчения горных пород. Разрушение определяют как появление новых или рост старых свободных поверхностей, которые в конечном счете вызывают разделение первоначального твердого тела на части. Экспериментальными исследованиями установлено, что разрушение представляет собой сложное физическое явление и включает в себя разрушение структурных элементов различного состава: микродефекты, макротрещины и т.п.

         Изучение реакции горных пород и минеральных сред на динамические нагрузки представляет сложную задачу, обусловленную специфическими особенностями их поведения при таких воздействиях. Времена ударных воздействий на твердые материалы таковы, что в них образуются конечные области возмущений с отличающимся друг от друга напряженно-деформированным состоянием. Другими словами, динамическое нагружение горных пород механическим способом вызывает изменения напряженно-деформированного состояния, роль которого определяется физико‑механическими характеристиками породы и режимом нагружения. Высокая интенсивность возникающих напряжений в горной породе приводит к качественно новым явлениям по сравнению со статической нагрузкой.

         Процессы дробления  и измельчения естественных минеральных сред и искусственных материалов являются определяющими во многих технологических процессах и схемах рудоподготовки. В их основе заложены различные способы разрушения материалов [1], наиболее распространенными из которых являются: удар, раздавливание и истирание. Выбор способа разрушения зависит от физико-механических свойств измельчаемого материала, начальной величины разрушаемых кусков, требуемой степени измельчения и ряда других факторов.

         В настоящее время совершенствование дробильно-измельчающих машин в Казахстане ведется в первую очередь в направлении снижения энергоемкости процесса измельчения. Это может быть достигнуто использованием таких механизмов разрушения, при которых в измельчаемом материале формируется сложное напряженное состояние с упругими деформациями сжатия, растяжения, изгиба и сдвига.

         В работе [2] на основе принципов, которые применялись при моделировании движения мелющей среды в обычных мельницах (каждое мелющее тело в процессе движения испытывает последовательность соударений с футеровкой мельницы или с другими мелющими телами; в промежутках между соударениями мелющие тела движутся под действием силы тяжести по параболическим траекториям; соударения представляются как мгновенные изменения скоростей) рассматривается алгоритм расчета движения мелющих тел в многотрубной мельнице.

         Представленная модель обеспечивает высокую точность определения различных конструктивно-технологических параметров многотрубных мельниц: потребляемую мощность, пусковой момент, динамические нагрузки, которые действуют на корпуса мельницы от загрузки, энергетические параметры взаимодействия мелющих тел и т.п. На основании представленного алгоритма расчета движения загрузки разработан пакет программ для персонального компьютера. Однако данная модель не учитывает элемент случайности в направлении движения шаров непосредственно перед соударениями, что несколько снижает точность получаемых результатов.

         Для описания движения загрузки в планетарной мельнице вводятся три системы координат: одна неподвижная и две подвижные.

         Центр неподвижной системы координат связан с центром мельницы (точка  на рис. 1 а). Эта система координат имеет постоянную ориентацию осей координат  и .

         Центр первой подвижной системы координат и связан с вращающимся водилом и проходит через центр помольной камеры (точка  на рис.1 а). Центр второй подвижной системы координат и связан с вращающейся камерой и также проходит через её центр. Центр первой подвижной системы координат совершает круговое движение по радиусу  с постоянной угловой скоростью  таким образом, что ось  все время направлена в начало неподвижной системы координат, а вторая подвижная система координат вращается относительно первой с угловой скоростью .

Положение шара характеризуется мгновенным положением центра помольной камеры  и угловым положением шара  по отношению к оси . Данная расчётная схема полностью описывает положение шара в помольной камере в любой момент времени, однако пользоваться ею для расчётов кинематических параметров загрузки неудобно из-за наличия нескольких подвижных систем координат. Приведём расчётную схему, показанную на рисунке 1а), к более удобному для расчётов виду, пользуясь свойством сложения вращений вокруг параллельных осей. Помольная камера участвует в двух вращениях: переносном с угловой скоростью  и относительном с угловой скоростью . На водиле  в рассматриваемый момент имеется точка , скорость которой равна нулю. По известной формуле механики имеем:

                                                                              (1)

Прямая, проходящая через точку , будет мгновенной осью вращений. Таким образом вместо двух вращений вокруг параллельных осей получено одно вращение вокруг оси . При этом:

                                                                                       (2)

Итоговая расчётная схема движения шара представлена на рисунке 1б). Рассматриваются две системы координат: одна неподвижная с осями  и , проходящими через центр вращений – точку  и вторая подвижная с осями и , центр которой связан с центром помольной камеры. При этом ось  все время направлена в начало неподвижной системы координат. Положение шара характеризуется мгновенным положением центра помольной камеры  и угловым положением шара  по отношению к оси .

Положение центра помольной камеры  характеризуется углом

,                                                                               (3)

где  - начальное угловое положение водила ;  - текущее время.

         Угловое положение шара  определяется численно в процессе решения задачи:

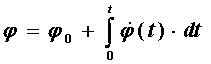                                                                                                                      (4)

В итоге, для абсолютной системы координат имеем:

,

,                      (5)

где - радиус помольной камеры.

За положительное направление угловых скоростей  и  выбрано направление на нас, соответствующее вращению против часовой стрелки на рис. 1б).

Переносная скорость шара:

                                                                               (6)

или                                                                                  (7)

Относительная скорость шара:

                                                                                                                                          (8)

или                                                                                             (9)

         Абсолютная скорость будет равна сумме относительной и переносной скоростей:

.                                                         (10)

         Ее величина рассчитывается по теореме косинусов:

,                                        (11)

где  - это угол между радиус-векторами  и :

.

         Абсолютное ускорение рассчитывается как сумма относительного, переносного и Кориолисова ускорений.

         Нормальное переносное ускорение:

                                                                                                              (12)

или                                                                                   (13)

Тангенциальное переносное ускорение  равняется нулю, т.к. водило и камера вращаются с постоянными угловыми скоростями:

При этом переносное угловое ускорение  равно нулю.

Нормальное относительное ускорение:

                                                                                  (14)

или                                                                                        (15)

Тангенциальное относительное ускорение:

                                                                                (16)

или ,                                                                                    (17)

где  - угловое относительное ускорение.

         Ускорение Кориолиса:

                                                                                                                                                   (18)

или                                                                                                         (19)

         Итоговое выражение для абсолютного ускорения шара принимает следующий вид:

 

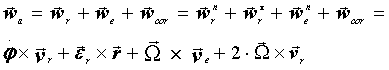                                                          (20)

Произведение  равно сумме внешних сил, приложенных к шару, т.е. – сумме силы реакции стенки помольной камеры  и силы трения .

.                     (21)

         Сила реакции стенки , естественно, направлена перпендикулярно поверхности стенки, т.е. – противоположно радиус-вектору . Сила трения  направлена перпендикулярно силе реакции стенки . Величина этой силы определяется обычным образом: . Эта сила сонаправлена разности скоростей поверхности стенки и шара (если скорость поверхности  больше скорости шара , то сила трения работает на увеличение относительной угловой скорости шара ).

Коэффициент трения  представляет собой функцию от пары материалов и разности скоростей шара и поверхности цилиндра

.                                                                                  (22)

         Этот коэффициент положителен при  и отрицателен в противном случае.

В итоге получаем:

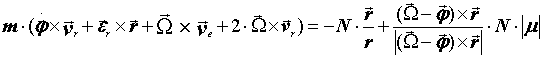     (23)

         Запишем проекции левой и правой частей этого уравнения.

         Вдоль радиус-вектора :

                                       (24)

         По нормали к радиус-вектору :

                                                   (25)

         Взяв отношение левых и правых частей, получаем:

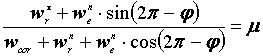                                                                                                    (26)

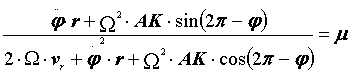или                                     (27)

         Выразим :

,

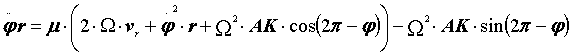или 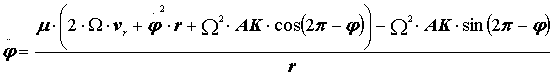(28)

 

Истирающее воздействие шара на материал отражает статическая составляющая импульса, а ударное разрушение характеризуется динамической составляющей. Данные параметры ударного импульса обуславливают достаточно большую площадь под кривой, описывающей его форму. Эта площадь, как было отмечено выше, пропорциональна энергии ударного импульса.

 

ЛИТЕРАТУРА

 

1.     Петров В.А., Андреев Е.Е., Биленко Л.Ф. Дробление, измельчение и грохочение полезных ископаемых. - М.: Недра, 1990. - 301 с.     

2.     Бендаж Д., Пирсон А. Прикладной анализ случайных данных. - М.: Мир, 1989г. 540с.

 

а)

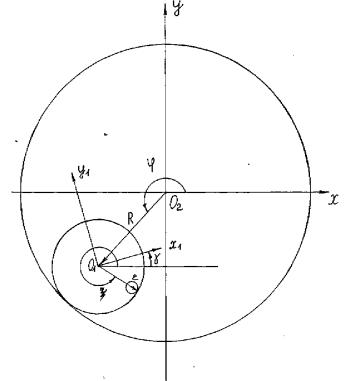
D:\Документы\Готовое\Отсканированные\Рисунки\22.bmp

б)

 

Рис3

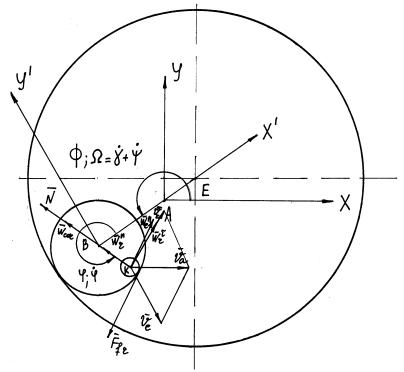
Рис. 1. Центр неподвижной системы координат