Технічні науки / 3. Галузеве машинобудування

Присяжний Л.В., Урбанюк Є.А., Баннов Г.М., Кузьма Л.М.

Хмельницький національний університет

МОДЕЛЮВАННЯ ПРОЦЕСУ НАВИВАННЯ ПРУЖИН З ВЕЛИКИМ ІНДЕКСОМ

Виготовлення пружин з великим індексом пов’язане зі значними зусиллями подачі прутка в зону формоутворення пружини. Традиційна методика визначення технологічних параметрів процесу навивання [1] ґрунтується на ряді допущень, які не дозволяють оцінити напружено-деформований стан прутка в зоні контакту його з формотворною оправкою. До таких допущень слід віднести наступні: а) точка контакту кінця прутка за [1] визначається наближено без врахування пружно-пластичних процесів; б) не враховується тертя прутка по поверхні інструменту. Наслідком наближених розрахунків є конструкція механізму навивання пружини, що має недоліки. При навиванні пружин великого індексу в таких пружиннонавивних автоматах спостерігається часте заклинювання прутка в механізмі навивання, що приводить до поломок і зупинки автомата та знижує його продуктивність.

Застосування сучасних методів розрахунку, зокрема чисельних з використанням комп’ютерних пакетів для моделювання процесів пружно-пластичної деформації дозволяє дослідити не лише усталений процес навивання, але й перехідні процеси в момент контакту кінця прутка з інструментом.

Метою дослідження є покращення параметрів технологічного процесу навивання пружин великого індексу шляхом використання чисельних методів і засобів комп’ютерного моделювання для отримання таких умов навивання, які виключають схоплювання кінця прутка з формотворною оправкою.

Для досягнення поставленої мети вирішено наступні завдання:

а) виконано аналіз існуючого методу навивання циліндричних пружин та методики розрахунку параметрів процесу;

б) розроблена методика деформування прутка при виготовленні пружин великого індексу з урахуванням тертя і контактної взаємодії;

в) проведено комп’ютерне моделювання процесу навивання пружин великого індексу та визначено параметри контактної взаємодії і зусилля подачі прутка для існуючої схеми навивання;

г) розроблена прогресивна схема навивання пружин з великим індексом, яка виключає заклинювання в інструментальному блоці.

Пружини великого індексу отримують на пружинонавивних автоматах. На рисунку 1 показано конструктивну (а) і кінематичну (б) схему такого автомата.

Пружина навивається в інструментальному блоці 1 (рис. 1) з оправкою 16, що обертається, і згинальними роликами 2 і 14. Кінці загинаються упором радіусу 12 на проводці. У навивальний інструмент пруток 22 подається кліщами 8, змонтованими на повзунці 5; повзунка приводиться від кривошипно-кулісного механізму 23 за допомогою сережки 24. Захоплення прутка здійснюється губками 6, встановленими в кліщах 8. Сила затиску прутка регулюється гвинтами 7. Важелі повертаються навколо своїх осей через ролики 11 за допомогою кулачка 10 і пружини 9. Кулачок 10 повертається при гойданні повідця 20, ролик 19 якого входить в паз важеля, що коливається, 18. Пруток прямує проводкою 17, встановленою в корпусі 4, зв'язаному качалками і пружинами з блоком .

Рухомий ніж 13 встановлений на кінці важеля 21 механізму відрізки від приводного валу 27, через приймальний 25 і передавальний 26 вали і при русі по замкнутій траєкторії входить всередину спіралі; опускаючись, він відрізує готову пружину. Відрізка пружини від спіралі здійснюється двома ножами. Нерухомий ніж 15 поміщений в утримувачі 3, закріпленому на блоці 1. Положення ножів щодо зовнішнього діаметру спіралі регулюється гвинтами.

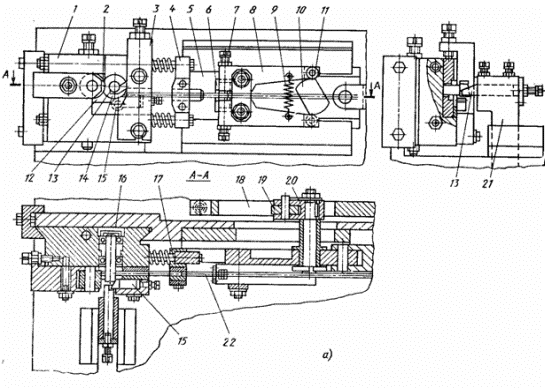
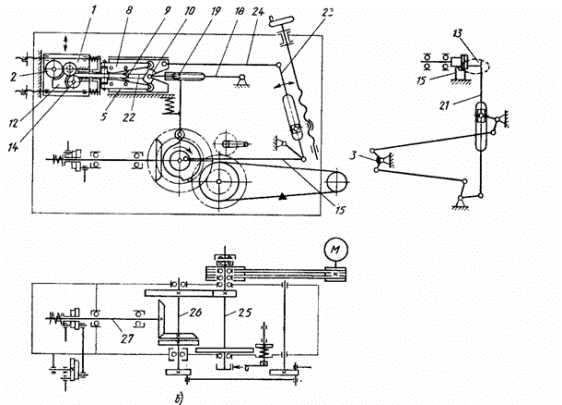
Рис.1. Конструктивна (а) і кінематична схема пружиннонавивного автомата

За допомогою графічного пакету SolidWorks була побудована комп’ютерна модель інструментального блока автомата (рис. 2).

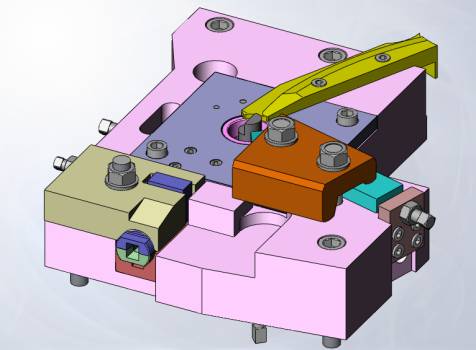
Рис.2 – 3D-модель інструментального блока пружиннонавивного автомата

Технологічний процес виготовлення пружини в інструментальному блоці складається з трьох стадій: а) подача прутка; б) навивання витків пружини; в) відрізання готової заготовки.

Навивання прутка відбувається за рахунок проштовхування прутка кліщами механізму подачі через інструментальний блок.

Кінець прутка подається в канал стаціонарної проводки 1 (рис.3), ковзає по гвинтовій (I) поверхні оправки і закручується в направляючому сегменті 2 (рис.3). Стаціонарна проводка має перегин в поздовжньому напрямку для утворення кута підйому пружини. Подальше навивання прутка в спіраль діаметра D відбувається за рахунок його контакту і дією сил тертя з обоймою, яка вільно обертається навколо своєї осі.

За існуючою методикою проводився розрахунок зусилля подачі прутка [1]: D=39 мм; a =8 мм; b = 10 мм.

а) площа поперечного перерізу прутка:

F = a × h =8 × 10 = 80 мм²,

де a і h – розміри профілю.

б) довжина розгортки заготовки:

L = 2.75π(d +h),

де d – внутрішній діаметр пружини.

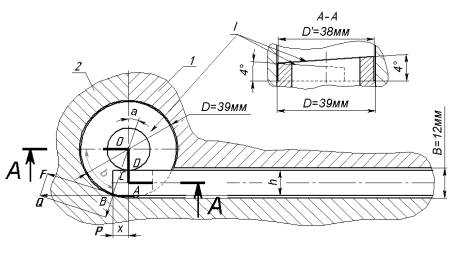а)

б)

Рис. 3 – Схема навивання пружини (а) та профіль дроту (б)

d = D – 2a = 39 - 2×8 = 23 мм,

де D – зовнішній діаметр пружини.

L = 2.75π(d +h ) =2.75×3.14×(23 +8) =267.7 мм.

в) кут силового трикутника:

β = arccos (P₀/Q₀) = 90⁰ – α,

де P₀ – нормальна складова.

З трикутників COD і AOD маємо:

sin α = x/ОВ = CD/OC,

звідси: CD = OC×x/OB = d×x/D,

де x – абсциса точки контакту кінця прутка (приймаємо x = 1.4a = 1.4×8 = 11.2 мм).

CD = 23×11.2/39 = 6.6 мм,

sin α = 11.2/0.5×39 = 0.5744;

α =35⁰, β = 90⁰ – α = 90⁰ – 35⁰.

г) початкове зусилля подачі:

Q₀ = M/OC = M/CD×cos β,

де M – згинальний момент;

д) момент пружно-пластичного згину:

М = Kσ_sW_x ,

де K – коефіцієнт профілю (приймаймо K =1.5);

σ_s – межа текучості (для сталі 65Г σ_s = 7.5×10⁸ Н/м²);

W_x – осьовий момент опору:

W_x = a×h²/6 =0.008×0.01²/6 = 1.3×10^-7 м³.

M = 1.5×7.5×10⁸×1.3×10^-7 = 150 Нм.

Q₀ = 150/0.0066×cos 55⁰ =39624 H.

е) зусилля подачі в процесі навивання;

При заправці прутка з попередньо обробленим кінцем (скіс під кутом 30°), зусилля подачі буде рівним зусиллю при усталеному процесі навивання, яке без урахування тертя в опорах і на інструменті буде наступним:

Q = P = M/OC = 2M/d =2×150/0.023 = 13043 H.

Для виконання досліджень процесу навивання пружини була побудована твердотільна модель системи «пруток-оправка» з відповідними параметрами (рис.4) в пакеті SolidWorks та проведено попереднє моделювання процесу пластичного деформування дроту в режимі виконання нелінійного аналізу та лінійного статичного аналізу в CosmosWorks (метод переміщень). Задача виявилась занадто складною, а розрахунок вимагав значних витрат часу (більше 10 год.). Результати моделювання виявились незакінченими, так як використані ітераційні методи не дали збігання розв’язку.

Надалі моделювання проводили в режимі лише лінійного статичного аналізу на двох спрощених моделях – пазовій та циліндричній, якими було замінено вихідну модель пружини.

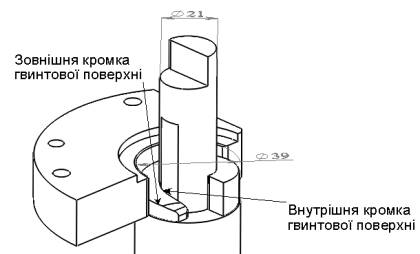
Рис. 4 – Параметри гвинтової поверхні оправки

Пазова модель (рис.5) представляє собою модель взаємодії прутка з гвинтовою поверхнею оправки (рис.4).

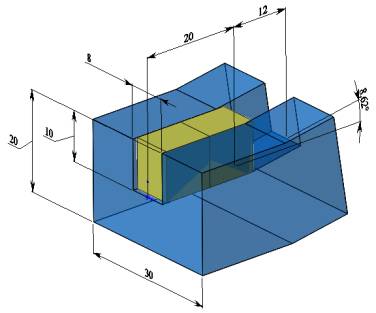
Рис.5 – Загальний вигляд пазової моделі

Оскільки найбільші контактні напруження виникають на початку взаємодії прутка з канавкою, то моделювання проводили при малих переміщеннях прутка (h=1–10 мм).

Для оцінки впливу тертя на параметри процесу, моделювання проводили при різних коефіцієнтах тертя.

Орієнтовні коефіцієнти тертя ковзання за [2]: а) сталь по сталі (без змащування) – 0,15; б) сталь по сталі (зі змащуванням) – 0,1-0,05.

Орієнтовні коефіцієнти тертя кочення [2]: а) сталь по сталі (м’якій) – 0,005; б) сталь по сталі (гартованій) – 0,001.

Для моделювання були вибрані наступні коефіцієнти тертя f: 0,15; 0,05 та 0,01.

Циліндрична модель (рис. 6) представляє собою модель взаємодії прутка з боковою поверхнею оправки. Для зменшення розмірності задачі модель виконана зрізаною.

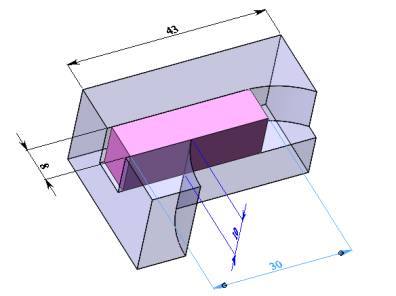
Рис. 7 – Загальний вигляд моделі з циліндричною поверхнею

Моделювання також проводили при малих переміщеннях прутка (h=1–10 мм), а для моделювання були вибрані такі ж коефіцієнти тертя: f=0,15; 0,05 та 0,01.

Для моделювання згину прутка в поздовжньому напрямку формотворного каналу інструментального блоку була використана пазова модель та проведено моделювання для переміщення h прутка на 5 та 10 мм і коефіцієнта тертя f=0,01.

Результати моделювання для h=10 мм і f=0,01 зображені на рис. 8–11.

Отримані значення параметрів зусилля подачі Q, сили тертя F_f, контактного тиску P_к та інтенсивності напружень s_i наведені у таблиці 1.

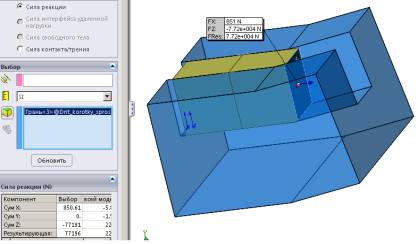
Рис. 8 – Визначення зусилля подачі Q прутка в пазовій моделі

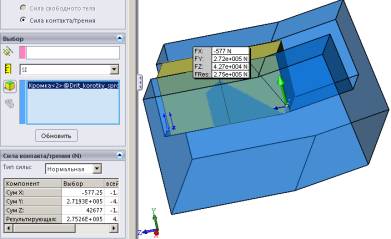
Рис.9 – Визначення сили тертя F_f прутка в пазовій моделі

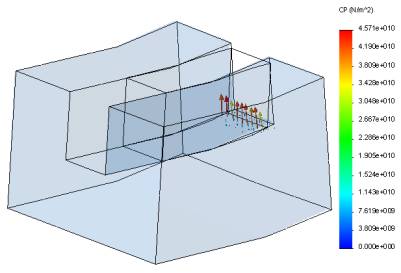
Рис. 10 – Розподіл контактного тиску P_к по поверхні прутка в пазовій моделі

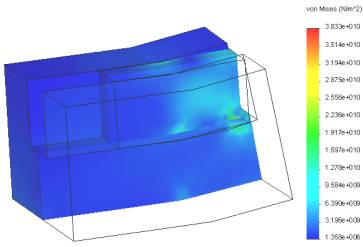
Рис. 11 – Розподіл інтенсивності напружень s_i в тілі прутка та оправки для пазової моделі

Таблиця 1 – Результати розрахунку параметрів процесу згину прутка для пазової моделі

№ досліду	Хід прутка h, мм	Параметри розрахунку
		Q´10^3, Н	Ff´10^3, Н	Pк´10^3, МПа	si´10^3, МПа
1	5,0	47,7	159	26	22,7
2	10,0	77,2	275	45	38

Для моделювання згину прутка в поперечному напрямку формотворного каналу інструментального блоку було використано циліндричну модель та проведено моделювання при малих переміщеннях прутка h (1; 2; 3; 4; 5 та 10 мм). Для моделювання були вибрані наступні коефіцієнти тертя f: 0,15, 0,05 та 0,01.

Результати моделювання для h=10 мм і f=0,15 зображені на рис. 12 – 15. Отримані значення параметрів зусилля подачі Q, сили тертя F_f, контактного тиску P_к та інтенсивності напружень s_i приведені у таблицях 2 – 5.

За отриманими результатами побудовані графіки залежності параметрів процесу згину прутка від величини подачі прутка.

Як видно з отриманих результатів процес деформування прутка в циліндричній моделі (рис.12 – 15) відбувається більш інтенсивно, ніж у пазовій (рис.8 – 11).

Проведений аналіз дає якісну картину впливу коефіцієнта тертя на процеси, які відбуваються в зоні контакту прутка з оправкою.

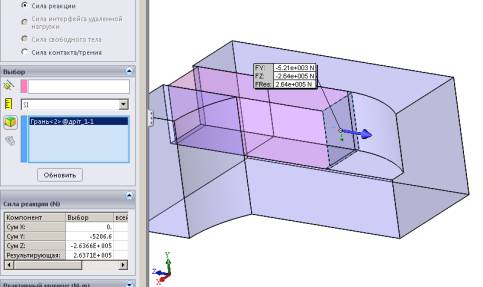
Рис. 12 – Визначення зусилля подачі Q прутка в циліндричній моделі

Таблиця 2 – Результати розрахунку зусилля подачі Q

№ досліду	Хід прутка h, мм	Зусилля подачі прутка Q, Н для коефіцієнтів тертя f
		0,15	0,05	0,01
1	1,0	29	22	16
2	2,0	581	817	290
3	3,0	4880	3270	1960
4	4,0	7860	5420	3100
5	5,0	17200	11500	5740
6	10,0	110000	62300	35600

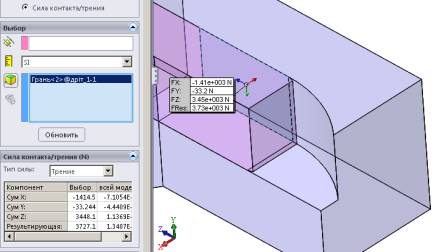
Рис. 13 – Визначення сили тертя F_f прутка в циліндричній моделі

Таблиця 3 – Результати розрахунку сили тертя F_f прутка по оправці

№ досліду	Хід прутка h, мм	Сила тертя Ff, Н для коефіцієнтів тертя f
		0,15	0,05	0,01
1	1,0	24,5	18,3	14,1
2	2,0	110	74,7	27,5
3	3,0	340	191	63
4	4,0	445	278	112
5	5,0	679	954	270
6	10,0	3730	1920	1040

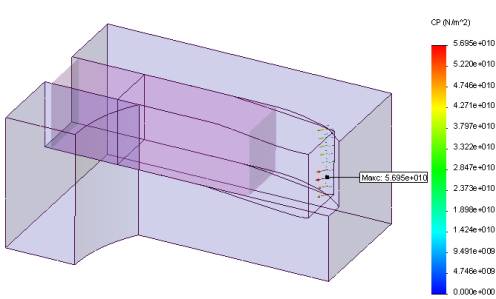
Рис. 14 – Розподіл контактного тиску P_к по поверхні прутка в циліндричній моделі

Таблиця 4 – Результати розрахунку контактного тиску Pк по поверхні прутка в циліндричній моделі

№ досліду	Хід прутка h, мм	Контактний тиск Pк, МПа для коефіцієнтів тертя f
		0,15	0,05	0,01
1	1,0	726	501	339
2	2,0	2971	1983	1045
3	3,0	8935	6041	3211
4	4,0	11680	8207	4812
5	5,0	17000	11426	6728
6	10,0	56950	37240	25500

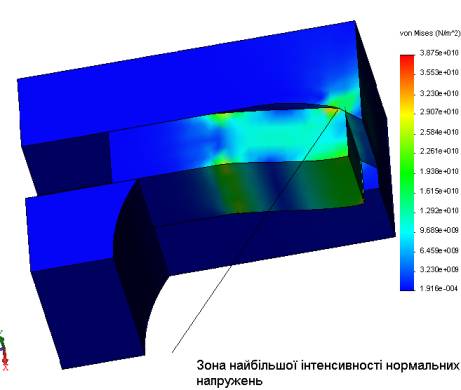
Рис. 15 – Розподіл інтенсивності напружень s_i в тілі прутка та оправки для циліндричної моделі

Таблиця 5 – Результати розрахунку інтенсивності напружень s_i

№ досліду	Хід прутка h, мм	Інтенсивність напружень за Мізисом si, МПа для коефіцієнтів тертя f
		0,15	0,05	0,01
1	1,0	595	478	362
2	2,0	2396	1987	1625
3	3,0	7288	5064	4450
4	4,0	9381	7503	6327
5	5,0	14040	9980	7902
6	10,0	38750	25140	20530

При контактному навантаженні зусилля діє на малій дільниці поверхні, внаслідок чого на поверхневому шарі металу виникають високі локальні напруження. В зоні дотику утворюється площадка, розміри якої залежать від пружності матеріалів та геометричних параметрів стискуваних поверхонь [3].

При цьому на поверхні оправки виникає наріст внаслідок схоплювання пошкоджених шарів матеріалів прутка і оправки.

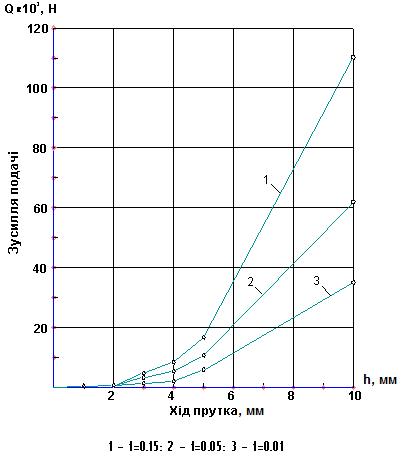
Рис.16 – Залежність зусилля подачі Q прутка від ходу h прутка і коефіцієнта тертя f

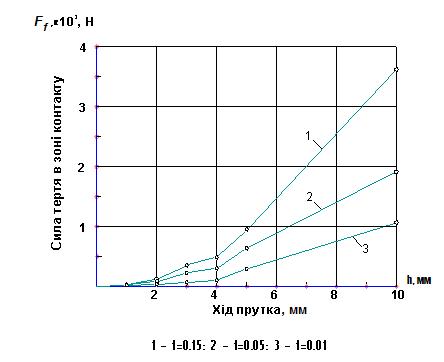
Рис.17 – Залежність сили тертя F_f прутка по оправці від ходу h прутка і коефіцієнта тертя f

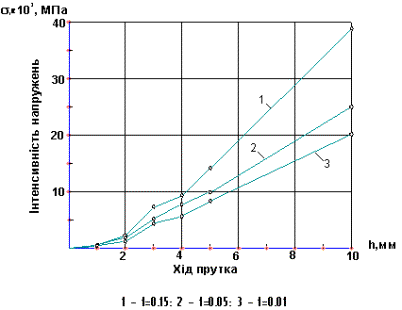
Рис.18 – Залежність інтенсивності напружень σ_i від ходу h прутка і коефіцієнта тертя f

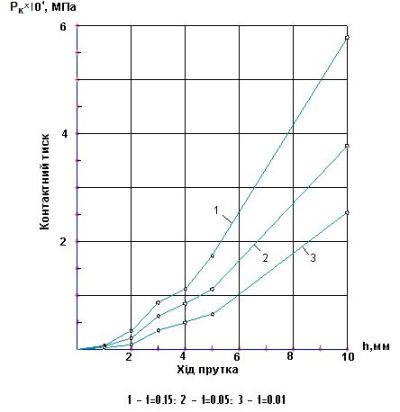
Рис.19 – Залежність контактного тиску P_к в зоні контакту прутка з оправкою від ходу h прутка і коефіцієнта тертя f

Для зменшення контактного тиску між прутком і оправкою в зону контакту існуючої конструкції (рис.20, а) були введені ролики (рис.20, б), які замінюють тертя ковзання на тертя кочення з проковзуванням.

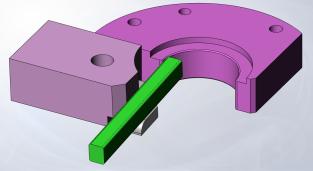
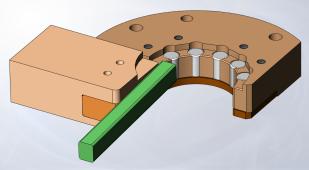
а) б)

Рис.20 – Комп’ютерні моделі існуючого (а) та запропонованого (б) вузла формоутворення пружини

Ммоделювання процесу навивання пружини у вдосконаленому вузлі дало наступні результати (для h=10 мм і f=0,001):

Q=17´10³ Н; F_f=411 Н; P_к=10,2´10³ МПа; s_i=16,5´10³ МПа.

Таким чином, результати підтверджують ефективність запропонованої конструкції, яка суттєво зменшує технологічне зусилля Q подачі прутка, силу тертя F_f, контактний тиск P_к та інтенсивність напружень s_i в зоні контакту.

Висновки

За результатами комп’ютерного моделювання процесу навивання пружини великого індексу та встановлення впливу коефіцієнта тертя на параметри процесу в зоні контакту прутка з оправкою, запропоновано конструктивне удосконалення формотворного вузла пружиннонавивного автомату. Проведені розрахунки вказують на те, що заміна тертя ковзання на кочення між прутком та оправкою шляхом введення елемента кочення – ролика, дозволяє позбутись негативних контактних явищ.

Література

1. Василишин С.А. Кузнечно-прессовое оборудование для изготовления изделий из проволоки. – Хмельницкий: ТУП, 2001. – 260 с.

2. Анурьев В.И. Справочник конструктора-машиностроителя. Т.1. – М.: Машиностроение, 2001. – 920 с.

3. Орлов П.И. Основы конструирования. Книга 1. – М.: Машиностроение, 1988. – 559 с.