Технические науки/2. Механика

Асп. Боровский Д.Н., к.т.н. Вайтехович П.Е.

Белорусский государственный технологический университет,

Республика Беларусь

Исследование движения элементов загрузки в центробежно-шаровой мельнице

Для изучения центробежно-шаровых мельниц необходимо иметь цельную математическую модель движения как материала, так и мелющих тел внутри этого агрегата. Она позволит спрогнозировать характер движения загрузки, который в свою очередь даст возможность определить геометрические размеры и технологические параметры мельницы.

Вертикальная центробежно-шаровая мельница включает цилиндрический корпус, внутри которого коаксиально установлен ротор. Над ротором с концентрическим зазором относительно него укреплено неподвижное кольцо. В такой конструкции движение мелющих тел (шаров) можно разделить на несколько стадий: относительное движение во вращающемся роторе, движение по статическому кольцу, соударение тел и их свободный полет с возвращением на плоское днище ротора.

Одним из важнейших конструктивных элементов центробежно-шаровой мельницы является вращающийся ротор, выполненный в виде диска сопряженного с цилиндроконической обечайкой. Высота ротора определяется высотой подъема измельчающих тел и материала. В предыдущих работах авторов [1, 2] с использованием позонного метода расчета была определена эта высота на основе анализа движения одиночного тела, при учете сил тяжести G, трения по поверхности F_Т, инерционной переносной F_е и кориолисовой F_с. В реальных условиях тела контактируют между собой, в результате чего возникают дополнительные силовые факторы, оказывающие влияние на характер движения. Перемещение шаров в роторе центробежно-шаровой мельницы в какой-то мере 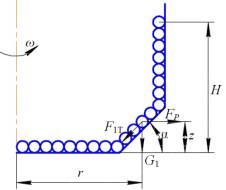упорядочено. Поэтому для учета взаимного влияния можно рассматривать движение в виде цепочки шаров, рисунок 1.

При такой модели движения на шар, находящийся в произвольной точке ротора, будут действовать дополнительные силы: F_р – сила давления (подпор) других шаров; G₁ – сила тяжести столбика шаров; F_1Т – сила трения между шарами, находящимися в соседних цепочках.

Для конического участка с учетом дополнительных силовых факторов уравнения относительного движения в подвижной цилиндрической системе координат примет вид

⁽¹⁾

По уравнению (1) были произведены расчеты максимальной высоты подъёма материала h_max частиц d_ч = 1 − 15 мм и шаров d_ш = 3 − 15 мм для ротора d_p = 0,1 − 0,75 м при изменении его угловой скорости ω = 30 – 150 рад/с. В расчетах принималось, что угол наклона образующей конического участка обечайки составлял 45°, а величина его катета 0,15r_р, где r_р – радиус ротора; коэффициент трения скольжения для материала f = 0,3, и трения качения для измельчающего тела – 0,0001.

В результате расчета установлено, что высота подъема как для материала, так и для мелющего тела при учете дополнительных усилий увеличивается. Это объясняется значительно большим влиянием силы давления, определяющее значение на которую оказывает инерционная переносная сила элементов загрузки.

Уменьшение размера как частицы материала (рис. 2), так и мелющего тела приводят к увеличению максимальной высоты подъема. Таким образом происходит распределение частиц по размерам непосредственно в роторе, что улучшает условия их измельчения и последующей сепарацией.

Адекватность математической модели подтверждена экспериментальна.

Отклонения расчетных и экспериментальных значений не превышает 4%.

Следующий этап расчета – определение параметров движения элементов загрузки по наклонному статическому кольцу.

Уравнения движения для него:

⁽²⁾

Расчет по уравнения (2) проводился для мельницы с диаметром ротора d_р = 0,2 до 1,0 м и угол наклона образующей кольца α = 15 − 75°. Начальными условиями для расчета являлись значения координат тела и скоростей по осям r, φ и z на выходе из ротора. Граничным условием при расчете принималось v_rz = 0.

В результате расчета было установлено, что максимальное радиальное перемещение возрастает с увеличением диаметра ротора, что объясняется увеличением центробежной силы на выходе из ротора. Аналогичная закономерность наблюдается и при уменьшении угла наклона между образующей конического кольца (рис. 3), причем изменение угла в пределах от 45 до 75° не очень существенно влияет на изменение радиального перемещения.

Перекатывающееся по поверхности кольца измельчающее тело (шар) перемещается в радиальном направлении на значительно большее расстояние, чем скользящая частица материала. Поскольку при измельчении необходим контакт материала и мелющих тел, то максимальный радиус кольца ограничивается радиальным перемещением r_max частиц материала.

Вместе с тем для полного использования поверхности кольца необходимо, чтобы площадь его поверхности была приблизительно равна площади внутренней поверхности ротора.

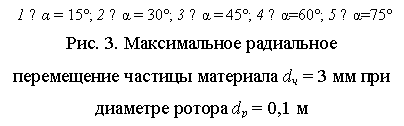При этом мелющие тела, соприкасающиеся непосредственно со стенками ротора (первый слой), вытесняться на поверхность кольца, а остальные займут их место и обеспечат соударения между телами, скатывающимися с кольца и находящимися на роторе.

Заключение. Предложенная методика расчета, базирующаяся на решении системы дифференциальных уравнений, является одной из составных частей общей методики расчета траектории движения мелющих тел внутри мельницы. Она дает возможность определить: высоту подъема в зависимости от угловой скорости и конструкционных параметров мельницы, а по высоте подъема материала − максимально возможную высоту цилиндрической части ротора мельницы; максимальное радиальное перемещение элементов загрузки и максимально возможный радиус кольца, с учетом угла наклона его образующей и линейной скорости ротора.

Литература:

1. Вайтехович, П. Е. Определение важнейших параметров центробежно-шаровых мельниц / П. Е. Вайтехович, В. С. Францкевич, Г. М. Хвесько // Химическое и нефтегазовое машиностроение. − 2007. − № 10. – С. 3 − 5.

2. Боровский, Д. Н. Математическое моделирование движения мелющих тел на роторе вертикальной центробежной мельницы / Д. Н. Боровский, П. Е. Вайтехович, Д. В Семененко // Труды БГТУ. Сер. III, Химия и технология неорган. в-в. – 2009. – Вып. XVII. – С. 163 – 166.