МАТЕМАТИКА/3.Теория вероятностей и математическая статистика

к.ф.-м.н. Искакова А. С., Шалкенов Ж.Е.

Евразийский национальный книверситет имени Л.Н. Гумилева, Астана, Казахстан

Построение множества несмещенных оценок распределения сумм случайных величин, при ненаблюдаемых элементах выборки

Многомерные вероятностные модели, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни. В последние годы было разработано значительное количество вероятностных моделей. Тем не менее остается много не решенных проблем, когда пронаблюдать возможно только суммы компонентов, которые в результате наблюдений невозможно выявить. До настоящего времени вероятностные модели, описывающие подобные ситуации, не рассматривались. Исключительным актуальным примером применения подобной модели является рекламная индустрия, когда необходимо увязать распределение потребительских интересов с соответствующей рекламой в различных источниках. Аналогичные проблемы очень часто встречаются в метеорологии и в других областях. В этой работе представляются статистические оценки распределения сумм случайных значений L₁, … , L_d, когда L₁, … , L_d не наблюдаемы, а наблюдаемы только их суммы. Тем самым результаты предложенной работы позволяют решить многие из вышеперечисленных проблем.

Предположим, что урна содержит шары, и каждый шар в урне помечен некоторым значением L_α. Также допустим, что число возможных L_α есть d.

Пусть элементы вектора p=(p₁, … , p_d) определяют вероятности извлечения из урны шара, помеченного соответственными значениями L₁, … , L_d, причем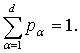

Производится последовательное извлечение n шаров из урны с возвращением, причем неизвестно, какие именно шары были вынуты из урны. Известно только значение u, которое представляет сумму значений на n вынутых из урны шаров. Для изучения данной ситуации требуется построение распределения вероятности u.

Допустим, что V_u представляет число возможных сочетаний r_1vuL₁,…, r_{d vu}L_d, которые в сумме образовали u, где r_1vu,…, r_dvu определяют возможное количество вынутых шаров, которые помечены соответствующими L₁, … , L_d. Иначе говоря, из работы [1] следует, что V_u есть число разбиений u на части L₁,…, L_d.

Из результатов работ [5-15] следует следующее утверждение. Вероятность, что случайная величина U примет значение u, есть

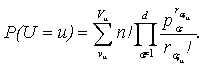(1)

Теорема. Функция, которая определяется в (1.1), является распределением вероятностей.

Пусть Х=(X₁, ..., X_k) представляет выборку объема k из распределения (1) и х=(x₁, ..., x_k) есть наблюдавшиеся значения Х, где элементы х_i (i=1, …, k) представляют сумму значений на n шарах, последовательно вынутых из урны с возвращением. Для каждого i=1, ..., k определим V_i число разбиений х_i на значения L₁, … ,L_d. Векторы r_1i=(r_11i,…, r_d1i), …, r_Vi=(r_1Vi,…, r_dVi), определяющие эти разбиения, при v_i=1,..., V_i, являются решениями следующей системы уравнений

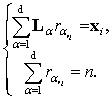(2)

Пусть для каждого j=1,…, μ, где 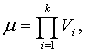существует вектор z_j=(z_1j,..., z_dj), определяемый как 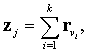причем индексы в правой и левой части связаны между собой взаимно однозначным соответствием, которое не единственно.

Лемма. a) Если какой – то элемент реализации выборки х=(x₁, ... , x_k) из распределения (1) имеет более одного разбиения на представленные части, то решения z₁, … , z_μ, основанные на наблюдении, не являются реализациями достаточных статистик.

b) Если все элементы реализации выборки х=(x₁, ... , x_k) из распределения (1) имеют не более одного разбиения на представленные части, то решение z₁, основанное на наблюдении, является единственным и представляет реализацию полной достаточной статистики.

Следующая теорема, приводимая в работах [6-9], позволяет определить множество несмещенных оценок для вероятности исследуемого распределения.

Теорема. Элементы множества W(u, z)={W(u, z₁), …, W(u, z_μ)} являются несмещенными оценками для вероятности P(U=u) распределения (1.1), которые при j=1, …, μ определяются как

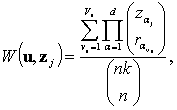(3)

где V_u –число разбиений u на части L₁,…, L_d; для каждого разбиения r_1vu,…, r_dvu определяют возможное количество вынутых шаров, которые помечены соответствующими L₁, …, L_d; k≥1 и z_αj≥r_αvu, при α=1, …, d, v_u=1, …, V_u.

Рассмотрим следующие следствия данной теоремы.

Список литературы

1. Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез.– М.: Наука. 1984.– 472 c.

2. Боровков А.А. Теория вероятностей.- М.: Наука. 1986.–431 с.

3. Воинов В.Г., Никулин М.С. Несмещенные оценки и их применения.– М.: Наука. 1989. – 440 с.

4. Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высшая школа. 1984. – 248 с.

5. Искакова А.С. Об одном классе многомерных дискретных распределений, порождаемых урновой схемой с шарами, помеченными прямоугольными матрицами. // Вестник КазГУ, сер. матем., мех., информатика. 2000 г. №1(94). С. 16-20.

6. Искакова А.С. Построение несмещенных оценок вероятностей распределения сумм независимых одинаково распределенных случайных матриц. // Вестник КазГУ, сер. матем., мех., информатика. 2001 г. №4(97). С. 16-20.

7. Искакова А.С. Об одном методе статистического оценивания вероятности оправдываемости прогноза в метеорологии. // Научный журнал Министерства образования и науки Республики Казахстан “Iзденiс” – “Поиск”, сер. естественных наук. 2001 г. № 4, 5. С.182-188.

8. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

9. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.