МАТЕМАТИКА/3.Теория вероятностей и математическая статистика

к.ф.-м.н. Искакова А. С., Шалкенов Ж.Е.

Евразийский национальный книверситет имени Л.Н. Гумилева, Астана, Казахстан

Несмещенное оценивание вероятности распределения сумм случайных величин при не наблюдаемых элементах выборки с хорошими асимптотическими свойствами

Многомерные вероятностные модели, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни. В последние годы было разработано значительное количество вероятностных моделей.

Предположим, что урна содержит шары, и каждый шар в урне помечен некоторым значением L_α. Также допустим, что число возможных L_α есть d.

Пусть элементы вектора p=(p₁, … , p_d) определяют вероятности извлечения из урны шара, помеченного соответственными значениями L₁, … , L_d, причем Производится последовательное извлечение n шаров из урны с возвращением, причем неизвестно, какие именно шары были вынуты из урны. Известно только значение u, которое представляет сумму значений на n вынутых из урны шаров. Для изучения данной ситуации требуется построение распределения вероятности u.

Допустим, что V_u представляет число возможных сочетаний r_1vuL₁,…, r_{d vu}L_d, которые в сумме образовали u, где r_1vu,…, r_dvu определяют возможное количество вынутых шаров, которые помечены соответствующими L₁, … , L_d. Иначе говоря, из работы [1] следует, что V_u есть число разбиений u на части L₁,…, L_d. Из результатов работ [5-15] следует следующее утверждение. Вероятность, что случайная величина U примет значение u, есть

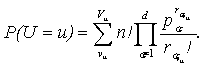(1)

Теорема. Функция, которая определяется в (1), является распределением вероятностей.

Пусть Х=(X₁, ..., X_k) представляет выборку объема k из распределения (1) и х=(x₁, ..., x_k). Векторы r_1i=(r_11i,…, r_d1i), …, r_Vi=(r_1Vi,…, r_dVi), определяющие эти разбиения, при v_i=1,..., V_i, являются решениями следующей системы уравнений

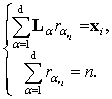(2)

Пусть для каждого j=1,…, μ, где 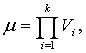существует вектор z_j=(z_1j,..., z_dj), определяемый как 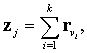причем индексы в правой и левой части связаны между собой взаимно однозначным соответствием, которое не единственно.

Лемма. a) Если какой – то элемент реализации выборки х=(x₁, ... , x_k) из распределения (1) имеет более одного разбиения на представленные части, то решения z₁, … , z_μ, основанные на наблюдении, не являются реализациями достаточных статистик.

b) Если все элементы реализации выборки х=(x₁, ... , x_k) из распределения (1) имеют не более одного разбиения на представленные части, то решение z₁, основанное на наблюдении, является единственным и представляет реализацию полной достаточной статистики.

Следующая теорема, приводимая в работах [6-9], позволяет определить множество несмещенных оценок для вероятности исследуемого распределения.

Теорема. Элементы множества W(u, z)={W(u, z₁), …, W(u, z_μ)} являются несмещенными оценками для вероятности P(U=u) распределения (1.1), которые при j=1, …, μ определяются как

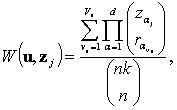(3)

где V_u –число разбиений u на части L₁,…, L_d; для каждого разбиения r_1vu,…, r_dvu определяют возможное количество вынутых шаров, которые помечены соответствующими L₁, …, L_d; k≥1 и z_αj≥r_αvu, при α=1, …, d, v_u=1, …, V_u.

Рассмотрим следующие следствия данной теоремы.

Имеем множество несмещенных оценок (3) для вероятности распределения (1). Рассмотрим задачу определения наиболее подходящей несмещенной оценки. Из решения системы уравнений (2) видно, что при i=1,…, k величина x_i разбивается на L₁,…, L_d V_i³1способами. В случае, если V_i>1, то не известно, каким вариантом v_i=1, …, V_i сложений произведений на соответствующих значениях r_1vi, … , r_dvi получили величину x_i. В связи с этим, имеем множество решений основанных на наблюдении, и множество несмещенных оценок для вероятности распределения (1.1) Для определения наиболее подходящего решения z_g из множества z и соответствующей оценки W(u, z_g) из множества несмещенных оценок W(u, z) рассмотрим следующие определения, приводимые в работах [6-9].

Определение. Решение z_g, основанное на наблюдении, является наиболее подходящим из множества z={z₁, … , z_m}, если

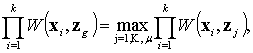(4)

где при i=1, … , k элементы множества W(x_i, z)={ W(x_i, z₁), … , W(x_i, z_m)} являются несмещенными оценками для вероятности P(U=u) распределения (1), определенными в (3).

Определение. Несмещенная оценка W(u, z_g) для вероятности P(U=u) распределения (1) является наиболее подходящей из всего множества несмещенных оценок

W(u, z)={ W(u, z₁), … , W(u, z_m)},

определяемых в (3), если z_g – наиболее подходящее решение, основанное на наблюдении.

Следующее замечание, приводимое в работах [6-9], указывает на асимптотические свойства наиболее подходящих несмещенных оценок.

Теорема. Наиболее подходящая несмещенная оценка W(u, z_g) для вероятности P(U=u) модели (1) является состоятельной, асимптотически нормальной и асимптотически эффективной.

Анализ проведенных в настоящей работе исследований позволяет сформулировать следующие основные результаты.

1. Предложено и изучено новое распределение вероятностей, порождаемых урновой схемой с шарами, помеченными числами, в случае когда наблюдаемы только их суммы.

2. Получено множество несмещенных оценок для распределения вероятностей предлагаемой модели и дисперсии этих оценок.

3. Введено новое понятие наиболее подходящей оценки из множества несмещенных оценок, обладающих асимптотическими свойствами.

Список литературы

1. Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез.– М.: Наука. 1984.– 472 c.

2. Боровков А.А. Теория вероятностей.- М.: Наука. 1986.–431 с.

3. Воинов В.Г., Никулин М.С. Несмещенные оценки и их применения.– М.: Наука. 1989. – 440 с.

4. Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высшая школа. 1984. – 248 с.

5. Искакова А.С. Об одном классе многомерных дискретных распределений, порождаемых урновой схемой с шарами, помеченными прямоугольными матрицами. // Вестник КазГУ, сер. матем., мех., информатика. 2000 г. №1(94). С. 16-20.