Изучение формул квадриад
Евсеев В.И, канд. физ.-мат. наук, доцент,
г.
Казань, РТ
УДК 681.32
Аннотация:
Квадриады представляют
собой логические фигуры, из которых
составлена игра в тетрис. В
предлагаемых заметках изучается теоретическая основа этой модели на базе
классической логики.
Ключевые слова: фигура,
позиция фигуры, логическая матрица, ее
линии, бинарные операции над фигурами.
Summary: The Kvadriady are logical form, which is the game of
Tetris. The notes proposed examines the
theoretical basis of this model based on classical logic. Keywords: figure, the
position of a shape, a logical matrix, its lines, binary operations on Forms.
Вид фигур квадриад
хорошо известен, так как они составляют основу игры в тетрис. Поэтому сами фигуры
мы демонстрировать в различных позициях не будем, а сразу перейдем к построению
их формул с помощью разработанного автором метода.
1.
Формулы первой фигуры.
Как известно, существует всего пять фигур, состоящих из
четырех клеток одного размера, каждую из них мы погружаем в соответствующий по
размерам полигон (прямоугольник) так, чтобы
фигура в данной позиции помещалась в нем вместе со своей оболочкой, и
при этом некоторые клетки могут оставаться пустыми. Логическая матрица строится
по виду фигуры на полигоне. Как мы уже
отмечали, для построения формул логических фигур применяется матричный метод, в
котором участвуют два типа высказываний: ![]() и
и ![]() , а также их отрицания, при этом первые из них
характеризуются вертикальным столбцом значений, а вторые – вертикальной
строкой. Размер стороны квадрата этой матрицы на единицу меньше суммы
размерностей матрицы полигона, то есть, если полигон имеет вид
, а также их отрицания, при этом первые из них
характеризуются вертикальным столбцом значений, а вторые – вертикальной
строкой. Размер стороны квадрата этой матрицы на единицу меньше суммы
размерностей матрицы полигона, то есть, если полигон имеет вид ![]() , то размер квадрата логической матрицы равен:
, то размер квадрата логической матрицы равен: ![]() . (1)
. (1)
Прежде всего, в этой матрице выделяется правый
нижний блок, соответствующий изображению вмещающего полигона фигуры с ее
оболочкой в рассматриваемой позиции, затем строятся «несущие» вертикальные и
горизонтальные значения логических переменных (![]() ,
,![]() ), после этого диагональным методом в левом нижнем блоке
изображаются переменные типа
), после этого диагональным методом в левом нижнем блоке
изображаются переменные типа ![]() , причем четные ставятся сразу с
отрицаниями . Затем устанавливаются высказывания типа
, причем четные ставятся сразу с
отрицаниями . Затем устанавливаются высказывания типа ![]() в вернем правом блоке, также с учетом отрицания по четным
значениям. В самом изображении полигона выделенная серым цветом на изображении
позиции фигура отмечается единицами, клетки оболочки указываются нулями, а
пустые клетки (если они имеются) отмечаются символом пустого множества и в
дальнейшем анализе участия не принимают.
в вернем правом блоке, также с учетом отрицания по четным
значениям. В самом изображении полигона выделенная серым цветом на изображении
позиции фигура отмечается единицами, клетки оболочки указываются нулями, а
пустые клетки (если они имеются) отмечаются символом пустого множества и в
дальнейшем анализе участия не принимают.
Мы применяем методику «больших матриц» (см. ![]() ,
которая в данном случае оказывается эффективной.
,
которая в данном случае оказывается эффективной.
Для первой позиции линейной триады ![]() ,
которая изображается горизонтально и погружается в полигон
,
которая изображается горизонтально и погружается в полигон ![]() получаем логическую матрицу:
получаем логическую матрицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Напомним, что последовательные пары строк этой
матрицы составляют линию.
Для данной матрицы строит две ее линии:
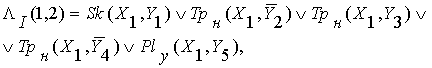 (1.1)
(1.1)
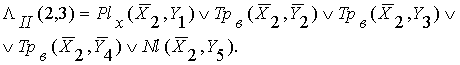 (1.2)
(1.2)
Для вертикальной позиции этой фигуры ![]() получаем
матрицу:
получаем
матрицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
0 |
0 |
Так в этой матрице мы получаем пять линий: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . Каждая линия представляет собой композицию бинарных
операций. Например, для этого случая мы получаем:
. Каждая линия представляет собой композицию бинарных
операций. Например, для этого случая мы получаем:
![]() ,
(1.3)
,
(1.3)
![]() =
= ![]() , (1.4)
, (1.4)
![]() =
= ![]() , (1.5)
, (1.5)
![]() =
= ![]() , (1.6)
, (1.6)
![]() =
= ![]() . (1.7)
. (1.7)
Вся формула этой позиции имеет вид дизъюнкции
этих формул по линиям:
![]()
![]()
![]() (1.8)
(1.8)
2.
Формулы второй фигуры.
Вторая фигура не имеет осей симметрии, поэтому
допускает восемь различных позиций. В
данном случае исходная позиция приводит к логической матрице:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
0 |
Ø |
Ø |
Эта матрица имеет три линии, которые можно сразу
записать:
![]() , (2.1)
, (2.1)
![]() (2.2)
(2.2)
![]() =
= ![]() . (2.3)
. (2.3)
Вторая позиция этой фигуры ![]() приводит к логической матрице:
приводит к логической матрице:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
Ø |
|
|
|
|
1 |
0 |
1 |
0 |
Ø |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
Значит, эта матрица имеет четыре линии, которые
определяют формулы:
![]() , (2.4)
, (2.4)
![]() =
=![]() , (2.5)
, (2.5)
![]() =
= ![]() (2.6)
(2.6)
![]() =
=![]() .
(2.7)
.
(2.7)
Следующая позиция ![]() имеет
такую логическую матрицу:
имеет
такую логическую матрицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
Ø |
Ø |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
Значит, она имеет три линии, которые составляют
формулы:
![]() , (2.8)
, (2.8)
![]() =
=![]() (2.9)
(2.9)
![]() =
=![]() (2.10)
(2.10)
Четвертый случай позиции для второй фигуры ![]() приводит к матрице:
приводит к матрице:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
1 |
Ø |
0 |
1 |
0 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
Таким образом, получаем формулы линий этой
матрицы:
![]() (2.11)
(2.11)
![]() =
=![]() (2.12)
(2.12)
![]() =
=![]() , (2.13)
, (2.13)
![]() =
=![]() . (2.14)
. (2.14)
Теперь
получаем матрицу ![]() ,
погруженную в полигон
,
погруженную в полигон ![]() которая
имеет три линии.
которая
имеет три линии.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
1 |
Ø |
Ø |
0 |
0 |
0 |
Эта матрица позволяет найти формулы ее линий:
![]() (2.15)
(2.15)
![]() =
=![]() (2.16)
(2.16)
![]() =
=![]() . (2.17)
. (2.17)
Позиция ![]() позволяет построить
матрицу:
позволяет построить
матрицу:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
Ø |
|
|
|
|
0 |
0 |
0 |
0 |
Ø |
Для этой матрицы находятся формулы ее четырех
линий:
![]() (2.18)
(2.18)![]() (2.19)
(2.19)
![]()
![]() , (2.20)
, (2.20)
![]() =
= ![]() . (2.21)
. (2.21)
Следующая позиция ![]() получается
также поворотом:
получается
также поворотом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
Ø |
Ø |
|
|
|
1 |
0 |
1 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
На ее основе находим формулы линий:
![]() (2.22)
(2.22)![]() (2.23)
(2.23)
![]()
![]() (2.24)
(2.24)
Для позиции
![]() находим логическую
матрицу:
находим логическую
матрицу:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
|
|
|
|
1 |
Ø |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
Теперь получаем формулы четырех линий этой
матрицы:
![]() (2.25)
(2.25)
![]() (2.26)
(2.26)
![]() (2.27)
(2.27)
![]() =
=![]() (2.28)
(2.28)
3.
Формулы третьей фигуры.
Для
первой позиции третьей фигуры ![]() квадриад находим матицу:
квадриад находим матицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
Ø |
0 |
0 |
0 |
Ø |
|
|
|
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
Здесь мы получаем три логических линии, дизъюнкция
которых составляет формулу всей фигуры.
![]() (3.1)
(3.1)
![]() =
=![]() (3.2)
(3.2)
![]() =
=![]() (3.3)
(3.3)
Заметим, что эта фигура обладает симметрией,
поэтому имеет только четырех позиции.
В результате поворота из первой позиции следует
вторая ![]() :
:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
Запишем
формулы ее четырех линий:
![]() (3.4)
(3.4)
![]() =
=![]() (3.5)
(3.5)
![]() =
=![]() (3.6)
(3.6)
![]() =
=![]() . (3.7)
. (3.7)
После
поворота получаем следующую позицию ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
0 |
|
0 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
1 |
Ø |
0 |
0 |
0 |
Ø |
В
данном случае формула этой фигуры имеет
три линии:
![]() (3.8)
(3.8)
![]() =
=![]() (3.9)
(3.9)
![]() =
=![]() (3.10)
(3.10)
Последняя возможная позиция ![]() этой фигуры получается из предыдущей позиции
также путем поворота:
этой фигуры получается из предыдущей позиции
также путем поворота:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
Ø |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
|
0 |
0 |
Ø |
Следовательно,
формула здесь характеризуется четырьмя линиями:
![]() (3.11)
(3.11)
![]() =
=![]() (3.12)
(3.12)
![]() =
=![]()
![]() =
= ![]() (3.13)
(3.13)
4.
Формула четвертой
фигуры.
Эта фигура обладает двумя осями симметрии,
поэтому у нее только одна допустимая позиция![]() ,
для которой и составляется матрица:
,
для которой и составляется матрица:
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
0 |
0 |
0 |
Логические
линии здесь имеют вид:
![]() (4.1)
(4.1)
![]() =
=![]() (4.2)
(4.2)
![]() =
=![]() (4.3)
(4.3)
Напомним, что вся формула фигуры является
дизъюнкцией формул этих линий,
и мы можем, в принципе, найти область истинности
каждой фигуры. Эти вопросы мы оставляем для следующего, более объемного труда.
5.
Формулы пятой фигуры.
Пятая фигура допускает четыре позиции,
рассмотрим их формулы.
Для первой позиции ![]() получаем
матрицу:
получаем
матрицу:
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
Ø |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
Ø |
0 |
0 |
0 |
0 |
По этой матрице находим формулы ее линий:
![]() (5.1)
(5.1)
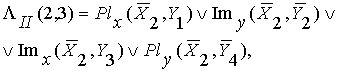 (5.2)
(5.2)
![]() =
=![]() (5.3)
(5.3)
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
Ø |
Вторая позиция ![]() имеет такую логическую матрицу:
имеет такую логическую матрицу:
Здесь формулы логических линий имеют вид:
![]() (5.4)
(5.4)
![]() =
=![]() (5.5)
(5.5)
![]() (5.6)
(5.6)
![]() =
= ![]() (5.7)
(5.7)
Следующая позиция ![]() получается симметрией из
начального вида:
получается симметрией из
начального вида:
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
0 |
0 |
Ø |
Таким образом, находим здесь формулы логических
линий матрицы:
![]() (5.8)
(5.8)
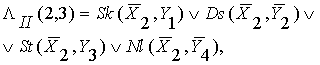 (5.9)
(5.9)
![]() (5.10)
(5.10)
Перейдем к последней
возможной позиции ![]()
Так мы получаем
логическую матрицу
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
Ø |
|
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
Ø |
0 |
0 |
0 |
Поэтому определяются линии этой матрицы:
![]()
![]()
![]()
![]() =
= ![]()
Таким образом, мы
получили все формулы для логических матриц различных возможных позиций
квадриад.
Из этих результатов
всегда можно определить области истинности каждой логической линии,
следовательно, и каждой формулы изучаемой фигуры.
Литература:
1. Евсеев В.И.
Конструктивная комплементарная семантика. Монография. Изд-во «Ламберт». 2014
г.2.
2. Евсеев В.И. Аспекты
информознания //Труды международной научно-практической конференции «Новости
передовой науки». Т.12 . 2014 г.(63-74).