к.ф.-м.н. Кулиш О.А., к.т.н. Шарифуллин С.Р., д.т.н. Хисамов Ф.Г.

Военная академия связи (филиал, г. Краснодар), Россия

Моделирование распределения электромагнитного поля в оптоволокне

Характерной чертой информационной эры является бурное развитие коммуникаций - одной из составляющих инфраструктуры информационных технологий. В условиях возросшей потребности в обеспечении надежного канала связи, как в сфере построения глобальных информационных сетей, так и в области промышленной автоматизации возникла необходимость поиска альтернативных технологий передачи данных взамен традиционных. Оптическое волокно в настоящее время считается самой совершенной физической средой для передачи информации, а также самой перспективной средой для передачи больших потоков информации на значительные расстояния.

Для моделирования электромагнитного поля оптической волны в волокне необходимо решить волновое уравнение. Уравнения Максвелла с учетом гармонической зависимости и от t запишутся в виде:

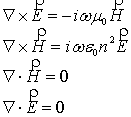
Для анализа изгибов волноводов удобнее использовать цилиндрические координаты , , . Ввод цилиндрической системы координат для изгиба волновода представлен на рисунке 1.

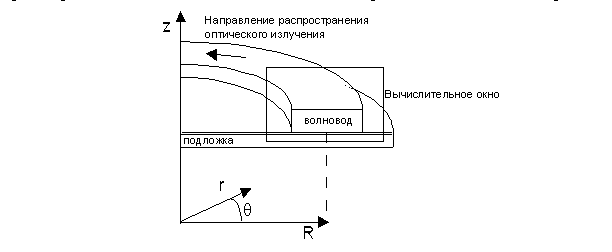
Рис. 1 Трехмерный оптический волновод в цилиндрической системе координат

Используя формулу ротора в цилиндрических координатах и представляя компоненты в виде , , , где - угловая константа распространения, из уравнений Максвелла получим волновое уравнение в цилиндрических координатах для ТЕ - моды:

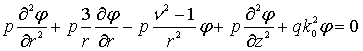
где , , .

Точного решения волновое уравнение не имеет, поэтому возникает необходимость провести анализ электромагнитного поля в световоде подходящим численным методом - методом конечных элементов.

Для решения данного уравнения производится разбиение поперечного сечения реального оптического волновода на некоторое конечное число простых симплекс-элементов, внутри которых поля представляются полиномами, а показатель преломления считается постоянным [1]. Наиболее часто для такого разбиения применяют триангуляцию (разделение на треугольники). Пример триангуляции области приведен на рисунке 2. Для этого метода существуют программы триангуляции, встроенные в системы САПР. При адаптивном разбиении области в тех ее частях, где необходим более тщательный анализ, сетка разбиения может быть сделана гуще.

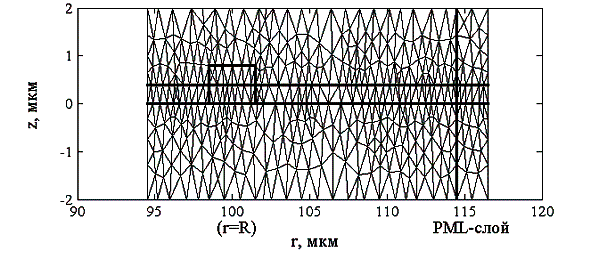
Рис. 2 Адаптивная триангуляция вычислительного окна

Решение данного волнового уравнения в цилиндрических координатах заменим вариационной задачей, т.е. с помощью вариационного исчисления дифференциальному волновому уравнению поставим в соответствие на области Ω функционал

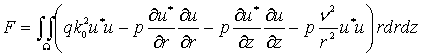
Функция на каждом элементе разбиения представляется в виде аппроксимации:

,

где - вектор значений функции u в узлах треугольного элемента, - вектор весовых функций второго порядка, введенных через - координаты для треугольных элементов. Чтобы избежать изменения границ интегрирования при переходе от одного элемента к другому, вводят различным образом систему координат , связанную с каждым конкретным элементом [2]. Координатные переменные представляют собой базисные функции первого порядка для треугольного элемента. Подставив аппроксимацию функции в функционал , исследуют его на минимум, т.е. находят частные производные по значениям и приравнивают их нулю. При этом функционал рассматривается как функция коэффициентов . Получим систему уравнений:

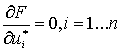
Если ввести коэффициенты:

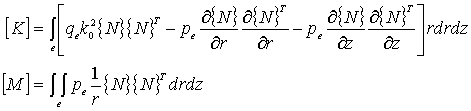
то система уравнений приводится к виду:

Полученная система уравнений является задачей на собственные значения. Матрицы и называются матрицами жесткости для одного элемента. Эти матрицы формируются из коэффициентов при

Матрица жесткости, полученная данным методом, содержит в себе информацию о распределении поля только в пределах конкретного элемента. Для нахождения поля на выбранной области, включающей в себя все элементы разбиения, необходимо составить общую матрицу, которая определяла бы значения электрического поля на всей области распределения. Для этого составляют глобальную матрицу А. В результате процесса ансамблирования получается обобщенная задача на собственные значения, которую в общем случае можно записать в виде:

где искомые величины: - вектор-столбец, связанный со значениями электрического поля в узлах сетки, - угловая константа распространения волны.

Решая данную матричную задачу, получаем информацию о модовом составе волновода. Зная распределение напряженности по сечению волновода можно рассчитать мощность моды и ее потери [3]. Оценка уровня радиационных потерь оптического сигнала в изогнутом волноводе является важной, так как накладывает ограничения на параметры волноводной структуры оптических устройств в волоконных линиях связи.

Литература

1. Гуртов В.А. Оптоэлектроника и волоконная оптика: учеб. пособие. Петрозаводск: Изд-во ПетрГУ, 2007. - 243 с.

2. Paul Polishuk, Ph.D. Plastic Optical Fibers Branch Out. Plastic Optical Fiber Trade Organization (POFTO). May 30, 2006. URL: <http://www.pofto.com/downloads/ieee/pof.branches.v6.pdf>.

3. Гришачев В.В., Кабашкин В.Н., Фролов А.Д. Анализ каналов утечки информации в волоконно-оптических линиях связи: нарушение полного внутреннего отражения. URL: http://www.contrterror.tsure.ru