Математика/5.Математическое моделирование.

К.ф.-м.н.Искакова А.С.,Токсанова С.С.

Евразийский национальный университет имени Л.Н. Гумилева , Астана , Казахстан

Построение критериев ожидаемых прогнозов социальных выплат на случай утраты трудоспособности

Как известно, значения эмпирических формул, в основном, в какой-то степени расходятся с фактическими данными. Например, в таблице 1 показаны расхождения значений эмпирической функций от данных консалтинговых отчетов социальных выплат на случай утраты трудоспособности.

Таблица 1. Значения эмпирической функций и данных консалтинговых отчетов социальных выплат на случай утраты трудоспособности.

Годы	Консалтин отчет	Значение.эмпирическрой функциии	Погрешность
2005	6,2	-180	186
2006	129	-180	309
2007	410,5	-180	591
2008	926,7	-180	1107
2009	1441,6	-180,1	1622
2010	2061,3	-180,1	2241
2011	2780,8	-180,1	2961
2012	3608,90	-180,1	3789
2013	4910,3	-180,1	5090

Как видно, мало вероятно построение идеального прогноза социальных выплат. Отметим, что значения эмпирической функции представляют собой средняя ожидаемая выплата или эффективность операции. Тогда риском r_i операции является модуль разности ожидаемых выплат q_i и значения эмпирической функции y_i, то есть r_i =|q_i -y_i|.

По правилу Вальда или по правилу крайнего пессимизма за рекомендуемый прогноз выплат следует принять прогноз со значением

.

Так, например, при рассмотрении прогноза выплат по потери трудоспособности r₁ =6,199501, r₂ =128,9995, r₃ = 410,4995,…, r₉₌ 4910,3

и . Значит, правило Вальда рекомендует принять прогноз выплат в виде . Ниже в таблице 4 приведены значения рекомендуемых прогнозов по правилу Вальда.

Таблица 2. Крайне пессимистические прогнозы выплат на случай утраты трудоспособности

Годы	2005	2006	2007	2008	2009	2010	2011	2012	2013
Крайне пессимистические прогнозы выплат	-4904,1	-4781,3	-4499,8	-3983,6	-3468,7	-2849	-2129,5	-1301,4	0,000497

Аналогично правилу Вальда можно определить крайние оптимистические прогнозы как

.

Так, например, при рассмотрении прогноза выплат по потери трудоспособности имеем r₁ = 6,199501, r₂ = 128,9995, r₃ = 410,4995,…, r₉₌ 4910, . Значит, крайне оптимистические прогнозы получаемые значения как , приведены в таблице 3.

Таблица 3. Крайне оптимистические прогнозы выплат на случай утраты трудоспособности

Годы	2005	2006	2007	2008	2009	2010	2011	2012	2013
Крайне оптимистические прогнозы выплат	4916,5	5039,3	5320,8	5837	6351,9	6971,6	7691,1	8519,2	9820,6

Таким образом, по результатам данных в таблиц 2 и 3 имеем следующие графики, описывающие эмпирические функции, функции крайних пессимистических и оптимистических прогнозов выплат.

Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат от утраты трудоспособности изображены на рисунке 1, где Ряд 1- функция крайних пессимистических прогнозов, Ряд 2- эмпирическая функция , Ряд 3-функция крайних оптимистических прогнозов.

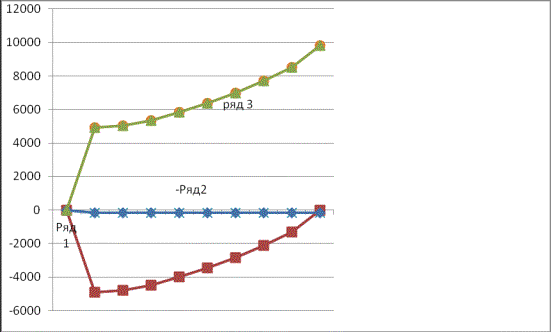
Рисунок 1. Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат от утраты трудоспособности

Очевидно, что значение прогноза выплат , принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов, удовлетворяет следующему условию или

.

Таким образом, значение прогноза выплат на случай утраты трудоспособности, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов, удовлетворяет следующему условию

Значение прогноза выплат на случай потери кормильца, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов, удовлетворяет следующему условиям

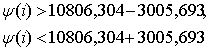
Список литературы

1. Данилина Н.И. и др. Численные методы.

2. Малыхин В.И. Финансовая математика. –М.:Юнити, 2003. -237 с.

3. Волков И., Загоруйко Е. Исследование операций. М-2002.

4. Ледерман Э., Справочник по прикладной статистике т.2, – М., Финансы и статистика. 1990