Педагогические науки, современные методы преподавания

К.ф.м.-н. доцент Жураев И.М., преподаватель Шарипова И.Ф. Преподаватель Жураев Ф. М.

Бухарский Государственный Университет, Узбекистан

Приложения определенного интеграла

Геометрические применения определенногоинтеграла.

Площадь криволинейной трапеции, т. е. площадь фигуры ограниченной графиком на сегменте непрерывной и неотрицательной функции , ординатами, проведенными в точках и , и отрезком оси между точками и , находится по формуле:

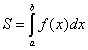. (1)

Если плоская фигура ограничена прямыми и кривыми , причем , то ее площадь вычисляется по формуле

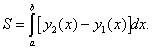(2)

В отдельных случаях левая граница (или правая граница ) может выродиться в точку пересечения кривых и В этих случаях величины и отыскиваются как абсциссы точек пересечения указанных кривых.

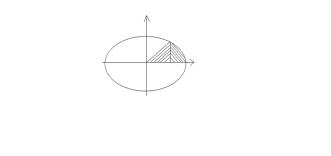
Пример 1. Даны эллипс и точка на нем (рис.1). Определить плошадь криволинейной трапеции и сектора.

M

O

B

K

0

Рис. 1

Решение. Из уравнения эллипса имеем ,

так что по формуле (1)

K

пл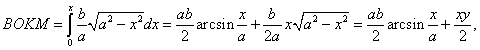

Так как последнее слагаемое представляет площадь , то, отнимая ее, для площади сектора получим выражение

пл.

При для площади четверти эллипса найдем значение так что площад всего эллипса Для круга и получается известная формула

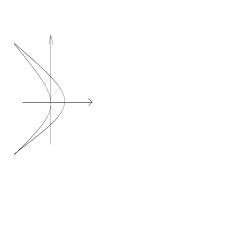
Пример 2. Вычислить площадь фигуры, ограниченной параболами (рис. 2).

Y

Решение. Решая систему уравнение

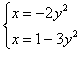, найдем ординаты точек пересечения кривых Так как при то по формуле (2) имеем

.

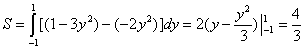Литература

1. Демидович В.П. Сборник задач по математическому анализу. М.»Наука» 1990.

2. Кудрявцев Л.Д.Курс математического анализа 1,2 т. М.»Высшая школа» 1981.

3. Фихтенгольц Г.М . Курс дифференциального и интегрального исчесления 1,2,3 т.М. «Наука» 1970