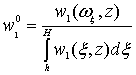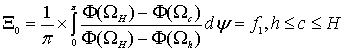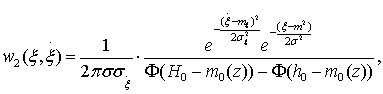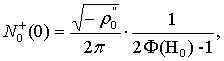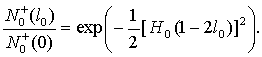Д.т.н. Сальников А.Н., к.т.н. Котина Н.М., асс. Вавилина Н.А.

Саратовский государственный технический

университет имени Гагарина Ю.А., 410054 г. Саратов, Россия

Параметры шероховатости поверхности

с гармоническим трендом (одномерная теория)

1. Общие положения

Почти всегда при определении параметров шероховатой поверхности, которая в общем случае является реализацией некоторой двумерной функции, исходят из весьма общих предположений о распределении материала в шероховатом слое. В большинстве случаев для упрощения задачи считают случайные функции стационарными в широком или в узком смысле и вводят «а priori» закон распределения случайной величины. Уже при таких весьма общих предположениях задача определения параметров шероховатой поверхности становится вполне определенной.

Для того чтобы получить выражения параметров шероховатой поверхности, двумерную случайную функцию, описывающую рельеф любой из контактирующих поверхностей, представим как набор одномерных реализаций (профилограмм) в различных направлениях. Указанный подход позволяет значительно упростить решение задачи, но имеет один существенный недостаток – при построении модели профилограммы имеют дело с характеристиками, которые статистически менее устойчивы к изменению тех или иных условий, чем эквивалентные им характеристики двумерных реализаций. Именно поэтому гистограммы одномерных реализаций, как правило, трудно идентифицировать с каким-либо законом распределения, поскольку они весьма чувствительны к изменению средних значений.

Исследования ряда авторов [1,2] позволяют утверждать, что в качестве модели профилограммы шероховатой поверхности может быть принята функция:

η(z)= ξ₀(z)+ξ(z), (1)

где ξ₀(z) — детерминированная функция, которая может быть как периодической, так и непериодической, ξ(z) — стационарный дифференцируемый случайный процесс с вполне определенным средним значением и автокорреляционной функцией k(z_к), которую можно представить в виде k(z_к)=σ²ρ(z_к), σ ² — дисперсия процесса, ρ(z_к) – нормированная корреляционная функция.

Предположим, что ξ(z) имеет нормальный закон распределения, и определим выражения для плотностей вероятности 1-го и 2-го порядков [3]:

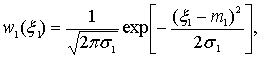(2)

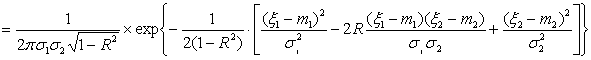. (3)

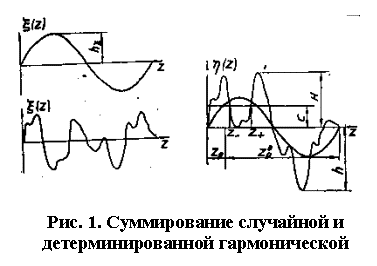
Используя эти выражения, можно найти несколько параметров шероховатой поверхности [2,3], например, среднюю длину контактной линии профиля на уровне с [3], или среднее число положительных и отрицательных пересечений профилограммы с заданной функцией, в частности, с прямой c = const (рис. 1). Перечисленные параметры достаточно полно характеризуют шероховатую поверхность и могут быть использованы для определения кинематических и динамических параметров зоны контакта.

Однако указанные параметры шероховатости при определений их на функциях непрерывного нормального распределения (2) и (3) имеют асимптотический характер. Например, длина контактной линии профиля обращается в нуль только при Н→∞. Принятое же в настоящее время степенное представление длины контактной линии от глубины зацепления контактирующих поверхностей предполагает, что контакт устраняется при вполне определенной конечной величине Н. Более того, при практическом определении характеристик профилограмм всегда используют конечные по длине реализации, на которых при любой детерминированной составляющей абсолютный максимум и абсолютный минимум профилограммы могут быть найдены с вероятностью, равной единице. По этим двум причинам во всех дальнейших расчетах непрерывные распределения (2) – (3) случайной составляющей профилограммы будут заменяться на соответствующие усеченные распределения.

2.Средняя длина контактной линии профиля на заданном уровне.

Пусть детерминированная составляющая профилограммы – периодическая функция периода z

. (4)

Это вполне оправдано, так как обусловлено макроотклонениями формы контактирующих поверхностей от правильной геометрической, функции, описывающие эти отклонения, легко разложимы в ряд Фурье, для которого (4) является одной гармонической составляющей.

На основании сделанных выше замечаний для случайной составляющей профилограммы вместо непрерывного выбираем усеченное распределение, для которого плотность вероятности 1-го порядка имеет вид:

. (5)

После подстановки (2) в (5) и несложных вычислений получим

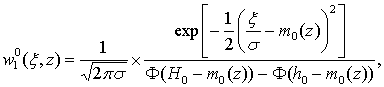(6)

где Ф (z) = 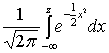— интеграл вероятности,

. (7)

Подставляя (7) и (6) в (8) и учитывая изменение пределов в соответствии с ограничением на функцию (6), получим

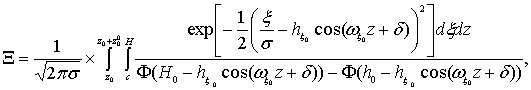(8)

Осуществим в выражении (8) замену переменных .Тогда период подынтегральной функции изменится и станет равным 2π. При этом длина профилограммы z₀ должна быть кратной периоду детерминированной составляющей. Поэтому после соответствующих несложных преобразований, учитывая четность подынтегральной функции, получим:

. (9)

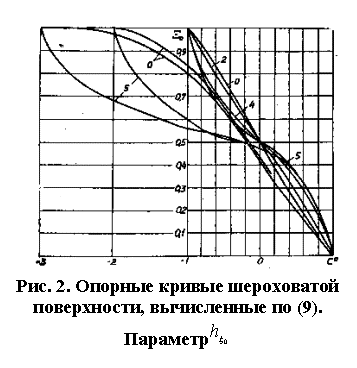
Расчеты по формуле (9) представлены на рис. 2. Если h, Н, →±∞, то усеченный нормальный закон для случайной составляющей переходит в неусеченный, знаменатель подынтегральной функции равенства (9) обращается в единицу и, следовательно,

(10)

Равенство (10) хорошо известно и получено рядом авторов [1, 2] для качественно отличных случайных процессов. Применительно к шероховатой поверхности формула (10) дается в работе [2].

В случае ξ₀(z) = 0 выражение (9) существенно упрощается, так как подынтегральная функция не зависит от :

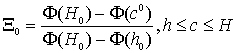(11)

Далее рассмотрим участок с ≈ H, который и определяет контактные свойства шероховатой поверхности. Для его детального описания осуществим в функции (11) замену переменной , которая позволяет перенести начало отсчета функции (11) в точку с = Н. Нормируя l к единице величиной R_z = H–h, получим с/R_z=(Н–l)/R_z. В дальнейшем для упрощения анализа считаем, что Н=–h, т. е. R_z=2H. Тогда с/R_z = ½ – l₀, что после подстановки в (11) приводит к следующей формуле для опорной кривой:

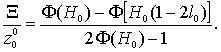(12)

Анализ зависимости (12) позволяет утверждать, что использование широко распространенной степенной аппроксимации опорной кривой в рассматриваемой модели профилограммы возможно только на отдельных достаточно близких к вершине профилограммы участках, причем указанная аппроксимация функцией

. (13)

тем более точна, чем меньше величина Н₀.

3. Расчет среднего числа выступов

шероховатой поверхности над заданным уровнем

В соответствии с общепринятыми представлениями среднее число пересечений профилограммы η(z) с заданной прямой с=const, определяется двумерной совместной плотностью вероятности .

Поскольку случайная составляющая и ее первая производная некоррелированы, то R₁(z) = 0 и, следовательно, величина w₂ может быть представлена как произведение одномерных нормальных плотностей вероятности для профилограммы и ее производной:

(14)

В случае профилограммы с детерминированной гармонической составляющей формула величина перепишется так:

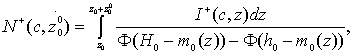(15)

где т₁ = = -ω_ξh_ξ sin(ω_ξz+δ), а

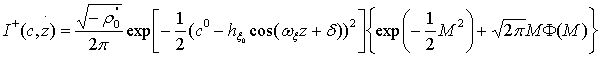. (16)

В соответствии с определениями:

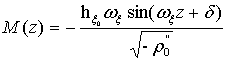. (17)

Подставим (17) и (16) в (15). Учитывая свойства интеграла вероятности и его производной, получим:

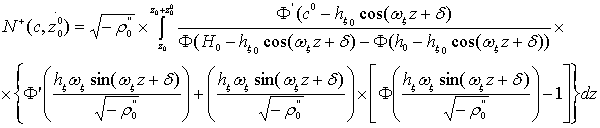(18)

Осуществляя в (18) такую же замену, как и в (8), и проделывая вычисления, ничем не отличающиеся от аналогичных в работе [3], придем к следующему выражению для :

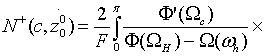
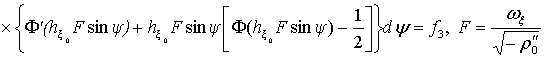. (19)

Из этой формулы легко получаются частные результаты:

а) Асимптотика Н,h→±∞ приводит к известному выражению, описывающему количество перечислений данного уровня с суммой гармонического сигнала и нормального шума [1]:

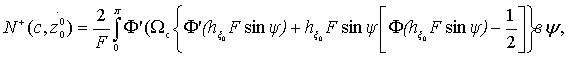(20)

б) При h_ξ0 = 0 имеем

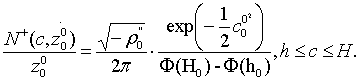(21)

Воспользуемся для анализа выражения (20) той же заменой переменной, что и при анализе формулы (11). В результате получим функцию, определяющую плотность выступов на данном уровне l/R_z:

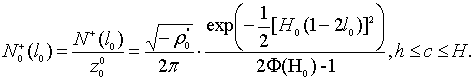(22)

При l₀ =1/2 из формулы (22) получаем распределение плотности нулей профилограммы в зависимости от Н:

(23)

Функция в зависимости от Н₀ показана на рис. 3.

Нормируя плотность выступов на данном уровне (22) плотностью нулей (23), получим следующее выражение:

(24)

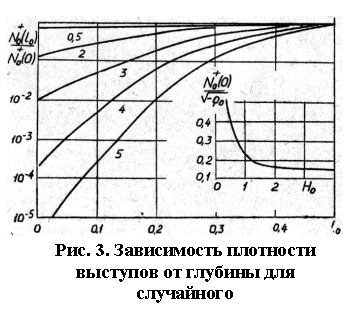
Функция (24) показывает, что для фиксированной величины погружения в шероховатый слой плотность выступов тем больше, чем меньше Н, что также вполне естественно объясняется асимптотикой Н→∞, при которой →0.

4. Теоретическое определение среднего расстояния между выступами

шероховатой поверхности и среднего размера выступа

Для определения параметров ⁺ и ^- используем определяющие их формулы, из которых в соответствии с определением длины контактной линии профиля следует:

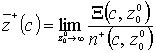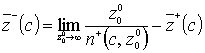, , (25)

В случае, когда – гармоника, а случайная составляющая имеет усеченный нормальный закон распределения, величина описывается формулой (9), из которой следует, что . Учитывая, что

определяется функцией (19), получим:

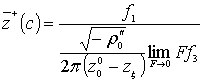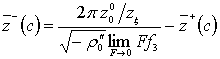, . (26)

Таким образом, вычисление среднего расстояния между выступами и среднего размера выступа в рассматриваемом случае сводится к вычислению , который, как это нетрудно видеть из (19), равен

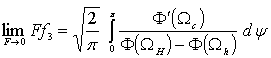. (27)

Подставляя (27) и функцию в (26), получим

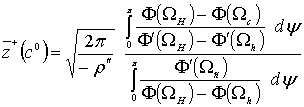,, (28)

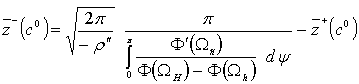, (29)

Традиционная асимптотика Н, после несложных преобразований приводит к известному результату для нормального случайного процесса с неусеченной плотностью. При интегрирование дает π, и приходим к равенствам

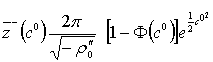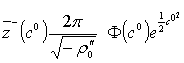, . (30)

При в случае усеченного нормального закона распределения случайной составляющей профилограммы имеем

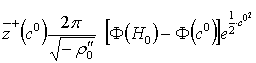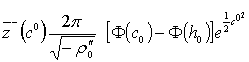, . (31)

Заметим, что в соответствии с (31)

,

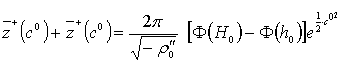т. е. на основании (21) можно написать:

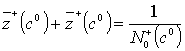, (32)

что прямо свидетельствует о справедливости всех предыдущих вычислений.

Для анализа (31) переместим начало отсчета в точки с=Н и примем, что Н=–h. Тогда

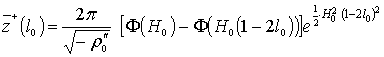
(33)

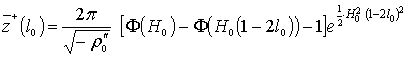
При l₀=1/2 получаем средний размер выступа и среднее расстояние между выступами профилограммы на нулевом уровне с = 0:

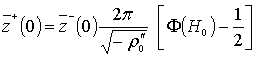. (34)

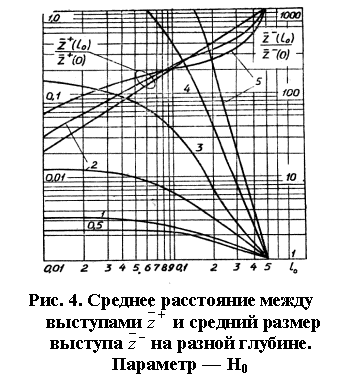
Относительный размер выступа и относительное среднее расстояние между выступами определяется равенствам (рис. 4):

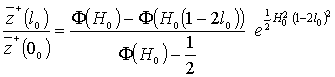
(35)

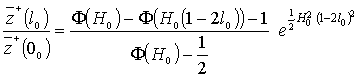
Литература

1. Евсеев Д.Г., Сальников А.Н. Физические основы процесса шлифования. Изд-во Сарат. ун-та, 1978. – 128 с.

2. Хусу А.П., Витенберг Ю.Р., Пальмов В.А. Шероховатость поверхностей. – М.: Наука, 1975. – 344 с.

3. Тихонов В.И. Выбросы случайных процессов. – М.: Наука, 1970. – 392 с.