Вялов А. С. Мицкевич В.М. Шпургалова М.Ю. Алехнович Г.Н.

Белорусский национальный технический университет

Исследование зависимости нагрузок на стены от типа крыши

Пожалуй, большинство из нас задумывались: какой же тип крыши передаст на стены меньшие усилия. В данной статье мы рассмотрели три основных типа крыши: двухскатная, плоская, односкатная. Двускатная крыша представляет собой две расположенные под углом друг к другу поверхности, опирающиеся на находящиеся на одной и той же высоте несущие стены. Плоские крыши имеют обычно небольшой уклон, чтобы с кровли эффективно скатывалась вода. Плоскими обычно называют кровли с уклоном до 3 %.

Рис.1 Двускатная крыша Рис.2 Плоская крыша

Что представляет собой односкатная крыша? Ее несущие конструкции опираются на разноуровневые наружные стены.

Рис. 3 Односкатная крыша

Вывод основных расчетных соотношений

Для простоты вычислений будем использовать вертикальную равномерно распределенную нагрузку. При этом будем учитывать, что сила, которой можно заменить нагрузку, вычисляется для треугольной нагрузки по формуле: Q=Lq, где 0≤q≤6 кН/м; для нагрузки в форме прямоугольника- Q=Lq, где q=3 кН/м, где L-длина, на которую действует нагрузка. Примем длину пролета равной 6м. Так же отметим, что Q-сила, эквивалентная нагрузке, для треугольника приложена к поверхности на расстоянии L от максимального значения интенсивности равномерно распределенной нагрузки – q . Для прямоугольной нагрузки эквивалентная сила приложена к середине поверхности.

Пусть:

-сумма проекций всех сил на ось Х;

- сумма проекций всех сил на ось Y;

-сумма моментов сил относительно точки В,

где Y-реакция опоры, возникающая в шарнирно-подвижной опоре;
Х- горизонтальная реакция опоры, возникающая в шарнирно-неподвижной опоре;

Y-вертикальная реакция опоры, возникающая в шарнирно-неподвижной опоре;

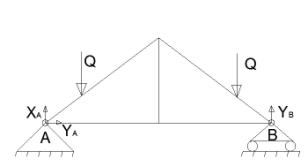1.Расчет нагрузок для двускатной крыши(α=45)

Запишем уравнения равновесия для данной системы:

=0; Х=0; (1.1)

=0; Y+ Y-2Q=0; (1.2)

=0; 6Y-Q-5Q=0. (1.3)

Так как длина пролета 6м и α=45, значит: Рис.4 упрощенная схема двускатной крышей

L=6cosα=6*=3м=>Q=*3*6=9кН.

Из (1.3) следует, что: Y=Q=9кН≈12.7 кН. Подставляя полученные данные в (1.2), получаем: Y=Q=9кН≈12.7 кН

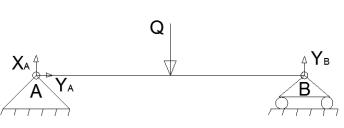
2.Расчет нагрузок плоской крыши

Для данной крыши Q=Lq=6*3=18 кН/м.

Запишем уравнения равновесия:

=0; Х=0; (2.1)

=0; Y+ Y-Q=0; (2.2)

=0; 6Y-3Q=0. (2.3) Р ис.5 упрощенная схема Плоской крыши

Из (2.3) следует, что: Y=Q=*18=9 кН. Подставляя полученные данные в (2.2), получаем: Y= Y=Q=*18=9 кН.

3.Расчет нагрузок односкатной крыши

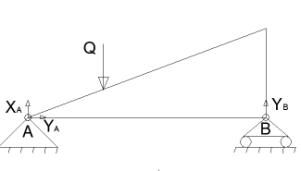Так как длина пролета 6м и α=45, значит:

L=6м.=>Q=6**6=18 кН.

Запишем уравнения равновесия:

=0; Х=0; (3.1)

=0; Y+ Y-Q=0; (3.2) Рис.6 Урощенная схема односкатной крыши

=0; 6Y-4Q=0. (3.3)

Из (3.3) следует, что: Y=Q=*18≈16,97 кН. Подставляя полученные данные в (3.2), получаем: Y=Q=*18≈8,48 кН.

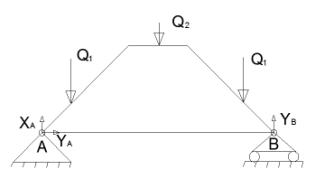
4.Расчет нагрузок трапециевидной крыши

Длина наклонных балок L=1,5м. Длина прямой части системы l=3 м. Отсюда следует, что: Q=*1,5*6=4,5кН; Q=3*3=9 кН.

Запишем уравнения равновесия:

=0; Х=0; (4.1)

=0; Y+ Y- Q- Q- Q=0; (4.2)

=0; 6Y-0,75 Q-3 Q-5,25 Q=0. (4.3)

Из (4.3) следует, что: Y= Q+ Q=

=*9+4,5≈10,86 кН. Рис.7Упрощенная схема трапециевидной крыши

Подставляя полученные данные в (4.2),

получаем: Y= Q+ Q=*9+4,5≈10,86 кН.

Вывод:

В ходе вычислений мы пришли к выводу, что при плоской крыше величины нагрузок на стены находятся в минимальном диапазоне. Но при выборе типа крыши необходимо учитывать и то, для каких целей она будет использоваться. Например, на плоской крыше можно создать сад, в скатных крышах можно задействовать чердачное помещение. Не нужно забывать, что каждый тип крыши имеет как свои преимущества (например, для двускатной: эффективное отведение снега и воды с кровли; для плоской: значительно меньшая площадь по сравнению со скатными, что помогает сэкономить материалы), так и недостатки. Например, на плоской крыше может скапливаться вода на поверхности и могут происходить протечки, а двускатная крыша имеет значительный вес конструкции и требует большее количество материала. Так же необходимо учитывать и погодные условия в регионе, и архитектурную особенность местности. Поэтому в дальнейших работах предполагается исследование и уточнение данных параметров, оказывающих влияние на величину нагрузок.