Механика

Танирбергенова А.А.

Карагандинский государственный технический университет, Казахстан

Вероятностные методы расчета

конструкций на устойчивость

Проектируемая инженером конструкция отличается от реальной многочисленными более или менее мелкими отклонениями, дефектами, несовершенствами. Инженеру необходима уверенность в том, что несмотря на наличие этих отклонений, реальная конструкция будет работать примерно также, как и соответствующая ей идеализированная конструкция. Для этого равновесие идеализированной конструкции должно обладать устойчивостью по отношению ко всем классам возмущений, отличающих её от реальной конструкции. В этом смысле условия устойчивости более органически связаны с выбором расчётной схемы, чем условия прочности и жёсткости. Так, если схема уточняется путём учёта ряда факторов, отличающих идеализированную конструкцию от реальной, то некоторые условия устойчивости могут видоизмениться или отпасть вообще. Допустим, что в качестве расчётной схемы взят идеально прямой центрально нагруженный и однородный стержень. Наиболее важными классами возмущений, отличающих реальный стержень от расчётной схемы, являются начальное искривление оси и эксцентриситет сжимающей силы. Прямолинейная форма стержня (идеализированная схема реального стержня) устойчива по отношению к этим двум классам возмущений, если сжимающая сила меньше критической. Напротив, при даже сколь угодно малые возмущения приводят к конечным прогибам.

Представим себе теперь, что величина начального прогиба и эксцентриситета заданы и расчёт ведётся по схеме искривлённого и внецентренно нагруженного стержня. В такой постановке вопрос об устойчивости прямолинейной формы по отношению к этим возмущениям снимается и заменяется отысканием напряжённо - деформированного стержня по уточнённой расчётной схеме.

Возмущения, имеющие место в реальных конструкциях, чаще всего, носят случайный характер и подчиняются некоторым статистическим закономерностям, для изучения которых необходимо накапливать опытный материал. Ввиду этого поведение конструкций при наличии возмущений должно исследоваться методами теории вероятностей и математической статистики.

Обычно возмущённое состояние описывается прогибом , а причины, вызывающие отклонения от невозмущённого состояния, - конечным числом случайных факторов с параметрами и случайными нагрузками . Случайные величины, характеризующие механические свойства материала могут быть включены в класс возмущений или в класс нагрузок. Из решения детерминистической задачи считается известной связь между этими параметрами

.

Предполагается, что известна совместная плотность вероятности возмущений

.

Задача состоит в нахождении закона распределения прогиба по заданному закону распределения возмущающих факторов. Для этого уравнение

решается относительно одного из параметров, например,

.

Эта зависимость должна быть однозначной. Дальнейшее решение задачи состоит в преобразовании плотности вероятностей по формуле типа

.

При расчёте конструкции на устойчивость часто возникает задача оценки меры опасности данного напряжённо- деформированного состояния. Эта задача принципиально не отличается от аналогичной задачи в расчётах по предельному состоянию.

Допустим, что безопасное состояние имеет место, если выполняется условие . Тогда для вероятности безопасного состояния получаем формулу

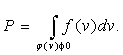
Для простейшей задачи, когда возмущения характеризуются одним параметром , а нагрузка задана одним параметром и безопасное состояние описывается условием , вероятность безопасного состояния равна

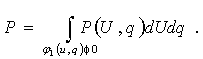
Для идеализированного стержня последняя формула позволяет найти вероятность сохранения прямолинейной формы равновесия

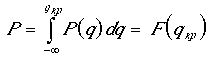
мгде – функция распределения случайной нагрузки.

С определением вероятности безопасного состояния тесно связана задача проектирования конструкции заданной надёжности.

Литература:

Бакиров Ж.Б. Вероятностные методы расчета элементов конструкций. – Караганда: КарГТУ, 2001. - 180с.