Суходоева А.А.,  Суходоев С.С.

 

Проблема потери устойчивости стержня

за пределами упругости

Аннотация

Рассматривается задача о напряженно-деформированном состоянии центрально сжатого стержня, потеря устойчивости которого происходит в пластической области. Определение критической силы и перемещений осуществляется по касательному модулю упругости методом Энгессера-Шенли.

 

Как известно из курса сопротивления материалов [1], исследование устойчивости зависит от гибкости стержня.  Вопрос потери устойчивости в упругой области длинных и тонких стержней, гибкость которых велика, был подробно рассмотрен в работе [3]. Там для определения формы изогнутой оси стержня и перемещений после потери устойчивости в упругой зоне были использованы уравнения эластики Эйлера.

Для  стержней, потеря устойчивости которых происходит в пластической области,  а это как правило стержни малой гибкости , определение критической силы и перемещений можно осуществляется по касательному модулю упругости методом Энгессера-Шенли.

В работе исследуется поведение стальных стержней разной гибкости  трубчатого сечения, шарнирно закрепленных по концам,  расчетная схема представлена на рис.1.

 

                                     

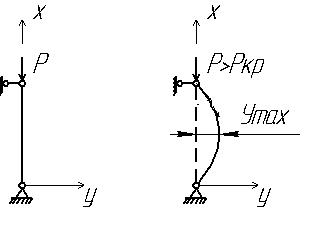
Рисунок 1. Расчетная схема
 
        

Для таких стержней потеря устойчивости происходит при напряжениях, превосходящих предел пропорциональности, т.е. в пластической области. В работе были рассмотрены два  таких стержня, размеры которых приведены в таблице 1.

Таблица 1

Размеры стержней

стержни

внутренний радиус rвн, м

наружный радиус rн, м

длина l, м

гибкость,  

3

0,0757

0,083

3,0

53

4

0,0961

0,1045

3,28

46

 

Проследим поведение стержня при возрастании сжимающей силы. Предположим, что достигнув критического значения Р0 (по формуле Энгессера-Шенли сила ), при некоторых малых возмущениях стержень изогнулся. Введем в рассмотрение изменение напряжения

                         ,                                                                (1)

где  - касательный модуль.

Так как сжимающая сила при потере устойчивости остается неизменной по предположению, то в одной части сечения будет  , в этом случае  двигаемся по диаграмме вверх (рис.2), в другой, где    происходит разгрузка, и зависимость между приращением напряжения и деформации изображается прямой, параллельной начальному, упругому участку диаграммы:

                                                                                                (2)

 

 

 

 

 

 

 

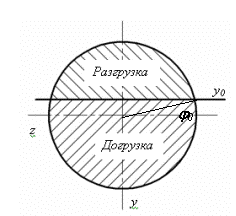
Рис.2.  Диаграмма сжатия                             Рис.3. Положение нейтральной оси

Так как сжимающая сила при потере устойчивости остается постоянной, то

                                                  

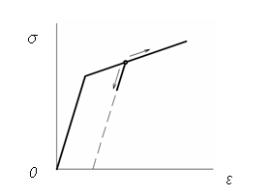
Ось у0  делит сечение на две части, в одной справедливо соотношение (1), в другой – соотношение (2), причем положение этой нейтральной оси заранее неизвестно (рис.3).

Будем считать материал следующим диаграмме сжатия с линейным упрочнением, т.е. касательный модуль постоянный Ет =0,5 ×105  МПа [ 2]. Обозначим De – изменение оси стержня при изменении силы от Р0  до Р,

 

c – соответствующую кривизну изогнутой оси. Дефрмацию волокна с координатой  у обозначим

На нейтральной оси она равна нулю, следовательно,

.

Таким образом, уравнения (1) и (2) примут вид:

 

Вычислим  приращение силы и изгибающий момент

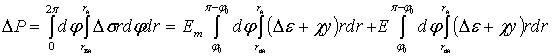      ( 3)     

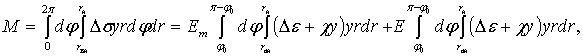
где можно выразить

Определим  поперечные перемещения сжатого стержня, если учтем, что момент в сечении с координатой x равен  , а кривизна изогнутой оси

 

 

Окончательно, дифференциальное уравнение примет вид

а с учетом формулы Энгессера-Шенли

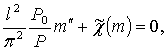
где ,      - безразмерные величины, полученные из выражений (3).

В таблице 4 приведены значения критической силы, вычисленной по касательному модулю для двух стержней и значения вертикального перемещения конца стержня и максимальный прогиб при s=l/2. Так как критическая сила для стержней малой гибкости существенно больше, чем у гибких стержней, то и перемещения, особенно продольные, также больше, а вот поперечные перемещения отличаются незначительно.

Таблица 2

Результаты расчетов

 

Р0, МН

Xmax, мм

Y max, мм

1

0,63

10

39,1

2

1,22

15

40,2

 

 

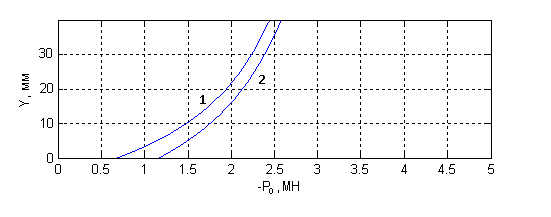Рис.4. Зависимость величины поперечного перемещения сечения

s=l/2 в 1 и 2 стержнях.

На рисунке 4 показано изменение поперечного перемещения от приложенной продольной силы. Видно, что при Р=Р0  прогиб первоначально прямого стержня равен нулю, а затем резко возрастает. Фактически за момент потери устойчивости принимается момент, когда прогиб достигает некоторой достаточно большой величины, но значения силы при этом настолько большие, что напряжения превосходят предельные значения. Таким образом,  негибкие стержни можно рассчитывать только на прочность.

 

Список литературы

1.                             Горшков А.Г., Трошин В.Н., Шалашилин В.И.  Сопротивление материалов: Учеб. пособие – М.: ФИЗМАТЛИТ, 2008. – 544 с.

2.                             Третьяков А.В., Зюзин В.И. Механические свойства металлов и сплавов при обработке давлением. Справочник. – М: Металлургия, 1973. – 224с.

3.                             Работнов Ю.Н. Механика деформируемого твердого тела. – М: Наука, 1988. – 712 с.