Математика/ 3. Теория вероятностей и математическая статистика

к.ф.-м.н. Искакова А.С., Сеилханов А.С., Дюсембаева Р.Т.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Школа-лицей №1 города Астаны, Казахстан

Построение вероятностной модели событий зависимых от факторов

Многомерные вероятностные модели, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни. В последние годы было разработано значительное количество вероятностных моделей. Тем не менее остается много не решенных проблем, когда пронаблюдать возможно только суммы компонентов, которые в результате наблюдений невозможно выявить. До настоящего времени вероятностные модели, описывающие подобные ситуации, не рассматривались. Исключительным актуальным примером применения подобной модели является рекламная индустрия, когда необходимо увязать распределение потребительских интересов с соответствующей рекламой в различных источниках. Аналогичные проблемы очень часто встречаются в метеорологии и в других областях. В этой работе представляются статистические оценки распределения сумм случайных значений L₁, … , L_d, когда L₁, … , L_d не наблюдаемы, а наблюдаемы только их суммы. Тем самым результаты предложенной работы позволяют решить многие из вышеперечисленных проблем.

Предположим, что на некоторое событие x влияет N факторов с некоторой степенью действия. Определим каждый фактор одним из возможных чисел l₁, l₂, ..., l_n. Пусть значения p₁, … , p_n определяют влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие x, и

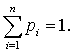
Пример 1. Пусть на событие х могут влиять факторы 1, 2 и 3. Если фактор 1 влияет с вероятностью 0,3, фактор 2 – с вероятностью 0,5, тогда фактор 3 – вероятностью равного 1-0,3-0,5=0,2.Рассмотрим случай, когда на событие х могут влиять k факторов с повторениями. Причем фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз. Очевидно, что

.

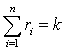Теорема 1. Количество всевозможных влияний k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз, есть

.

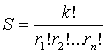Доказательство. Количество всевозможных k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз есть полиномиальный коэффициент

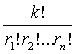
(см [1] стр.12).

Теорема доказана.

Теорема 2. Вероятность того, что на событие х повлияли k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз, есть

,

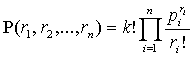где значения p₁, … , p_n определяют вероятности (или частности) влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие х.

Доказательство. Вероятность того, что на событие х повлияли k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз, есть полиномиальная вероятность (см [2] стр.84), которая представляется как

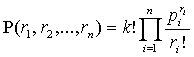. (1)

Теорема доказана.

Пример 2. Пусть на событие х могут влиять факторы 1, 2 и 3. Фактор 1 влияет с вероятностью 0,3, фактор 2 – с вероятностью 0,5 и тогда фактор 3 – вероятностью 0,2. На событие х повлияли 5 факторов. Определим вероятность, что на событие повлияли 1 раз фактор и 4 раза фактор 2.

Решение. Из примера 1 имеем, Подставим эти значения в формулу (1) при k=5, и получаем

.

Ответ: .

Литература:

1. Дж. Риодан. Введение в комбинаторный анализ. Перевод с англ. Л.Е. Садовского. М.: изд. Ин. лит. 1963 г. 287 с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва: Юнити. 2006 г., 571 с.

3. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

4. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

5. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

6. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.

1