Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Попова Н.В.

ФГБОУ ВПО «РЭУ им. Г.В. Плеханова», Россия

О применении математических методов в финансовом анализе

Как известно, начиная примерно с середины ХХ в. математические методы активно применяются в теории финансовых инвестиций. Теория финансовых инвестиций с фиксированным доходом в условиях определенности является основой современной теории финансовых инвестиций, что подтверждается в специальном исследовании [1]. Основной объект изучения этой теории - безрисковые ценные бумаги (облигации). В связи с особой ролью таких бумаг на фондовом рынке, развитие этой теории представляет и практический интерес. К настоящему времени в теории рассмотрены основные инвестиционные свойства облигации. Получены их математические доказательства. В работах [2, 3] приводятся доказательства влияния основных факторов – доходности, купонной ставки и срока до погашения на цену, показатели дюрации и выпуклости облигации, а также портфеля облигаций. Таким образом, применение математических методов способствует формированию и развитию теории.

Есть еще одна сторона таких исследований. В ходе решения задачи об инвестиционном свойстве облигации приходится решать определенную математическую задачу, что иногда вынуждает автора проводить дополнительные исследования. В результате решения таких специальных задач могут появиться новые результаты.

Например, в работе [4] рассмотрена задача о влиянии частоты купонных выплат на цену облигации, где котируемая цена облигации рассматривается как функция числа купонных платежей в году: . Здесь − функция, определенная на множестве , а , , , – фиксированные параметры облигации. Для решения задачи потребовалось воспользоваться свойствами функции на множестве . Известно, что . Монотонность этой функции установлена для целочисленного положительного аргумента в теории числовых последовательностей. Более подробно свойства этой функции в литературе не упоминаются. В связи с этим были доказаны следующие утверждения о функции [5]:

1) функция является возрастающей и вогнутой на множестве ;

2) абсолютное изменение функции при увеличении на 1 тем больше, чем меньше , т.е. , где ;

3) относительное изменение функции при увеличении на 1 тем больше, чем меньше , т.е. , где .

Доказательства этих утверждений получены с помощью разложений функций в степенные ряды, теорем о дифференцируемых функциях и теорем выпуклого анализа. Решение этой вспомогательной задачи само по себе представляет интерес и дополняет теорию функций. На основании доказанных свойств функции в работе [4] установлена ранее не изученная зависимость цены купонной облигации от числа купонных платежей в году. Например, одна из теорем и ее доказательство имеют вид.

Теорема. При фиксированных значениях , и , где , относительное изменение котируемой цены облигации при изменении числа купонных платежей в году на 1 тем больше, чем меньше число купонных платежей в году:

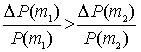, где .

Действительно, пусть (облигация продаётся с дисконтом). Так как

,

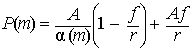то

,

,

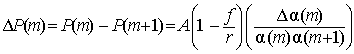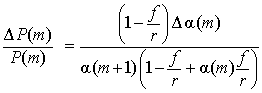где . Тогда отношение

,

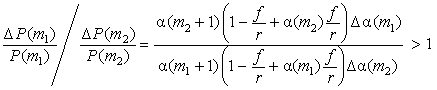поскольку , , при . Для облигации, продающейся с премией , доказательство базируется на теоремах, доказанных в [4]. Приведенные в работе [4] конкретные вычисления подтверждают справедливость доказанных теорем.

Другой пример вспомогательной задачи. В работе [6] доказана теорема о влиянии срока до погашения на изменчивость цены облигации. Решение основной задачи и в этом случае потребовало решения вспомогательной задачи в виде доказательства специальной теоремы. Чтобы установить влияние уровня доходности рынка на абсолютное и относительное изменение цены облигации при изменении ее срока до погашения на один купонный период, была доказана следующая теорема.

Теорема. При фиксированном справедливы следующие утверждения:

1) и являются убывающими функциями на отрезке

(облигация продается с премией при и по номиналу при );

2) существуют точки максимумов функции и функции на

множестве (облигация продается с дисконтом при ).

Абсолютное и относительное изменения цены облигации при уменьшении срока до погашения на один купонный период рассматриваются как функции доходности . Эта теорема является естественным продолжением одной из рыночных теорем. Однако ранее эта зависимость не изучалась. Для доказательства теоремы использованы достаточные условия монотонности и глобального экстремума дифференцируемой функции.

Результаты доказанной теоремы оказались необходимы при доказательстве зависимости изменчивости цены облигации от срока до погашения. Например, доказательство утверждения теоремы о поведении последовательности абсолютных изменений цены облигации, продающейся с премией, при увеличении ее доходности на имеет вид. Сравним -й и -й члены последовательности. Рассмотрим разность:

.

Значит, последовательность является возрастающей. Здесь и − абсолютные изменения цены облигации при уменьшении срока до погашения на один купонный период при уровнях доходности и соответственно, рассмотренные в приведенной теореме. Согласно утверждению 1, . Как видим, решение основной задачи потребовало решения вспомогательной задачи в виде доказательства приведенной теоремы. Таким образом, работа [6] является примером того, что применение математических методов позволяет установить новые инвестиционные свойства облигации, которые в условиях реального рынка могут явно не проявляться, однако оказывают влияние на известные инвестиционные свойства.

Рассмотрены некоторые задачи в теории финансовых инвестиций с фиксированным доходом. Как видим, применение математических методов не только способствует развитию этой теории, но и порождает новые задачи, в результате чего могут появиться новые результаты в теории функций или теории инвестирования.

ЛИТЕРАТУРА

1. Geoffrey Poitras Frederick R. Macaulay, Frank M. Redington and the Emergence of Modern Fixed Income Analysis. - 2006 – Citeseer.

2. Барбаумов В. Е., Гладких И. М., Чуйко А. С. Финансовые инвестиции с фиксированным доходом (количественный анализ): Учебное пособие. – М.: Изд-во РЭА им. Г.В.Плеханова, 2006. - 112 с..

3. Мельников А. В., Попова Н. В., Скорнякова В. С. Математические методы финансового анализа. – М.: Анкил, 2006.

4. Попова Н.В. Влияние частоты купонных платежей на цену облигации // Вестник финансового университета. – 2012. – № 3 (69).

5. Попова Н.В. Показательно-степенная функция в задаче о цене облигации. Материалы VIII международной научно-практической конференции «Теория и практика современной науки». 2012 г. Москва: Институт стратегических исследований.

6. Попова Н.В. Влияние срока до погашения на изменчивость цены облигации // Вестник финансового университета. – 2013. – № 3(75).