А. А. Кудь, А. Б. Щукин, А. В. Макаричев, д.ф.- м.н., доц.

Национальный аэрокосмический университет «ХАИ»

Харьковский национальный автомобильно-дорожный университет

Московский государственный университет им. М.В. Ломоносова

ОБСЛУЖИВАНИЕ БЕЗ ОЖИДАНИЯ СЛУЧАЙНЫХ ПРИРАЩЕНИЙ ГРУППОВЫХ ПОСТУПЛЕНИЙ СУММ

В систему массового обслуживания поступает входящий поток групп требований , . Число требований в группе представляет собой случайную величину с натуральными значениями:

, ,

и производящей функцией

.

С каждой такой -й группой () из требований связана случайная сумма

независимых в совокупности одинаково распределенных случайных слагаемых с функцией распределения и характеристической функцией

.

Характеристическая функция суммы случайных приращений

имеет вид

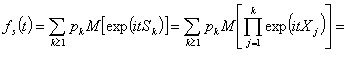
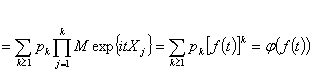
В системе массового обслуживания группы требований обслуживаются без ожидания. Времена обслуживания групп требований неотрицательны и независимы в совокупности. Обозначим функцию распределения времени обслуживания группы требований (суммы слагаемых).

Предположим, что в начальный момент времени в системе массового обслуживания нет требований. Обозначим число групп требований (сумм слагаемых), поступивших в систему обслуживания на отрезке времени , число обслуженных групп требований (сумм слагаемых) в системе массового обслуживания на отрезке времени , а число групп требований (сумм слагаемых), находящихся на обслуживании в системе в момент времени . Очевидно

.

Распределение числа пришедших групп требований (сумм слагаемых) в систему на отрезке времени определяется по формуле [1]

,

где .

Обозначим

характеристическую функцию для суммы

всех сумм всех групп приращений сумм, обслуженных на отрезке .

Обозначим

интеграл от интенсивности пуассоновского потока с переменным параметром

,

для числа поступивших на отрезке групп требований (сумм слагаемых) и обслуженных на нем. Тогда характеристическая функция для суммы

всех сумм всех групп приращений сумм, обслуженных на отрезке , имеет вид

.

Дифференцированием ее в нуле находим математическое ожидание для суммы

всех сумм всех групп приращений сумм, обслуженных на отрезке ,

,

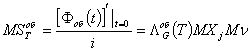второй момент этой случайной величины

,

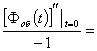
и ее дисперсию

.

Обозначим характеристическую функцию для суммы

всех сумм всех групп приращений сумм, находящихся на обслуживании в момент времени . Обозначим

интеграл от интенсивности пуассоновского потока с переменным параметром

,

для числа поступивших на отрезке групп требований (сумм слагаемых) и продолжающих свое обслуживание в момент времени , то есть не закончившим обслуживание на нем. Тогда характеристическая функция для суммы

всех сумм всех групп приращений сумм, поступивших, но не обслуженных на отрезке , имеет вид

.

Дифференцированием ее в нуле находим математическое ожидание для суммы

всех сумм всех групп приращений сумм, обслуженных на отрезке ,

,

второй момент этой случайной величины

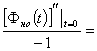
и ее дисперсию

.

Литература.

1. Хинчин А. Я., Работы по математической теории массового обслуживания, Физматгиз, Москва, 1963, 236 с.

2. B. V. GNEDENKO AND I. N. KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

3. Климов Г. П. Стохастические системы обслуживания, М., 1966, 244 стр. с илл.

4. Соловьев А. Д. Асимптотическое поведение момента

наступления редкого события в регенерирующем процессе.

Известия АН СССР. Техническая кибернетика, 1971, № 6, с.

79-89.

5. Вопросы математической теории надежности /Е.Ю.

Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,

А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:

Радио и связь, 1983.- 376 с., ил.

6. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.