Математика/ 3. Теория вероятностей и математическая статистика

к.ф.-м.н Искакова А.С., Сеилханов А.С., Дюсембаева Р.Т.

Евразийский национальный университет имени Л.Н. Гумилева

Школа-лицей №1 города Астаны, Казахстан

Вероятностное распределение суммы факторов влияющих на событие

Предположим, что на некоторое событие x влияет N факторов с некоторой степенью действия. Определим каждый фактор одним из возможных чисел

l₁, l₂, ..., l_n.

Пусть значения

p₁, … , p_n

определяют влияния фактора с соответствующим числом

l₁, l₂, ..., l_n

на событие x, и

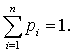
Пусть значение u представляет сумму чисел на k факторов повлияющих на событие х. То есть

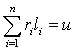. (1)

Последняя формулая явлется формулой разбиения числа u на части

l₁, l₂, ..., l_n

числом разбиений n.

Рассмотрим всевозможные значения сумм k чисел из возможных вынутых из урны шаров.

Пример 1. На событие х могут повлиять факторы 5, 7, 11. На событие х повлияли 3 фактора. Тогда всевозможные суммы влияний факторов на событие х есть

,

,

,

,

,

,

,

,

..

Теорема. Вероятность того, что сумма чисел на k повлияющих факторах с повторениями на событие x равна u, определяется по формуле

.

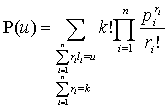Доказательство. Разумеется, что, если имеет место разбиения u на l₁,…, l_d, то система уравнений

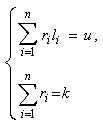
имеет один или более решений. Вероятность каждого разбиения u на l₁,…, l_d, определяется теоремой 3. Таким образом, пришли к доказательству теоремы.

Теорема доказана.

Пример 2. На событие х могут повлиять факторы 1, 2, 4. Фактор 1 влияет на событие х с вероятностью 0,2, фактор 2 – с вероятностью 0,5 и фактор 4 – с вероятностью 0,3. На событие х повлияли 3 фактора. Определим вероятность, что сумма факторов влияющих на событие х примет значение 6.

Решение. Из условия задачи k=3. Сумма чисел на факторах повлияющих на событие х может принять значение 6, когда будут влиять два фактора с числом 1 и один фактор с числом 4 или три фактора с числом 2.

То есть u=6, если

или

.

Тогда по теореме имеем

.

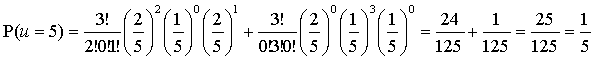Литература

1. Дж. Риодан. Введение в комбинаторный анализ. Перевод с англ. Л.Е. Садовского. М.: изд. Ин. лит. 1963 г. 287 с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва: Юнити. 2006 г., 571 с.

3. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

4. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

5. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

6. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84