Математика/ 3. Теория вероятностей и математическая статистика

к.ф.-м.н Искакова А.С., Сеилханов А.С., Дюсембаева Р.Т.

Евразийский национальный университет имени Л.Н. Гумилева

Школа-лицей №1 города Астаны, Казахстан

Оценивание параметров распределения одного многмерно дискретного распределения вероятностей

Предположим, что на некоторое событие x влияет N факторов с некоторой степенью действия. Определим каждый фактор одним из возможных чисел l₁, l₂, ..., l_n. Пусть значения p₁, … , p_n определяют влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие x, и

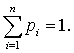
Вероятность того, что на событие х повлияли k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз, есть

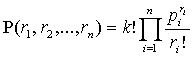, (1)

где значения p₁, … , p_n определяют вероятности (или частности) влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие х

Пусть значение u представляет сумму чисел на k факторов повлияющих на событие х. Рассмотрим всевозможные значения сумм k чисел из возможных вынутых из урны шаров.

Вероятность того, что сумма чисел на k повлияющих факторах с повторениями на событие x равна u, определяется по формуле

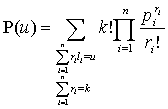. (2)

Очевидно, что на практике не известны элементы вектора p=(p₁, …, p_n).

Следовательно, формулы (1) и (2) не находят фактического применения. В связи с этим возникает необходимость определения оценки вероятностей (1) и (2).

Как известно, из курса теории вероятностей и математической статистики, хорошим приближением к вероятностям p₁, …, p_n служат статистические оценки, полученные из ряда фактических данных.

Допустим, имеем m сумм u₁, ..., u _m k факторов влияющих на событие х, то есть u_i, i=1 ,..., m, i –ая сумма k факторов влияющих на событие х.

Для каждого i=1, ..., m определим V_i число разбиений u_i на числа l₁, … , l_m.

Векторы

r_1i=(r_11i,…, r_n1i),

…

r_Vi=(r_1Vi,…, r_nVi),

определяющие эти разбиения, при v_i=1,..., V_i, являются решениями следующей системы уравнений

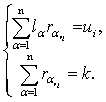(3)

Пусть для каждого j=1,…, μ, где

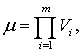
существует вектор

z_j=(z_1j,..., z_dj),

определяемый как

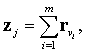(4)

причем индексы в правой и левой части связаны между собой взаимно однозначным соответствием, которое не единственно. Например, это соответствие можно описать следующим способом

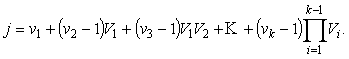(5)

Также его можно представить как

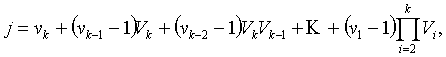
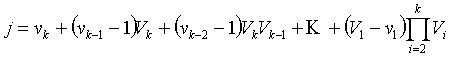
или другими способами

Следующая лемма позволяет определить, какие именно векторы

r_v1, r_v2,…, r_vm

при v₁=1,…, V₁, …, v_k=1,…, V_k в сумме образовали вектор z_j=(z_1j,..., z_dj). Пусть для любого действительного a значениеопределяет целую часть числа a.

Лемма. Если индексы в правой и левой частях уравнения (4) связаны между собой соответствием (5), то

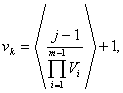
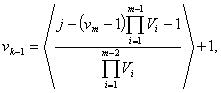
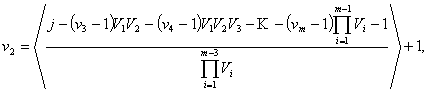
Доказательство. Из (5) следует, что

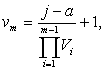
где Очевидно, что последнее можно представить в следующем виде

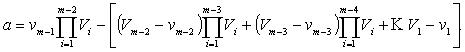
Так как

то или 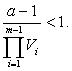Так как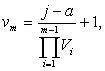

то

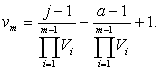
Ввиду того, что

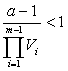
и v_m – неотрицательное целое число, то

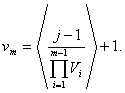
Аналогично тому, как была определена v_k в последней формуле, определяются v_m-1, v_k-2, …, v₁, принимающие следующие значения

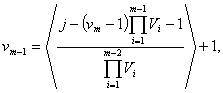
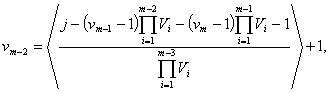
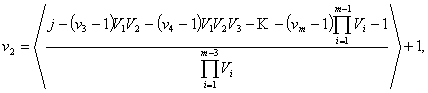
Лемма доказана.

Теорема. Элементы множества

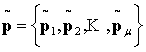
являются оценками для параметров

p=(p₁,…, p_n)

распределения (2), которые при j=1, …, μ определяются как

где m≥1.

Литература

1. Дж. Риодан. Введение в комбинаторный анализ. Перевод с англ. Л.Е. Садовского. М.: изд. Ин. лит. 1963 г. 287 с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва: Юнити. 2006 г., 571 с.

3. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

4. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

5. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84