Математика/ 3. Теория вероятностей и математическая статистика

к.ф.-м.н Искакова А.С., Сеилханов А.С., Дюсембаева Р.Т.

Евразийский национальный университет имени Л.Н. Гумилева

Школа-лицей №1 города Астаны, Казахстан

Наиболее подходящие оценки параметров одного дискретного распределения вероятностей

Предположим, что на некоторое событие x влияет N факторов с некоторой степенью действия. Определим каждый фактор одним из возможных чисел l₁, l₂, ..., l_n. Пусть значения p₁, … , p_n определяют влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие x, и

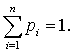
Вероятность того, что на событие х повлияли k факторов с повторениями, при которых фактор l₁ повлиял на событие х r₁ раз, фактор l₂ повлиял на событие х r₂ раз и так далее фактор l_n повлиял на событие х r_n раз, есть

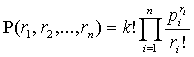, (1)

где значения p₁, … , p_n определяют вероятности (или частности) влияния фактора с соответствующим числом l₁, l₂, ..., l_n на событие х

Пусть значение u представляет сумму чисел на k факторов повлияющих на событие х. Рассмотрим всевозможные значения сумм k чисел из возможных вынутых из урны шаров.

Вероятность того, что сумма чисел на k повлияющих факторах с повторениями на событие x равна u, определяется по формуле

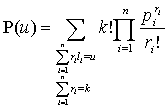. (2)

Очевидно, что на практике не известны элементы вектора p=(p₁, …, p_n).

Следовательно, формулы (1) и (2) не находят фактического применения. В связи с этим возникает необходимость определения оценки вероятностей.

Как известно, из курса теории вероятностей и математической статистики, хорошим приближением к вероятностям p₁, …, p_n служат статистические оценки, полученные из ряда фактических данных.

Допустим, имеем m сумм u₁, ..., u _m k факторов влияющих на событие х, то есть u_i, i=1 ,..., m, i –ая сумма k факторов влияющих на событие х.

Для каждого i=1, ..., m определим V_i число разбиений u_i на числа l₁, … , l_m.

Векторы r_1i=(r_11i,…, r_n1i), …, r_Vi=(r_1Vi,…, r_nVi), определяющие эти разбиения, при v_i=1,..., V_i, являются решениями следующей системы уравнений

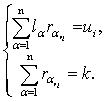(3)

Пусть для каждого j=1,…, μ, где 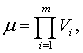существует вектор z_j=(z_1j,..., z_dj), определяемый как

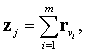(4)

причем индексы в правой и левой части связаны между собой взаимно однозначным соответствием, которое не единственно.

Теорема. Элементы множества

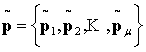
являются оценками для параметров

p=(p₁,…, p_n)

распределения (2), которые при j=1, …, μ определяются как

где m≥1.

Рассмотрим задачу определения наиболее подходящей оценки. Из решения системы уравнений (3) видно, что при i=1,…, m число u_i разбивается на числа l₁,…, l_n V_i³1способами. В случае, если V_i>1, то не известно, каким вариантом v_i=1, …, V_i сложений произведений чисел на соответствующих значениях r_1vi, … , r_dvi получили число u_i. В связи с этим имеем множество решений основанных на наблюдении, и множество несмещенных оценок для вероятности распределения (2)

Определение 1. Решение , основанное на наблюдении, является наиболее подходящим из множества 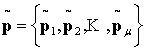, если

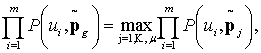(7)

где при i=1, … , k элементы множества являются оценками для вероятности P(U=u), распределения (2).

Определение 2. Оценка 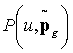для вероятности P(U=u) распределения (2) является наиболее подходящей из всего множества оценок , если – наиболее подходящее решение, основанное на наблюдении.

Пример. На событие х могут повлиять факторы 1, 2, 4. На событие х повлияли 3 фактора. Требуется определить формулу построения наиболее подходящей ценки для вероятности P(U=u) распределения (2) по имеющей реализации выборки объема m=10 u =( u ₁, ... , u₁₀), где

u ₁=3, u ₂=6, u ₃=3, u ₄=12, u ₅=10, u ₆=10, u ₇=7, u ₈=3, u ₉=7, u ₁₀=3.

Из условия задачи видно, что k=3. Решая систему уравнений (3) для каждого элемента вектора u =( u ₁, ... , u₁₀), получаем следующее

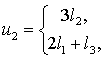
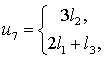
где l₁=1, l₂=2, l₃=4, определяются из условия. Следовательно, имеем

V₁=1 и r₁₁=(3, 0, 0), V₂=2 и r₁₂=(0, 3,0), r₂₂=(2, 0,1), V₃=1 и r₁₃=(3, 0, 0),

V₄=1 и r₁₄=(0, 0, 3), V₅=1 и r₁₅=(0, 1,2), V₆=1 и r₁₆=(0, 1, 2), V₇=2 и r₁₆=(0, 3, 0), r₁₆=(2, 0, 1), V₈=1 и r₁₈=(3, 0, 0), V₉=1 и r₁₉=(1, 1,1), V₁₀=1 и r₁₁₀=(3, 0, 0).

Из чего имеем

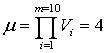
и векторы решений, основанные на наблюдении,

z₁=(13, 9,8), z₂=(15, 6,9), z₃=(15,6, 9),z₄=(17, 3,10),

получаемые с использованием (4), где элементы в правой и левой частях связаны между собой соотношением (5). При вычислении оценок для вероятности проявления элементов реализации выборки получаем с использованием полученных векторов решений, основанных на наблюдении, решение z₄, основанное на наблюдении x, является наиболее подходящим решением из всего множества решений z={z₁, z₂, z₃, z₄}.

Литература

1. Дж. Риодан. Введение в комбинаторный анализ. Перевод с англ. Л.Е. Садовского. М.: изд. Ин. лит. 1963 г. 287 с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва: Юнити. 2006 г., 571 с.

3. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

4. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

5. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84