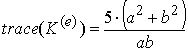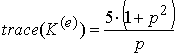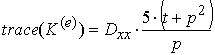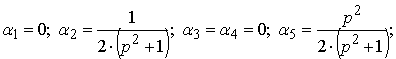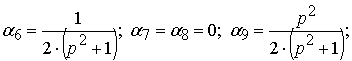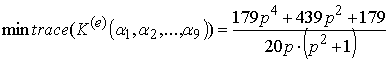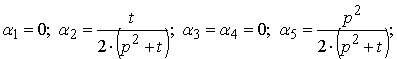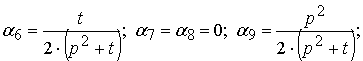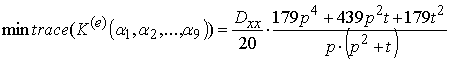Математика / 4. Прикладная математика

Безердян С.І., Старун Н.В., Білоусова Т.П., Тулученко Г.Я.

Херсонський національний технічний університет, Україна

ПРО ВПЛИВ ГЕОМЕТРИЧНОЇ ФОРМИ НА АПРОКСИМАЦІЙНІ ВЛАСТИВОСТІ ТРИКУТНИХ СКІНЧЕННИХ ЕЛЕМЕНТІВ

Постановка проблеми. Як відомо, найкращі апроксимаційні властивості мають скінченні елементи (СЕ) у формі правильних плоских фігур або просторових тіл [1]. Проте при розв’язанні практичних задач скінченноелементні сітки містять комірки як правильної, так і неправильної форми. Тому актуальними є дослідження можливостей компенсації негативного впливу неправильної форми геометричного носія на апроксимаційні властивості скінченного елемента за рахунок модифікації базисних функцій останнього.

Аналіз останніх досліджень і публікацій. Фахівці з методу СЕ не втрачають інтересу до СЕ у формі прямокутних рівнобедрених трикутників
[2-3]. Це пояснюється такими позитивними рисами вказаних елементів як можливість їх сполучення у сітках із прямокутними елементами, краща обумовленість матриць жорсткості, ніж при застосуванні різносторонніх елементів тощо. Крім того, для СЕ саме такої геометричної форми вдається побудувати базиси з додатковими властивостями в результаті розв’язання задач Діріхле методом Фур’є в областях у вигляді квадратів, які складені різними способами із прямокутних рівнобедрених трикутників [2-3].

Нами показано [4-5], що для розв’язання цих же задач доцільно використовувати матод Рітца. При цьому спрощується як сам алгоритм розвязання, так і структура отримуваних розв’язків у вигляді степеневих, а не тригонометричних поліномів. Оцінки апроксимаційних властивостей базисів, побудованих на основі методу Рітца, є ідентичними до оцінок базисів, побудованих на основі методу Фур’є.

В той же час при розв’язанні практичних задач із застосуванням обговорюваних СЕ виявлено, що їх використання може не приводити до очікуваного зростання точності отримуваних розв’язків [6-7].

Ціль публікації. Ціллю публікації є дослідження функціональних залежностей між геометричними характеристиками скінченних елементів вищих порядків у формі прямокутних трикутників і локальними характеристиками їх апроксимаційних властивостей.

Основна частина. Відмова від застосування методу Фур’є для модифікації базисів дозволяє узагальнити результати досліджень на прямокутні трикутники із катетами різної довжини. Будемо вважати, що вирази базисних функцій для всіх досліджуваних у статті елементів є відомими читачеві або їх легко знайти в усіх монографіях з методу СЕ.

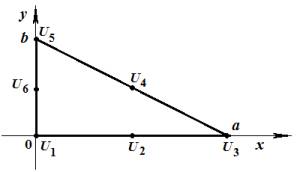
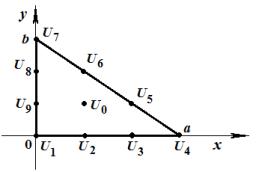
Трикутний СЕ ІІ порядку. Розглянемо трикутний СЕ ІІ порядку у формі прямокутного трикутника із катетами довжиною а і b (рис. 1).

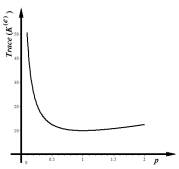
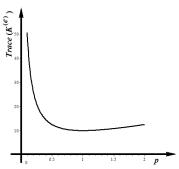
Рис. 1. Трикутний СЕ ІІ порядку у формі прямокутного трикутника	Рис. 2. Графік залежності сліду матриці жорсткості (2) від співвідношення довжин катетів р

Обчислимо для нього матрицю жорсткості, вважаючи матрицю коефіцієнтів пружності ізотропного середовища одиничною. Як відомо [1], слід матриці жорсткості є локальною характеристикою апроксимаційних властивостей застосовуваного базису. В нашому випадку маємо, що слід матриці жорсткості елемента у формі прямокутного різностороннього трикутника дорівнює:

.

(1)

Якщо покласти , то стає очевидним той факт, що величина сліду матриці жорсткості досліджуваного елемента не залежить від площі трикутника, а залежить виключно від співвідношення довжин катетів:

.

(2)

Як легко встановити, залежність (2) має мінімум , коли трикутник має катети рівної довжини (рис. 2).

Залежність (2) показує, для ортотропного середовища слід матриці жорсткості може бути зменшений за рахунок доцільного співвідношення довжин катетів використовуваного СЕ. Нехай матриця коефіцієнтів пружності середовища має вигляд 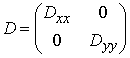, при чому . Тоді величина сліду матриці жорсткості елемента дорівнює:

(3)

і досягає мінімуму , коли .

Трикутний СЕ ІІІ порядку. Розглянемо тепер трикутний СЕ ІІІ порядку у формі прямокутного трикутника із катетами довжиною а і b (рис. 3).

Рис. 3. Трикутний СЕ ІІІ порядку у формі прямокутного трикутника	Рис. 4. Графік залежності сліду матриці жорсткості (2) від співвідношення довжин катетів р

Для СЕ із внутрішніми вузлами доцільним є застосування операції внутрішньої конденсації, що веде до зменшення розмірності глобальної матриці жорсткості.

Мають місце різні підходи до реалізації операції конденсації при розв’язанні певних класів граничних задач [8-11]. При цьому думки авторів щодо наслідків виключення внутрішніх вузлів елементів для апроксимуючих властивостей базисів різняться. У роботі [9] відзначається, що апроксимуючі властивості модифікованого елемента можуть знижуватися у порівнянні із вихідним елементом. У роботі [11] автором наводиться доведена ним теорема про обчислювальну еквівалентність базисів, які отримують у результаті операції конденсації.

Встановимо значення параметрів внутрішньої конденсації для досліджуваного СЕ, які приводять до мінімального сліду матриці жорсткості елемента:

,

(4)

де - стандартні базисні функції трикутного СЕ ІІІ порядку; - базисні функції того ж елемента після операції внутрішньої конденсації; - параметри конденсації, .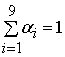

Нехай, як і раніше, між довжинами катетів існує співвідношення , тоді для задачі мінімізації сліду матриці жорсткості елемента

(4)

маємо такий розв’язок:

.

Графік функції мінімуму сліду матриці жорсткості елемента ІІІ порядку подібний до аналогічного графіку для елемента ІІ порядку (рис. 2). Найменший із можливих мінімумів досягається, коли прямокутний трикутник є рівнобедреним і .

Знову розглянемо ортотропне середовище, для якого матриця коефіцієнтів пружності має вигляд 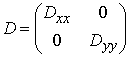, при чому . В цьому випадку задача мінімізації (4) приводить до розв’язку:

.

Аналогічно до результату з СЕ ІІ порядку найменший із мінімумів досягається, коли .

Висновки. На основі відомих загальних теоретичних закономірностей отримані у явному вигляді залежності величини сліду матриці жорсткості елемента від геометричних характеристик самого елемента та характеристик середовища для СЕ ІІ і ІІІ порядків у формі прямокутних різносторонніх трикутників. Показано, що для ізотропного середовища доцільним є використання сіток із прямокутними рівнобедреними трикутниками. Для ортотропних середовищ встановлено залежність співвідношення довжин катетів досліджуваних СЕ від співвідношення коефіцієнтів пружності середовища, яка приводить до найменшого із можливих мінімумів сліду матриці жорсткості елемента. Вказані результати дозволяють підвищувати точність розв’язків за методом СЕ при практичних розрахунках.

Література

1. Секулович М. Метод конечных элементов / М. Секулович. — М.: Стройиздат, 1993. — 664 с.

2. Юлдашев О.И. Гармонические базисные функции для конечных элементов высокого порядка аппроксимации [Электронный ресурс] / О.И. Юлдашев, М.Б. Юлдашева // ОИЯИ. Лаборатория ИТ. Научный отчет 2006-2007. — Дубна: ОИЯИ, 2007. — С. 317—320. — Режим доступа к отчету: http://lit.jinr.ru/Reports/SC_report_06-07/pdfall/p317.pdf.

3. Пашковский А.В. Численно-аналитические методы стандартных элементов для моделирования стационарных физических полей в линейных кусочно- однородных и нелинейных средах : дисс. … доктора техн. наук : 05.13.18 "Математическое моделирование, численные методы и комплексы программ" / Александр Владимирович Пашковский. — Новочеркасск, 2014. — 364 с.

4. Тулученко Г.Я. Побудова базисів трикутних скінченних елементів, які адаптовані до виду граничної задачі (повідомлення 1) / Г.Я. Тулученко, О.В. Котова, С.І. Безердян // Вісник Херсонського національного технічного університету. – 2014. – Вип. 3 (50). – С. 502–505.

5. Безердян С.І. Дослідження динаміки змін показників якості базисів скінченних елементів при їх модифікації / С.І. Безердян, Т.П. Білоусова, Г.Я. Тулученко // Матеріали Всеукраїнської науково-практичної конференції "Сучасні енергетичні установки на транспорті і технології та обладнання для їх обслуговування" (м. Херсон, 1-3 жовтня 2014 р.). – Херсон : ВНЗ "ХДМА", 2014. – С. 353—354.

6. Безердян С.І. Суперечливі оцінки апроксимаційних властивостей гармонічних базисів трикутного скінченного елемента II порядку / С.І. Безердян, Г.Я. Тулученко // Тези доповідей ІІІ Міжнародного форуму студентів, аспірантів і молодих вчених (м. Дніпропетровськ, 23-24 квітня 2015). — Дніпропетровськ: ДНУ, 2015. — С. 475—477.

7. Безердян С.І. Практична перевірка прогнозованих властивостей модифікованих базисів трикутного скінченного елемента ІІ порядку / С.І. Безердян, Т.П. Білоусова, Г.Я. Тулученко // Матеріали Міжнародної науково-методичної конференції "Сучасні науково-методичні проблеми математики у вищій школі" (м. Київ, 25-26 червня 2015 р.). — К.: НУХТ, 2015. — С.188—189.

8. Норри Д. Введение в метод конечных элементов: Пер. с англ. / Д. Норри, Ж. де Фриз. — М.: Мир, 1981. — 304 с.

9. Стренг Г. Теория метода конечных элементов: Пер. с англ. / Г. Стренг, Дж. Фикс. — М.: Мир, 1977. — 350 с.

10.Сьярле Ф. Метод конечных элементов для эллиптических задач /
Ф. Сьярле. — М.: Мир, 1980. — 512 с.

11.Шопов П.Й. Метод конденсации для задач механики несжимаемых флюидов / П.Й. Шопов // Сердика: Българско математическо списание. — 1984. — Т. 10. — С. 198—205.