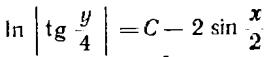Математика /4.Прикладная математика
К.п.н. Токмазов Г.В.
Государственный морской университет имени
адмирала Ф.Ф.Ушакова ,
Россия
Исследовательские задачи дифференциальных уравнений
прикладной математики морского флота
Исследовательские задачи дифференциальных
уравнений прикладной математики морского флота отражают математическое моделирование
основных элементов транспортных объектов. При этом формируется профессиональное
мышление, отражающее единство деятельностных и предметных условий в процессе
реализации исследовательских проблем прикладной математики морского флота.
Рассматриваются: циркуляция движения
морского судна; динамическое состояние такелажного троса; локальное статическое
поведение навигационного спутника; динамическое
поведение ветровой нагрузки на корпус корабля; процесс постановки судна на
якорь и другие исследовательские задачи на морском флоте.
В процессе решения исследовательских
задач дифференциальных уравнений прикладной математики морского флота необходимо
применять основные положения теории деятельности, исследовательского анализа и
теории формирования профессионального мышления.
Исследовательский анализ предполагает
выполнение последовательности познавательных аналитических действий: определить
условия анализа –задачу дифференциальных уравнений прикладной математики
морского флота (ЗДУПММФ) как целое; проанализировать условия возникновения ЗДУПММФ;
установить функциональную сложность ЗДУПММФ; определить внешние, материальные
параметры ЗДУПММФ относительно пространственных, временных, силовых,
энергетических и гравитационных характеристик; проанализировать строение
функций ЗДУПММФ; установить функциональные элементы сложности анализа ЗДУПММФ; определить
внутренние свойства и динамику ЗДУПММФ.
Задача 1
Циркуляция движения морского судна представляется локальным
дифференциальным уравнением 
.
Определить уравнение траектории движения морского судна относительно постоянных
параметров.
Ответ: 
.
Задача 2
Динамическое состояние такелажного троса
устанавливается дифферциальным уравнением 
. Определить уравнение обобщённого
перемещения троса относительно постоянных параметров.
Ответ: 
Задача 3
Локальное статическое поведение навигационного
спутника задаётся дифференциальным уравнением 
.
Определить уравнение статически возможных смещений навигационного спутника
относительно постоянных параметров.
Ответ: 
Задача 4
Динамическое поведение ветровой нагрузки на корпус
корабля представляется дифференциальным уравнением 
.
Определить эквипотенциальное уравнени перераспределения ветрового потока
относительно постоянных параметров.
Ответ: 
Задача 5
В процессе постановки судна на якорь его динамическое
состояние устанавливается дифференциальным уравненем 
. Определить уравнение кинематического
состояния якоря относительно постоянных параметров.
Ответ: 
Задача 6
Состояние генерального груза на палубе судна
соответствует диффе-ренциальному уравнению 
. Определить уравнение относительного поведения
генерального груза относительно постоянных параметров.
Ответ: 
Задача 7
Динамическое состояние швартовного троса
представляется дифференциальным
уравнением вида 
. Определить локальную траекторию швартовного
троса относительно постоянных параметров.
Ответ: 
Задача 8
Путевая модель
подводной лодки задаётся дифференциальным уравением движения 
. Определить кинематическое уравнение подводной
лодки относительно постоянных параметров.
Ответ: 
Задача 9
Динимическое уравнение сигнальной ракеты
представляется дифференциальным ууравнением 
. Определить кинематическое уравнение
сигнальной ракеты относительно постоянных параметров.
Ответ: 
Задача 10
Динамическое состояние газовой смеси в судовом
двигателе внутреннего сгорания определяется дифференциальным уравнением 
.
Определить кинематическое состояние газовой смеси относительно постоянных
параметров.
Ответ:
