ПОСТРОЕНИЕ КРИВОЙ АТОМНОГО
РАСПРЕДЕЛЕНИЯ
ДЛЯ ОЛОВА
Кажикенова
С. Ш., Асанов А.А.
Теория жидкого состояния
является не простым разделом современной теории металлургических процессов.
Если структура твердых веществ изучена на достаточном уровне и в результате
исследования их свойств получен богатейший экспериментальный материал, и этот
материал проанализирован с точки зрения квантовой физики и химии, то этого
нельзя сказать о жидкостях и жидких металлических системах вообще. Несмотря на
эти проблемы исследования в этой области непрерывно расширяются благодаря
развитию физики жидкого состояния, физической химии и теории металлургических
процессов.
В данном случае особое
значение имеют гидродинамические исследования расплавов с учетом микро - и
наноструктуры расплавленных систем. Накопленные знания в этих областях в целом
позволяют решить многие проблемы, связанные с теорией расплавленного состояния
и, очевидно, оказывают положительное влияние на прогресс физики жидкого
состояния, теории металлургических процессов и, естественно, металлургических
технологий. Эти исследования имеют большое значение, так как до сегодняшнего
дня еще не разработана не только общая теория твердого и жидкого состояний, но
также газообразного и плазменного состояний [1].
Одним из наиболее
конструктивных методов изучения физических свойств расплавов является
компьютерное моделирование. Однако для конкретных вычислений необходим
развернутый физико-математический аппарат. Для реализации такой программы
воспользуемся методами статистической физики.
Необходимо заметить, что наибольшие успехи были достигнуты в этом направлении в работах М. Борна, Г. Грина, Дж. Кирквуда, Н.
Н. Боголюбова и других. Причем основной задачей
такой статистической теории жидкостей является установление связи между
свойствами молекул и межатомным потенциалом, а также между термодинамическими и
кинетическими свойствами расплавленных
систем. При исследовании свойств
расплава необходимо учитывать,
по какому набору частиц производится
усреднение физических величин. Как известно [2,3],
в случае кристалла можно получить, например, информацию, относящуюся к одной
единственной дислокации, но
нельзя проследить за движением одного атома
примеси. А в расплавах из-за высокой подвижности его частиц и
вследствие отсутствия дальнего порядка (как в кристаллической решетке) ближайшие
окружения различных атомов или молекул могут различаться довольно сильно, как по числу соседей, так и по
их пространственному расположению. Поскольку нет возможности следить за
поведением отдельного атома или группы
атомов, так называемых кластеров, то результаты измерений любого свойства расплава оказываются
усредненными по большому числу атомов. Когда изучается свойство, не зависящее от угловой ориентировки (в
пространстве) ближайших соседей данного атома, то при усреднении по различным атомам такая ориентировка не
может быть отражена в результате измерения, так что остается существенным лишь общее число атомов, расположенных на определенном
расстоянии от данного атома.
Для описания данного положения выберем
шаровой слой с внутренним радиусом ![]() и наружным
и наружным ![]() , с центром в ядре произвольной частицы простого расплава
(содержащего для простоты лишь атомы одного элемента). В этом случае среднее число атомов, находящихся в этом шаровом слое, будет
пропорционально объему слоя
, с центром в ядре произвольной частицы простого расплава
(содержащего для простоты лишь атомы одного элемента). В этом случае среднее число атомов, находящихся в этом шаровом слое, будет
пропорционально объему слоя ![]() и определяется следующим соотношением:
и определяется следующим соотношением:
![]() ,
(1)
,
(1)
где ![]() - так называемая
парная функция радиального распределения.
- так называемая
парная функция радиального распределения.
Функция ![]() по своему
физическому смыслу является плотностью числа частиц, но не средней, а локальной
по отношению к некоторому произвольному атому, выбранному в качестве начала
координат. В случае, когда расстояние
по своему
физическому смыслу является плотностью числа частиц, но не средней, а локальной
по отношению к некоторому произвольному атому, выбранному в качестве начала
координат. В случае, когда расстояние ![]() достаточно большое по сравнению с межатомным
расстоянием
достаточно большое по сравнению с межатомным
расстоянием ![]() , то отдельные
атомы, возможно, не будут испытывать действия центральной частицы и, поэтому
будут располагаться независимо от нее. В этом случае мы должны подставить в
уравнение (1) вместо
, то отдельные
атомы, возможно, не будут испытывать действия центральной частицы и, поэтому
будут располагаться независимо от нее. В этом случае мы должны подставить в
уравнение (1) вместо ![]() обычную среднюю
плотность
обычную среднюю
плотность ![]() В случае, когда расстояние от центра данного атома слишком мало
(меньше так называемого диаметра атома), то в шаровой слой не попадет ни одного ядра частицы. Функция
В случае, когда расстояние от центра данного атома слишком мало
(меньше так называемого диаметра атома), то в шаровой слой не попадет ни одного ядра частицы. Функция ![]() имеет при небольших расстояниях
имеет при небольших расстояниях
![]() осциллирующий характер. Именно такое поведение соответствует структуре расплава,
так как в них должны проявляться некоторые
черты упорядочения, свойственные кристаллу, из которого данный расплав образовался. Таким образом, должно существовать предпочтительное расстояние между ближайшими
соседями, аналогичное межатомному
расстоянию в кристалле, среднее число ближайших соседей, аналогичное координационному числу в решетке, и так
далее. Существование элементов упорядочения в расплаве, обусловленное, в конечном счете, собственным объемом молекул и особенностями межатомного потенциала,
определяется термином «ближний порядок».
Если бы мы рассматривали идеальный
газ, то вместо осциллирующей кривой
функция радиального распределения
осциллирующий характер. Именно такое поведение соответствует структуре расплава,
так как в них должны проявляться некоторые
черты упорядочения, свойственные кристаллу, из которого данный расплав образовался. Таким образом, должно существовать предпочтительное расстояние между ближайшими
соседями, аналогичное межатомному
расстоянию в кристалле, среднее число ближайших соседей, аналогичное координационному числу в решетке, и так
далее. Существование элементов упорядочения в расплаве, обусловленное, в конечном счете, собственным объемом молекул и особенностями межатомного потенциала,
определяется термином «ближний порядок».
Если бы мы рассматривали идеальный
газ, то вместо осциллирующей кривой
функция радиального распределения ![]() была бы постоянной и равной средней
плотности
была бы постоянной и равной средней
плотности ![]() , так как
частицы идеального газа не взаимодействуют
и имеют нулевой собственный объем. К примеру, функция радиального распределения
для жидкого олова представлена в соответствии с рисунком 1.
, так как
частицы идеального газа не взаимодействуют
и имеют нулевой собственный объем. К примеру, функция радиального распределения
для жидкого олова представлена в соответствии с рисунком 1.
Заметим, что кроме самой функции ![]() часто рассматривают величину:
часто рассматривают величину:
![]()
Парабола представляет собой график ![]() , к которому асимптотически стремится
, к которому асимптотически стремится ![]() при больших расстояниях
при больших расстояниях
![]() . Вертикальные
линии описывают случай кристалла, когда расстояния между
атомами фиксированы, причем высота линии пропорциональна числу соседей в соответствующей координационной сфере. Эти результаты
можно представить так, что при плавлении кристалла пики размываются, образуя изображенную в
соответствии с рисунком 1 осциллирующую функцию
. Вертикальные
линии описывают случай кристалла, когда расстояния между
атомами фиксированы, причем высота линии пропорциональна числу соседей в соответствующей координационной сфере. Эти результаты
можно представить так, что при плавлении кристалла пики размываются, образуя изображенную в
соответствии с рисунком 1 осциллирующую функцию ![]() . Причины осцилляции при
малых расстояниях могут быть трактованы как наиболее вероятное расположение
атомов в расплавах при увеличении
. Причины осцилляции при
малых расстояниях могут быть трактованы как наиболее вероятное расположение
атомов в расплавах при увеличении ![]() .
.
![]()
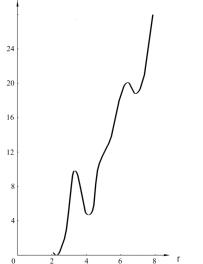
Рисунок 1 – Кривая
атомного распределения для олова
Таблица 1 – Кривая атомного
распределения для олова
|
|
2.1 |
2.3 |
2.5 |
3 |
3.5 |
4 |
4 |
5 |
5.3 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
|
|
0.3 |
0 |
0.5 |
5 |
9.8 |
6 |
5.8 |
11.5 |
12.7 |
13 |
18 |
20.1 |
18.8 |
21 |
28 |
Литература
1 Малышев В. П.,
Абдрахманов Б. Т., Нурмагамбетова А. М. Плавкость и пластичность металлов. –
М.: Научный мир, 2004. – 148 с.
2 Регель А. Р., Глазов
В. М. Физические свойства электронных расплавов. – М., 1980. – 296 с.
3 Ахиезер А. И.,
Петлеминский С. В. Методы статистической физики. – М.: РФМ Наука, 1977. – 368
с.