ОБ ОДНОМ АЛГОРИТМЕ РАСЧЕТА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ДЛЯ МЕТАЛЛИЧЕСКИХ РАСПЛАВОВ

 

Кажикенова С.Ш.

 

Ранее нами была определена парная функция радиального распределения  , описывающая среднее размещение частиц расплава вокруг некоторого произвольного атома. Теперь это необходимо обобщить на случай, когда нас будут интересовать взаимные расположения числа атомов. Для этого выберем в расплаве объем  . Пусть среднее число частиц в этом атоме окажется равным    где   - плотность числа частиц (число частиц в единице объема). Если считать  достаточно малым, то  будет намного меньше единицы. Вследствие этого, произведение  можно рассматривать как вероятность обнаружения частицы расплава в объеме :        Выделим в расплаве следующие элементы объема   и   вблизи точек с радиус – векторами Определим вероятность того, что в объемах    и   одновременно будут находиться две частицы. Тогда эта вероятность должна быть пропорциональна самим объемам, то есть:

                                                                                        (2)

где функция  так называемая бинарная корреляционная функция.

Если предположить, что объемы  и   расположены далеко друг от друга, то вероятности попадания частиц в эти объемы становятся независимыми и по теореме об умножении вероятностей можно записать:

    

Из  соотношений  (2)   видно, что  при больших величинах   следует   Точно также, аналогично сказанному выше, можно ввести вероятность    того, что в объемах     окажется по одной частице. Определим         следующим образом:

 .                                                         (3)

  Введенная уравнением (3) функция координат всех  частиц , называется корреляционной функцией  – го порядка. Как и раньше, при увеличении расстояния между каждыми двумя объемами, вероятности нахождения частиц в каждом объеме становятся независимыми, то есть при  очевидно, что   Нужно подчеркнуть что, частный случай корреляционной функции      -го   порядка — это,  так  называемая,  тернарная корреляционная функция   

Кроме этого, можно установить связь между бинарной корреляционной      функ­цией и парной функцией радиального распределения .                                            Вероят­ность нахождения двух частиц в объемах     и     можно предста­вить в виде произведения двух вероятностей: во-первых, что в объеме                 окажется одна частица  -  и, во-вторых, что на расстоянии     от первой частицы окажется вторая  - . Таким образом,     — это вероятность второго события при условии, что первое уже наступило:

 

Вероятности   могут быть нормированы   следующим образом:

 

где   — полное число частиц расплава.

  

и соответственно:

   

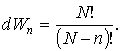
На практике для удобства расчетов целесообразно переформулировать корреляционные функции и вероятности так, чтобы первые стали безразмерными и чтобы нор­мировочные интегралы равнялись единице. Для этого мы вводим новые вероятности заданной конфигурации  п -  частиц расплава:

                                                             (4)

где             — координаты  той частицы.

Определенная таким образом корреляционная функция, естественно, является безразмерной. Далее можно будет потребовать, чтобы новая вероятность нормировалась на единицу        т. е.

                                                                 (5)

Из уравнений    (4)    и    (5)    видно, что:

   

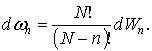
Последнее уравнение  подсказывает достоверную трактовку вероят­ностей           . Вероятность  относится к данной конфигура­ции объемов    когда является несущественным, какие именно частицы занимают эти объемы. Объем   отно­сится к любой из N частиц, а объем    — к любой из оставшихся  частиц и так далее. Вследствие этого и появляется дополнительный мно­житель 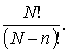  С учетом  соотношений  (3)  и  (5), находим связь между корреляционными функциями      и   :

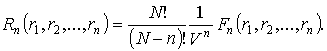                                                 (6)

Отметим, что корреляционные функции двух последую­щих порядков связаны между собой соотношением (6), вытекающим из определения вероятности. Введем теперь полную потенциальную энергию системы, зависящую от координат всех частиц расплава. В силу этого, согласно статистике Больцмана – Гиббса, вероятность данной кон­фигурации частиц пропорциональна фактору    . Следо­вательно:

 

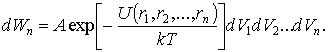
Таким образом, корреляционную функцию    можно определить                  из потенциальной энергией системы. Тогда можно построить рекуррентные соотношения  для  ,  которые  позволяют найти корреляционные функции низших порядков:

 

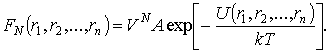
Вычисление указанных интегралов в настоящее время может быть легко проведено пока лишь для газов, у которых плотность частиц мала. А прямое определение корреляционных функций расплава с помощью статистической механики выполнить довольно трудно. В таких случаях прибегают к численным методам, таким как метод Монте – Карло, используя возможности компьютерной техники. Предположим, что нас интересует среднее значение некоторого экстенсивного физического свойства расплава    определяемого взаимным расположением группы из п - частиц. В раз­личных областях расплава   конфигурации будут отличаться друг от друга, так что значения свойства   будут колебаться вокруг этого среднего значения. Поскольку вероятность расположения частиц в   – конфигурации описывается корреляционной функцией   то усреднение величины    выполняется  инте­грированием с весом   :

В расплаве, содержащем N частиц, число различных групп из п - частиц равно 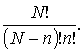   Поэтому значение свойства       для всего объема расплава будет равно:

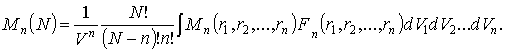
Наиболее часто рассматривают свойства, зависящие либо от координаты одной частицы, либо от взаимных расстояний пар частиц, то есть свойства, определяемые парными взаимодей­ствиями. В первом случае:

Из уравнения (6) следует, что  ,        поэтому:

Для свойства, определяемого парными взаимодействиями, можно записать:

После некоторых преобразований имеем:

Обозначая     через ,  запишем:

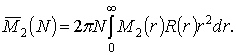                                                                             (7)

Важным примером применения уравнения   (7)  является вычис­ление полной энергии расплава в приближении, когда потенциальная энергия системы может быть представлена в виде суммы энергий парного взаимодействия частиц. Если парный потенциал обозначить через    и учесть, что средняя кинетическая энергия одноатомной частицы равна , то для полной энергии справедливо следующее соотношение:

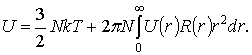
Описанные выше результаты показывают, что знание корреля­ционных функций       необходимо для расчета целого ряда термодинамических свойств металлического расплава.