Technical science/2. Mechanics

Dr. Sc. Techn., professor Gots A. N.

Vladimir state University of a name Alexander Grigorievich and Nikolai Grigorievich Stoletovs, Russia

New schematized diagram of limit cycles under the action of normal stresses

Calculation of factors of safety of machine parts under the action of normal stresses in the case of uniaxial stress state and the asymmetric cycle of loading with amplitude σ_a and mean stress σ_m is performed on the basis of dependency S. W. Serensen, and R. S. Kinasoshvily [1]:

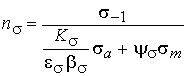, (1)

where K_σ is the effective stress concentration factor; ε_σ – scale factor; β_σ – coefficient of the surface layer; ψ_σ – coefficient of influence of cycle asymmetry or coefficient, which characterizes the sensitivity of the material to the asymmetry of the cycle [2] .

The maximum amplitude of the stresses σ_ra for laboratory sample with asymmetric cycle of loading can be expressed by the equation, well the corresponding experimental data in the range of variation of the coefficient of asymmetry

, (2)

where σ_rm is the current value of the limiting medium stress of cycle.

In computational practice, often use a schematized diagram of the limiting amplitudes Serensen-Kinasoshvily in which the coefficient ψ_σ equal

, (3)

where σ₀ is the fatigue limit of laboratory samples in a pulsating cycle.

Because the value of σ₀ in the reference literature is not given, it is recommended to define her by the approximate formulas [3]. For steels in bending and tension-compression . Upper limits refer to mild steels. It is easy to notice that with this choice of σ₀, after substitution in (3) the coefficients ψ_σ will be constant, independent of the mechanical characteristics of the material.

In [1] for steels calculation ψ_σ it is proposed that the formula

, (4)

where σ_v is the tensile strength, MPa.

From (4) it follows that ψ_σ varies from 0.1 at σ_v = 400 MPa, while σ_v = 1500 MPa to 0.32.

The value of ψ_σ can be determined by constructing the author's proposed new schematized diagram of limit cycles s_ra = f(s_rm). To do this, use for limit cycles linear dependence Goodman [4]

, (5)

and parabolic Gerbera [4]

. (6)

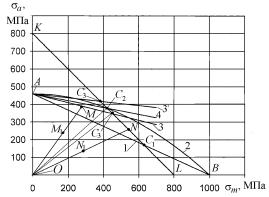
Fig. 1. Chart of the limiting amplitudes for steel 40XH: 1 – direct of Goodman; 2 – Gerber parabola; 3 – marginal direct Serensen-Kinasoshvily(s₀ = 1,6s_-1); 4 – proposed direct s₀ = 1,8s_-1; 3’ – the same when s₀ = 1,6s_-1 4 – proposed direct schematized diagram

In Fig.1 for steel 40XH (with the characteristics of mechanical strength in MPa: tensile strength σ_v =1000; yield strength σ_0,2=800; endurance limit of a symmetric cycle σ_-1=460) the diagrams of the limiting amplitudes using the dependences (5) – direct 1 and (6) – curve 2.

For parts made from plastic materials according to (5) and (6) are valid as the threat to them is s_ra = f(s_rm) only on a portion of the chart not only fatigue, but also the transition for the yield strength, which leads to residual deformations that distort the shape and dimensions of the part.

Therefore, the maximum stress cycles must be less not only endurance limit, and yield strength s_max = s_a + s_m < s_0,2.

In order to exclude from the chart s_ra = f(s_rm) the area where the limiting maximum stress σ_rmax=s_ra + s_rm > s_0,2, take the straight line KL, which cuts off on the cuts the coordinate OL and OK is equal to the yield strength (steel 40XH s_0,2 = 800 MPa, Fig. 1). The equation of a line KL is:

. (7)

Thus, for the parts made of plastic materials chart limit amplitude in the coordinate axes s_m-s_a is limited by the line 1 and the parabola 2 (Fig. 1) until they intersect at the points C₁ and C₂ with direct KL, and more – direct C₁L or C₂L. The coordinates of the points of the broken lines AC₁L or AC₂L give limit values and depending on the selected function s_ra = f(s_rm).

Replace plot charts Goodman and Gerber schematized diagrams. In Fig.1 by equation (2) with (3) built direct limit Serensen-Kinasoshvily 3, assuming ψ_σ= 0,11) and 3’, ψ_σ= 0.25 to crossing them with direct KL at the points and respectively. Note that the direct limit (if taken ) will be above the Gerber parabola, which contradicts the results of studies P. Forrest [4].

For steel 40XH, using (4), find the value of ψ_σ= 0,22. Limit direct, built according to (4), in this case almost coincides with the straight 3’ (Fig. 1).

Build a schematized diagram using three points σ_0,2, σ_-1 and the coordinates of the point of intersection C₂ () Gerber parabola with a straight KL. Combine in a system of dependency (7) and (8), after the decision of who will receive the coordinates of the point C₂ ():

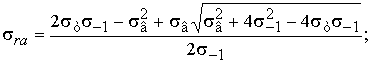(8)

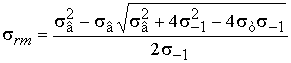. (9)

Connecting points A and C₂( ), get a new schematized diagram OAC₂L (Fig. 1) in which the tangent of the slope of the straight AC₂ to x-axis , considering the influence y_s is numerically equal to the coefficient of medium stress (constant component of the cycle) at the limit of endurance:

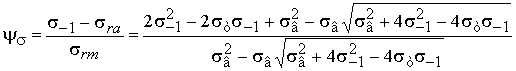. (10)

When calculating the value y_s according to the formula (10) are used, only those characteristics of mechanical strength, which are listed in the reference literature.

Formulas (8) and (9) allow us to determine what type of destruction is dangerous for a known working medium s_m and the amplitude s_a stresses.

If during the calculation details s_m/ s_a < s_rm /s_ra , the duty cycle of stresses is in the field OAC₂ (Fig. 1) and calculate the factor of safety should be based on (1). If s_m/ s_a > s_rm /s_ra, the calculation is based on [1-3]:

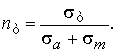(11)

The values of the coefficients ψ_σ and relations limit s_rm /s_ra, can be defined by the formulas (9), (10) and (11) for steels, if known mechanical characteristics of the materials.

In our proposed schematized diagram direct limit AC₂ is located between the parabola 2 and 1 direct, i.e., it satisfies the experimental data for ductile metals [4, 5].

LITERATURE

1. Kogaev V. P., Makhutov N. A., Gusenkov A. P. Calculations of machine parts and structures for strength and durability: Handbook – M.: Mashinostroenie, 1985. – 224 p.

2. Birger I. A., Shorr B. F., Iosilevich G. B. Calculation of the strength of machine parts. Handbook. – M.: Mashinostroenie, 1993. – 640 p.

3. Handbook on strength of materials // M. N. Rudizin, P. Y. Artemov, M. I. Lyuboshitz.; Under the editorship of M. N. Radizina. – Minsk: Vysheishaya school, 1970. - 630 p.

4. Forrest P. Fatigue of metals. Translation from English. Under the editorship of S. V. Sorensen. – M.: Mashinostroenie, 1968. – 352 p.

5. Collins J. Damage of materials in structures. Analysis, prediction, prevention: Trans. from engl. – M.: Mir, 1984.– 624 p.

6. Gots A. N. The calculations of the strength of engine parts with voltages, variable in time/A. N. Gots – 3-e Izd. – M.: FORUM; infra-m, 2013 – 208 p.http://www.translate.ru/%28%F2%E0%EChttp://www.translate.ru/%28%F2%E0%EC