Technical
sciences / 5. Energy
Ph.D. Solntseva A.V., Ph.D. Borminsky S.A.
Samara State Aerospace University, Russia
System for remote monitoring of
liquids stored in pools and tanks
Plants of oil-extracting, oil-processing,
aircraft, medical and
food industries need to organize remote control of liquids,
stored or transported in pools and tanks. Main control parameters are level and
density of liquids.
Picture 1 shows Tank 1 with liquid to be monitored. Wave
Guide 2 is installed inside the tank. Acoustic Sensor 3 is set at an open end of the wave
guide. It receives sounding impulses from Generator 4. Data collected from Acoustic
Sensor 3 and from Generator 4 go to Data Collecting Unit 5. Data Collecting Unit
5, Analog-Digital Converter Unit 6, Spectrum Analysis Unit 7, Level Calculating Unit 8 and Density
Calculating Unit 9 are in series connection to process information received.
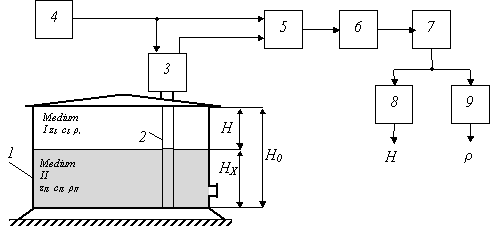

Picture 1 - Block diagram of system
for remote monitoring of liquids' parameters
Tank 1 is filled with liquid to be monitored (Medium
II), empty part of tank is filled with Medium I. Generator 4 sends a sounding
pulse p(0,t) to Acoustic Sensor 3. This
pulse is an energy bunch, that stimulates around vibration set of variable frequencies.
Its spectral density is described by Fourier transformation:
 . (1)
. (1)
Pulse spreads
in Medium I inside the Wave Guide 2 till medium boundary. Its form at medium boundary and
at current level of liquid in tank is described by the following expression:
 , (2)
, (2)
Its spectral density:
![]() (3)
(3)
where Í – is distance to medium boundary,
kI(jω) - is
a wave vector of Medium I, in which the sounding pulse is being spread. It is
described by the following expression:
![]() (4)
(4)
where ñ - is phase acoustic velocity,
r - medium density,
b - dissipative coefficient.
The signal is reflected from medium boundary. Reflectance coefficient of acoustic signal at the boundary,
at normal fall, absorption by medium not taken into consideration, is described
by the following formula:
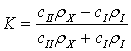 , (5)
, (5)
where
cI, cII, ρI,
ρÕ – acoustic velocities and
densities of contacting mediums.
Acoustic velocity c in a medium
is seen as a polynomial dependence from density, and in general is described by
the following expression:
![]() . (6)
. (6)
For
oil-products with relative density from 0,651 to 1,076 kg/m3 this
analytical dependence is expressed as follows:
![]() . (7)
. (7)
For
any group of liquid products a linear dependence
can be found. It will bind acoustic velocity in the medium and its density. For
example, for heavy oil-products with relative
density ranging from 0,8 – 0,95 kg/m3 dependence can be set as
linear:
![]() (8)
(8)
where ÊÑ =1654 [m4/s·kg]– is a coefficient of
correlation between density and acoustic velocity.
Form
of the signal, reflected from Medium II, at the moment when it returns to its
radiation point, is described by the following expression:
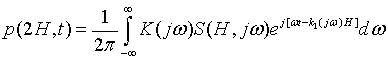 (9)
(9)
Reflected
signal is received in Data Collecting Unit 5. It is converted into electric
signal p(2Í,t). Also, sounding signal
from Generator 4 is sent to the input of Data Collecting Unit 5. In
Analog-Digital Converter Unit 6 the signals are converted correspondently. Digital
signals are Fourier-transformed in Unit 7.
Spectrum
densities of sounding signal and signal reflected from Medium II, that has
passed 2Í distance (from its emission
point to Medium II boundary and backwards), are bound by the following expression:
![]() (10)
(10)
Expression
(8) states, that level and density are correlated with signals' spectral densities,
taking into account (7), by the
following relations:
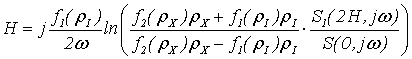 , (11)
, (11)
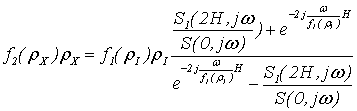 . (12)
. (12)
Spectrum
densities of sounding and reflected signals are complex variables. In Spectrum
Analysis Unit 7 they are decomposed into amplitude and phase components.
Equating
relations ![]() and
and ![]() , represented in exponential form and in form (10), we
will derive the following expression:
, represented in exponential form and in form (10), we
will derive the following expression:
 . (13)
. (13)
Thus, data about amplitude and phase components
![]() ,
,![]() ,
,![]() ,
,![]() is used to calculate level and
density variables in Units 8 and 9. When measuring, from amplitude and phase frequency range, we take the frequency, at
which calculation is made (frequency selection ωi). Frequency i-selection means definite spectrum
component values
is used to calculate level and
density variables in Units 8 and 9. When measuring, from amplitude and phase frequency range, we take the frequency, at
which calculation is made (frequency selection ωi). Frequency i-selection means definite spectrum
component values ![]() ,
,![]() ,
,![]() ,
,![]() , taken at frequency ωi.
, taken at frequency ωi.
Distance
Í from sensor to
medium boundary is calculated in Unit 8. Forms (13) and (4) are used. Besides, the fact that complex numbers are equal, provided
their real and imaginary components are equal, is taken into consideration. The
following expression is used:
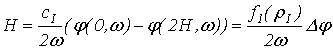 . (14)
. (14)
The
following formula calculates the level of Medium II in tank:
HX=H0-H. (15)
Medium
II density is calculated in Unit 9 according to this expression:
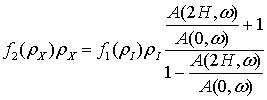 . (16)
. (16)
There
are cases, when measurement matter allows
to compose linear dependence between acoustic velocity and density as shown in
(6), as for example for heavy oil-products in expression (8). Then density is calculated
by the following expression:
 , (17)
, (17)
where d0,
d1 - are polynomial coefficients (6) for Medium I,
a0, a1 - are polynomial coefficients
(6) for Medium II.
As for accuracy
of methods suggested, at tank Medium II level equal to 1m, level measurement absolute
error is 1.5 sm, while density measurement relative reduced error is 4.5%.
Reference
1. Solntseva A.V., Borminsky S.A. Measurement method of tank infill
based on spectrum analysis of acoustic impulse reflected from the controlled
medium // Volga Region Scientific and technical Bulletin. – 2014. – ¹6. – P.
348-351.
2. Solntseva A.V., Borminsky S.A., Skvortsov B.V. Method
Controlling Density of Liquid Medium
Based on Spectral Characteristics of Reflected Acoustic Impulses // Samara
Scientific Center of RAS bulletin. – 2014. – V.16. - ¹6. – P.85-88.