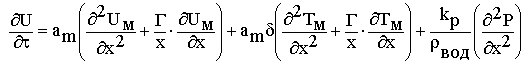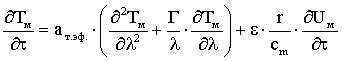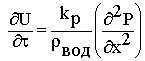Технические науки/5. Энергетика

К.т.н. Садртдинов А.Р.

Казанский национальный исследовательский технологический университет (ФГБОУ ВПО «КНИТУ»), Россия

Моделирование процесса сушки слоя зернистой биомассы в установках с кондуктивным подводом тепла

Процессы сушки, протекающие в установках термической переработки сырья, в частности древесной биомассы, являются весьма критичными, так как могут оказывать влияние на процесс переработки в целом. Основными характеристиками процесса сушки является вид подводимого тепла и его интенсивность, особенно это важно при сушке слоя зернистой биомассы [1]. В ряде случаев сушка зернистых материалов осуществляется при кондуктивном подводе тепла, что требует введения некоторых допущений при рассмотрении данного процесса сушки.

В работе рассмотрен более распространенный процесс применения кондуктивного подвода тепла при сушке зернистой биомассы, а именно в цилиндрической камере с температурой стенки более 200°С [2].

Для определения изменения влажности зернистой биомассы по слоям с течением времени, целесообразно использовать дифференциальное уравнение А.В. Лыкова [3]

(1)

в котором основными градиентами являются температура и давление.

Изменение температуры сырья по слоям можно описать дифференциальным уравнением энергии [4]

(2)

С учетом высокой температуры процесса сушки и как следствие значительного преобладания малярного переноса по отношению к диффузионному можно преобразовать выражение (1) в следующее уравнение

(3)

где градиентом изменения влажности сырья является разность давлений паров внутри и на поверхности частиц.

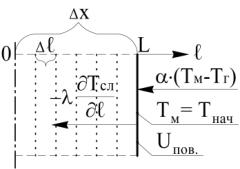
Для решения уравнения (2) начальные и граничные условия, схематично изображенные на рис. 1, запишутся в виде

Рис.1. Схема граничных условий

процесса сушки слоя материала

	(4)
	(5)

В свою очередь условия для решения уравнения (3) запишутся следующим образом. Начальные условия примут вид

; ,

(6)

а граничные условия по влажности на поверхности частицы, запишутся уравнением [5]

(7)

где j – относительная влажность среды (с учетом высокой температуры процесса и быстрого испарения влаги j ≈ 1).

Для решения предложенной системы дифференциальных уравнений необходимо знать поле давлений в различных слоях материала, которое можно определить из выражения, полученного с учетом преобразования уравнения Менделеева-Клапейрона

(8)

где σ – порозность материала, Т_м – температура сырья, U_k – влажность сырья, ρ – плотность, R – универсальная газовая постоянная.

Особенностью предложенного математического описания процесса кондуктивной сушки зернистой биомассы, является осуществление расчета сушки заданного слоя на основе расчета сушки частиц входящих в данный слой. Таким образом в процессе расчетов происходит цикличный переход от слоя к частице и обратно. Как следствие такое моделирование применимо для сушки любого сыпучего зернистого сырья.

Представленные результаты получены в рамках реализации гранта Президента РФ по поддержке молодых ученых, шифр темы МК-3434.2015.8 (договор № 14.Z56.15.3434-МК от 16.02.2015 г.).

Литература:

1. Садртдинов, А.Р. Совершенствование техники и технологии процесса газификации отходов деревообработки : дисс. канд. тех. наук // Казан. нац. исслед. технол. ун-т. Казань, 2011. – 139 с.

2. Тунцев Д.В. Схема контактного пиролиза отходов лесозаготовки / Д.В. Тунцев, Р.Г. Хисматов, А.М. Касимов, И.С. Романчева, А.С. Савельев // Актуальные направления научных исследований XXI века: теория и практика. Воронеж, 2014. – № 2-3(7-3). – С. 146-149.

3. Лыков, А.В. Теория сушки / А.В. Лыков. – М.: Энергия, 1968. – 472 с.

4. Исмагилова, Л.М. Математическое описание стадии пиролиза с кондуктивным подводом тепла при газификации древесного сырья / Л.М. Исмагилова, А.Р. Садртдинов // Актуальные направления научных исследований XXI века: теория и практика. Воронеж, 2014. – Т.2. – №5-4. – С. 115-119.

5. Шубин, Г.С. Сушка и тепловая обработка древесины / Г.С. Шубин. – М.: Лесн. пром-сть, 1990. – 336 с.