MATHEMATICS / 3. Theory of Probability and Mathematical Statistics

Iskakova A.S., Zhaxybayeva G.K.

L.N. Gumilev Eurasian National University, Astana, Kazakhstan

About maximum likelihood estimates of one class of discrete multinomial distributions

As is know, maximum likelihood estimates, under certain conditions [1], have important properties in the theory of estimation. In other words, they are consistent, asymptotically normal, and asymptotically effective.

Let us consider the case when the maximum likelihood estimates do not always exist. Suppose that the urn contains balls, and each ball in the urn is marked by some value of a rectangular matrix L_a, where the elements of matrix l_ai are arbitrary integers from a known finite set. Suppose that the number of possible matrices L_a is d. Let’s the elements of the vector p=(p₁, … , p_d) determine the probabilities of retrieval from the urn of a ball marked by corresponding matrices L₁, …, L_d, moreover .

There is a successive extraction of n balls from the urn with a return, and it is not known which balls were taken from the urn. Only the value of the matrix u is know, which represents the sum of the matrices on n balls taken from the urn. To study this situation, it is necessary to construct a probability distribution u. Let`s say, that V_u represents the number of possible combinations r_1vuL₁,…, r_{d vu}L_d, which in the sum formed a matrix u, where r_1vu,…, r_{d vu} determine the possible number of removed balls that are marked with the corresponding matrices L₁,…, L_d. In other words, from work [2] follows that V_u is the number of partitions of the matrix u into parts L₁,…, L_d. The following assertion follows from the results of [3-5]. The probability that the random variable U will take the value of the matrix u, is

(1)

Obviously, in practice, the elements of the vector are not known p=(p₁, …, p_d). Consequently, formula (1) does not find actual application. In this connection, it becomes necessary to determine the probability estimate (1).

Let Х represents a sample of the volume k from the distribution (1) and х there are observed values of X, where the elements х_i represent the sum of matrices on n balls sequentially removed from the urn with a return. For each i=1, ..., k determine V_i number of partitions х_i for matrices L₁, … , L_d. Let us find the maximum likelihood estimates for the parameters p₁, … , p_d of the distribution (1). The log-likelihood function for the parameters p₁, … , p_d of the distribution (1) can be represented in the formwhere From which it follows that for any Δ=1, ¼ , d we have

(2)

where under i=1, … , k, v_i=1, … , V_i

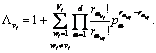(3)

As is known, maximal likelihood estimate for parameters p=(p₁, … , p_d) satisfy the following condition under Δ=1, ¼ , d

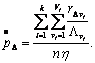(4)

As then

(5)

By (3) it is obvious that L_vi³1, under i=1, … , k, v_i=1, … , V_i, moreover L_vi=1, if V_i=1, otherwise L_vi>1. From which it follows thatthat is if at some i=1, …, k L_vi>1. Hence (6) is satisfied if V_i=1 for all i=1, …, k. Therefore, the construction of maximum likelihood estimates for the distribution parameters of the presented model is possible only if the elements of the sample implementation have no more than one partition into the presented parts. In other words, if for all i=1, …, k V_i=1, то L_vi=1, with Δ=1, ¼, d, that is

(6)

Thus, the following theorem is true.

Theorem. If all the elements of the sample implementation х from the distribution (1) have no more than one partition into the presented parts, then there exist maximum likelihood estimates for the distribution parameters (1), defined as

Consequence. If any element of the sample implementation х from the distribution (1) has more than one partition into the presented parts, then there are no maximum likelihood estimates for the distribution parameters (1).

Thus, it is not always possible to construct maximum likelihood estimates for the distribution parameters (1).

Reference

1. Ibragimov I. A., Has' Minskii R. Z. Statistical estimation: asymptotic theory. – Springer Science \& Business Media, 2013. – Т. 16.

2. Ayman I. Construction of the most suitable unbiased estimate distortions of radiation processes from remote sensing data //Journal of Physics: Conference Series. – IOP Publishing, 2014. – Т. 490. – №. 1. – P. 012113.

3. Ayman I. Statistical Research for Probabilistic Model of Distortions of Remote Sensing //Journal of Physics: Conference Series. – IOP Publishing, 2016. – Т. 738. – №. 1. – P. 012004.

4. Iskakova A. S. Determination of the most suitable unbiased estimate for a weather forecast being correc //Sibirskii Zhurnal Industrial'noi Matematiki. – 2002. – Т. 5. – №. 1. – P. 79-84.

5. Maximum likelihood estimation and inference for approximate factor models of high dimension //Review of Economics and Statistics. – 2016. – Т. 98. – №. 2. – P. 298-309.