Современные информационные технологии/2. Вычислительная техника и программирование

Д.т.н. Романюк О.Н. Ляч А.А.

Вінницький національний технічний університет, Україна

Визначення опуклості багатокутника

Рендеринг полігональних областей передбачає розбивку вихідного полігона на складові трикутники. Якщо багатокутник опуклий процедури тріангуляції істотно спрощуються [1-3]. У зв'язку з цим актуальними є питання розробки ефективних алгоритмів визначення опуклості полігонів для задач рендеринга. Задача визначення опуклості полігонів є також складовою для дво- і тривимірного відсікання [1].

Пропонується алгоритм визначення опуклості полігона, заснований на обчисленні коефіцієнта нахилу сторони полігона до вісі . Згідно алгоритму задається первісний напрямок обходу полігона, наприклад, проти часової стрілки. Вершини з абсцисами і поділяють полігон на дві частини: верхню і нижню. При обході полігона в напрямку проти часової стрілки, до нижньої частини відносяться сторони, абсциси вершин яких лежать від до , а до верхнього - від до (рис.1.). При цьому для частини контуру на проміжку від до кут нахилу сторін до вісі змінюється від 90^о до 180^о, а на проміжку [-] від 0^о до 90^о. У такий спосіб можна сформувати умову опуклості:

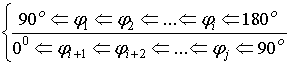(1)

де φ_i - кут при -й вершині, утворений двома сторонами.

Чи, виразивши через φ:

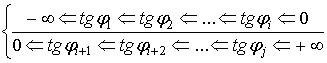(2)

Об'єднана умова для нижньої частини полігона, при обході проти часової стрілки має видгляд:

(3)

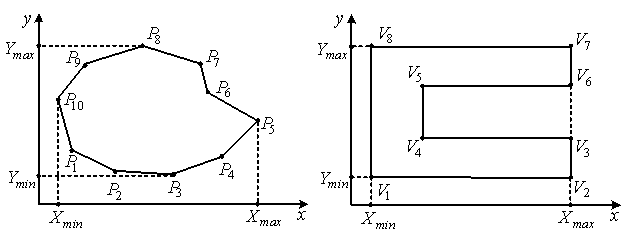
Рис.1. Визначення факту опуклості полігонів

З огляду на те, що , де - кут при -й вершині, - коефіцієнт нахилу сторони, що входить в -у вершину (з врахуванням обраного напрямку обходу) можна записати:

(4)

При цьому, якщо вершина входить до складу неопуклого багатокутника, тобто , дотримується; умова , де k₁ і k₂ - коефіцієнти нахилу сторін відповідно, що входить і що виходить з вершини.

Таким чином, тангенс кута нахилу сторін опуклого полігона для розглянутої частини контуру змінюється від -∞ до +∞ переходячи через 0, тобто, не зменшується. При одержанні k₁ > k₂ , робимо висновок, то полігон неопуклий.

Умова опуклості для верхньої частини полігона співпадає з виразом (3). Таким чином, алгоритм полягає в послідовному обході сторін багатокутника в обраному напрямку й обчисленні коефіцієнта нахилу сторони до вісі Ох. Якщо для якої-небудь сторони порушується умова опуклості (3), алгоритм припиняє роботу. Порушення умови (3) є достатнім для твердження, що заданий полігон неопуклий.

Функція складності запропонованого алгоритму складає О(Мn), при цьому, коефіцієнт при n в два рази менше, ніж для алгоритму [1]. Це обумовлено тим, що на перевірку кожної сторони затрачається тільки одна "довга" операція (розподіл). Слід також зазначити, що сторони перевіряються тільки доти, поки не зустрінеться неопукла вершина. При перебуванні такої вершини, потреба в перегляді інших вершин відпадає.

Запропонований алгоритм забезпечує визначення опуклості вигнутих (Г и П - подібних) областей, через те, що і вибираються як вершини, що мають додатково найбільші ординати. Наприклад, на рис.1 як варто вибрати вершину V₈, – V₇ при цьому вигин полігона попадає в одну частина контуру (верхню чи нижню) , що при перегляді сторін приводить до порушення умови опуклості для заданої частини контуру, а значить і для всього контуру.

Таким чином, у порівнянні з відомим алгоритмом [1], запропонований алгоритм відрізняється більш високою ефективністю; меншими обчислювальними витратами і може бути використаний для реалізації високопродуктивних засобів машинний графіки.

Литература:

1. Романюк О. Н. Комп’ютерна графіка. Навчальний посібник / О. Н. Романюк — Вінниця: ВДТУ, 2001. — 129 с.

2. Романюк О. Н. Дослідження граничних ефектів при тріангуляції областей, обмежених полігонами / О. Н. Романюк, А. В Чорний, Т. А Замковий // Вiсник Вiнницького полiтехнiчного iнституту. — 2002. — № 3. — С. 78— 86.

3. Романюк А. Н. Алгоритмы триангуляции / А. Н. Романюк, А. Г. Сторчак // Компьютеры + программы. — 2001. — № 1. — С. 35—37.