ТЕХНИЧЕСКИЕ НАУКИ/12.Автоматизированные системы управления на производстве.

Д.т.н., профессор Бейсенби М.А., докторант PhD Закарина А.Ж., докторант PhD Булатбаева Ю.Ф.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Элементы теорий катастроф

 

Типичной моделью динамической системы является обыкновенное дифференциальное уравнение

,                                                             (1)

где  - переменная состояния, - некоторая функция состояния, характеризующая закон эволюции, - параметр системы. Если задано начальное состояния , то существует единственное решение уравнения (1), которое предсказывает будущее состояние  для любых  .

В связи с тем, что проблема устойчивости связана с анализом реакции системы на малое возмущение ее состояния [1], на первом этапе она может быть исследована в рамках линейного приближения (первый метод Ляпунова), заключающееся в следующим. Пусть  есть некоторое частное решение уравнение (1). Для устойчивости этого решения (состояния) введем в рассмотрение переменную , которая задает малое отклонение от частного решения:

,                                                               (2)

(здесь  - возмущенное решение).

Задача состоит в исследовании эволюции во времени малого возмущения , которая подчиняется уравнению (1) [2]. Разложим функцию  в степенной ряд в окрестности частного решения :

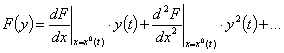                                                (3)

Производные функции  должны вычисляться в точках, соответствующих частному решению.

Перепишем уравнение (1) для возмущение с учетом (2):

 

                                               (4)

где

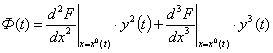                                              (4)

Слагаемые  включают все члены с (n≥2), то есть учитывают нелинейные добавки. Поэтому нелинейными членами в уравнении (4) в первом приближении можно пренебречь.

Таким образом, для эволюции малого возмущения мы получаем линейное уравнение

,    где                                                        (5)

Если уравнение (1) одномерно, то оно имеет стационарные решения, если двумерно, то стационарные и периодические [3]. С увеличением размерности исходной системы в общем случае усложняются типы возможных решений. С появлением современных компьютерных технологий нахождение этих решений не представляют каких-либо затруднений, благодаря чему можно проводить исследования, пользуясь аппаратом пространства состояния, не прибегая к аппарату передаточных функций.

Изменение параметра в уравнении может вызвать потерю устойчивости одного состояния (или режима функционирования) системы и переход ее в другое, отличное от первого состояния. Это явление называется бифуркацией (от слова «раздвоение»), а значение параметра, при котором оно происходит, точкой бифуркации. Насколько существенно изменяется состояние системы ниже и выше точки бифуркации определяет понятие грубости системы [4]. Суть данного понятия в том, что при малом изменении параметра грубая система хоть и изменяет в деталях режим функционирования, но не принципиально. С этой точки зрения для грубых систем переход через точку бифуркации означает смену одного структурно-устойчивого режима на другой. При этом в точке бифуркации система не является грубой: малое изменение параметра в ту или иную сторону приводит к резким изменениям состояния.

Предположим, что в результате бифуркации исходное стационарное состояния теряет устойчивость, и рождаются два новых устойчивых стационарных состояния. При этом вновь появившиеся два стационарных состояния расположены в непосредственной близости от исходного стационарного состояния, которое потеряло устойчивость (помечено звездочкой на рисунке 1в). Бифуркация такого типа называют мягкими, имея в виду, что вновь родившийся режим функционирования системы как бы появляются из режима, потерявшего устойчивость, и сосуществует рядом с ним.

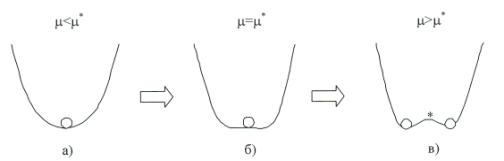
C:\Users\Aina\AppData\Local\Microsoft\Windows\INetCache\Content.Word\сканирование0009.jpg

Рисунок 1 -  «Мягкая» бифуркация

 

Другой пример бифуркации качественно представлен на рисунке 2. При  (рисунок 2а) шарик находится в устойчивом стационарном состоянии. При этом существует еще одно, неустойчивое состояние (помечено звездочкой на рисунке 2а). В точке бифуркации  устойчивое и неустойчивое состояния сливаются в одно (рисунок 2б). Далее они исчезают, и система выбирает новый режим (например, как это показано на рисунке 3в), который существенно отличается от предыдущего и не находится в непосредственной близости от исходного режима. Такой тип бифуркаций называют жестким.

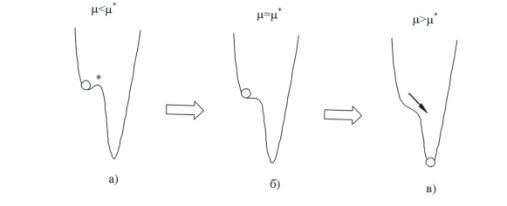
C:\Users\Aina\AppData\Local\Microsoft\Windows\INetCache\Content.Word\сканирование0010.jpg

Рисунок  2 - «Жесткая» бифуркация

 

Одним из новых шагов изучения бифуркаций явились результаты исследования теории катастроф, появившейся в 70-х годах, основанной на работах математика Рене Тома [5]. Именно жесткие бифуркации явились предметом анализа в теории катастроф.

 

Литература

1                        . Баландин Д.В., Коган М.М. О вычислении минимального уровня гашения внешних возмущений в задаче робастного - управления по выходу // Автоматика и телемеханика, 2003. -K211. - с. 128-137.

2                        . Баландин Д.В., Коган М.М. Синтез регуляторов на основе решения линейных матричных неравенств и алгоритма поиска взаимнообратных матриц // Автоматика и телемеханика, 2005. –J421. - с. 82-99.

3                        . Барабанов А.Е. Синтез минимаксных регуляторов – СПб: Изд-во СПбУ, 1996.

4                        . Colaneri P., Geromel J.C., Locatelli A. Control Theory and Design. An RH2 and RH∞ Viewpoint, Academic Press, 1997.

5                        . Бахилина И.М., Степанов С.А. Синтез грубых линейных квадратичных гауссовых регуляторов // Автоматика и телемеханика, 1998. -№27. - с. 96-106.