Технические науки/1. Механика

Zhiguts Yu.Yu., Kudlotiak C.H., Patai Z.C.

Uzhhorod National University, Ukraine

Transcarpathian Hungarian Institute, Ukraine

THE RESEARCH OF RESIDUAL STRESSES AT STEEL BY USING ZAKS METHODS

Introduction. When using thermal materials, a significant role is played by residual stresses, which is associated with a significant gradient of alloy synthesis temperatures, high cooling rates, an intense rate of passage of the combustion front in a metallothermic charge, and others. This, in turn, can cause residual stresses that have not been investigated in materials synthesized by termite methods.

Among the existing experimental methods for determining the residual stresses of the greatest distribution, the method of N.V. Kalakutsky for the details of the type of disk, the method of N.N. Davydenkov for the details of the ring type and the prismatic bar, the method of L.A. Glikman and D.I. Grigon for the bars of the two-tailed the cross section, the methods D.M. Shura, that is, the force method for determining the residual stresses, for which no measurements of deformation of parts are required on the basis of the approximate dependencies between stresses and deformations, but it can only be used for details of the correct geometric form of Hunnert’s methods that requires drilling conical holes, milling circular grooves and precision strain measurement that is extremely difficult measurement Zaks and method for parts such as solid and hollow cylinder [1].

Relevance of the problem. Due to the fact that the residual stresses for thermite alloys remain an almost unexplored region in the manufacture of cylindrical parts, there was a need for their evaluation and determination of the influence of these stresses on the strength of the synthesized alloy.

The theoretical part. The cylindrical part, in which the distribution of residual stresses is established, is subjected to successive straightening. In this case, the thickness of the treated layer is the same throughout the processing [1]. After removing each layer of thermite steel precisely measure the diameter and height of the cylindrical part. Tensions are determined by the formulas (1-3) [1]:

(1)

(2)

(3)

where σ_l, σ_t, σ_r – axial, tangential, radial residual stresses, MPa; E – modulus of elasticity, MPa; μ – Poisson coefficient; F – is the cross-sectional area corresponding to the internal diameter of the cylinder and which changes with a turning point, m²; F_z, F_в – area of the cross-section corresponding to the outer and inner diameter of the cylinder, mm; λ – relative change in cylinder height, mm/mm; v, v' – the relative change in the outer and inner diameters of the cylinder, mm/mm.

Output data in the calculation of the experimental method stress test in termite steel 40L (the boundary of the proportionality of the test material was 450 MPa, the conditional yield curve was 440 MPa, and the time resistance was 750 MPa): E=2,1×10⁵ MPa, μ=0,26, F=314,00 mm², F_z=310,87 mm, F_v=307,75 mm; λ=0,01 mm/mm; v=0,02 mm/mm, v'=0,01 mm/mm [2].

The scope of tests must ensure, within the required precision, an assessment of the mechanical properties achieved by: 1) a sufficiently small probability of α (errors of the first kind) – poor evaluation of the material with higher mechanical properties;
2) a sufficiently small probability of β-positive evaluation of materials with low properties (errors of the 2-nd kind). Taking into account a given degree of accuracy, the reliability of estimates of average characteristics in the case of small values of α and β, the number of samples is given by [3]:

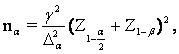(4)

where γ – coefficient of variation of the value of X; – limit relative error (tolerance in determining the average value ); – probability of error of the 1-st kind; – probability of error of the 2-nd kind; – the quintal’s of a normal distribution (a random variable corresponding to a given probability level).

The values of the error are chosen in the boundaries =0,01-0,05; values =0,05-0,1; =0,05-0,1; coefficient of variation γ=0,03. Accepted γ=0,03; =0,03; =0,05; =0,1. According to table 2.1 [3] ==1,96; ==1,28 and according to the formula (4) is determined by the required minimum number of samples to evaluate characteristics of thermite materials:

n_α=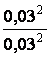∙(1,96+1,28)²=10,50.

We accept n_α=11 samples.

The evaluation of mechanical samples is performed after the determination of the average values of the properties of this material and the justification of the guaranteed minimum values of the characteristics of mechanical properties.

The selective mean value of the mechanical characteristic is determined by the formula from [3]:

(5)

where x_i – value of the mechanical characteristics of individual samples; n – number of samples tested.

The lower boundary of the mechanical characteristic is found from the equation:

(6)

where – the selective mean value of mechanical properties; S – selective mean square deviation; k – coefficient.

According to [3]:

(7)

where – the sample dispersion of the characteristics of mechanical properties.

Then

(8)

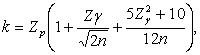(9)

where n – the total number of samples on the basis of which the values X and S are found; Z_p and Z_j – the normal distribution quantum for the probabilities p and j.

The probability of a guaranteed at 100=(1-) percent of cases of preservation conditions . For j=0,9, =1,28, α=0,1, p=1-α=0,9, =1,28:

.

At carrying out of experimental works the obtained results, by definition, axis =1,81 MPa, tangential =4,74 MPa and radial =7,45 MPa residual stress.

Conclusions. 1. Based on the analysis of the obtained results, it is proposed to consider the limiting condition criteria for the blanks of thermal steels the limiting strength of the part, the limiting residual deformations, excluding the further operation of the part, the loss of stability of the elements under the influence of power factors and the occurrence of cracks fatigue. 2. It is established by the Zaks method’s that during the formation of a steel termite steel ingot 45L the axial residual stresses are the smallest, tangential residual stresses 2,6 times larger than the axial, and radial in 4,1 times.

Literature:

1. Zaks M.N., Zakharov A.A., Belokurov V.N. Influence of conditions of fastening of a thin-walled rod of open profile on its density deformed state / Automotive industry. – 1979. – №3. – S. 26-28.

2. Zhiguts Yu.Yu. Alloys synthesized by metallothermic and SHS-processes (monograph). Uzhhorod: Grazhda, – 2008. – 276 p.

3. Koler Ya.D. Mathematical analysis of the accuracy of machining of parts. – K.: Technique. – 1976. – 200 p.