Технические науки/6. Электротехника и радиоэлектроника

Аслан-заде А.Г.

Россия

Неканонические режимы работы 12-пульсного ТСГ постоянного тока

Обретение функционально новой схемы трехфазного статического генератора (ТСГ) постоянного тока, обеспечивающего постоянный уровень амплитуд гармонического спектра относительно выпрямленного напряжения и потребляемого тока во всем диапазоне регулирования, выявило возможность существования неканонических режимов его работы при периодичности выпрямления m = 12 с 6-фазной неравнолучевой вторичной обмоткой трансформатора вместо 3-фазной «звезды» с нулевым выводом. Это выражается в том, что нарушается каноническое соотношение первичного фазного тока относительно повышающегося вторичного выпрямленного тока: уменьшается его действующее значение, в том числе сопровождающееся несимметрией пульсаций ступеней, уменьшением амплитуды 1-й гармоники и коэффициента мощности. При этом расчетная мощность трансформатора, несмотря на его усложнение, может понижаться. Эти режимы рассмотрены с учетом гармонического анализа, рекуперации энергии межфазным распределителем тока (МРТ) и расчетной константы многопульсного выпрямления.

Практическое значение закона первичных токов многофазных выпрямителей [1], для случая, когда сумма первичных фазных токов равна нулю, и впоследствии установленных закономерностей [2] для случаев, когда эта сумма не равна нулю, заключается в удобстве использования в расчетах новых схем априори известных величин. Однако существование более чем одного правила приводит к подтверждающемуся выводу [3] о возможности отступления от них, по крайней мере, в виде исключения.

Представленный в [4] трехфазный статический генератор (ТСГ) 12-пульсного выпрямленного напряжения, обеспечивающий без фильтра, на естественно управляемых 6-и вентилях и 2-х диодах постоянство уровня пульсаций во всем диапазоне регулирования, имеет ряд схемных модификаций разомкнутого типа. В наиболее простой из них вторичная обмотка трансформатора соединена в 3-фазную звезду с выведенным нулем [5], а в наиболее парадоксальной – в 6-фазную неравнолучевую звезду (рис.1) или более сложную схему [6]. Встречно включенные вторичные обмотки 6-фазной звезды или части каждой вторичной фазной обмотки более сложного варианта могут иметь два различных соотношения чисел витков , выбор которых взаимозависим от величин соотношений чисел витков обмоток уравнительных реакторов (Ур) , (0 < S > 1).

В первом случае S = 0, 732 и рассмотрено в [4] , а во втором S = 0, 3162 и показано в [6] и на рис.2, где стрелками обозначены направления токов через зачерненные вентили 5, 2, 8 и 9, 14, 16 за один такт выпрямления. Согласно решению косоугольных треугольников (рис.2), S = 0, 732 согласуется с данными: β₃ = 15⁰, β₁ = 45⁰, β₂ = 10, 89⁰, U_r1 = 1, 2247∙ U_ф , U_r2 = 1, 6772∙ U_ф, а S = 0, 3162 – с данными: β₃ = 17, 093⁰, β₁ = 18, 02⁰, β₂ = 15⁰, U_r1 = 1, 2721∙ U_ф , U_r2 = 1, 4448∙ U_ф. Здесь U_ф = 0a₁ = a₁b – фазное напряжение сети и вторичной обмотки W₁ приведенного трансформатора Тр₁, т.е. W₁ = W.

В первом случае 12-пульсное выпрямленное напряжение, формируемое на выходе вторичного моста несимметричное, а на выходе первичного моста – симметричное. Во втором случае картина взаимообратная. Это их отличает от простого случая (S=0,732, W₂= 0) с одной вторичной обмоткой трансформатора и симметричным 12-пульсным выпрямлением на выходе каждого моста [5]. Если S = 0, то и W₂ = 0. Поэтому зависимость между соотношениями обмоток

Ур и вторичными обмотками трансформатора Тр₁ отсутствует, а равенство w₂ = w₁ не позволяет получить угол между векторами смежных выпрямляемых напряжений, приемлемый для использования в составе 12N-пульсного ТСГ. Вместе с тем, если W₂ = 0, то S может принимать произвольное значение, но только при S = 0, 732 этот угол равен 30 эл.град., т.е. углу пульсации 12-пульсного ТСГ.

В простом случае (S = 0, 732, W₂ = 0), не имеющим рассогласований с законом первичных токов [1], единственным источником генерации ТСГ тока нулевой последовательности является регулирование магнитного потока трансформатора при неравенстве нулю суммы первичных фазных токов.

Из рассматриваемых случаев в первом (,) и втором (,) дополнительным источником генерации тока нулевой последовательности является обмотка W₂ трансформатора Тр₁.

В первом случае (рис.3) это приводит к увеличению U_d2 от 1, 7121∙U_ф до 2, 3389∙U_ф на выходе вторичного моста и несимметрии его формы относительно неизменного по величине и форме U_d1 = 1, 7121∙U_ф на выходе первичного моста (при равных нагрузках обоих мостов). Во втором случае (рис.4) – к увеличению U_d2 от 1,7121∙U_ф до 2,0198∙U_ф на выходе вторичного моста, но с принудительным нарушением симметрии при увеличении U_d1 от 1, 7121∙U_ф до 1, 7774∙U_ф на выходе первичного моста, связанном с симметрированием формы U_d2. В обоих случаях дополнительная генерация купируется обмоткой W₃ и в цепи, соединяющей эту обмотку с нулевым входным выводом, результат

трансформация тока нулевой последовательности от обмотки W₂ равен нулю. Именно поэтому расчетная мощность первичной обмотки W трансформатора Тр₁ не зависит от подключения обмотки W₂ вместо нулевого провода. Она зависит от угла несимметрии β = β₃ – β₂ на выходе первичного моста и величины его выпрямляемого напряжения U_r1 (рис.2).

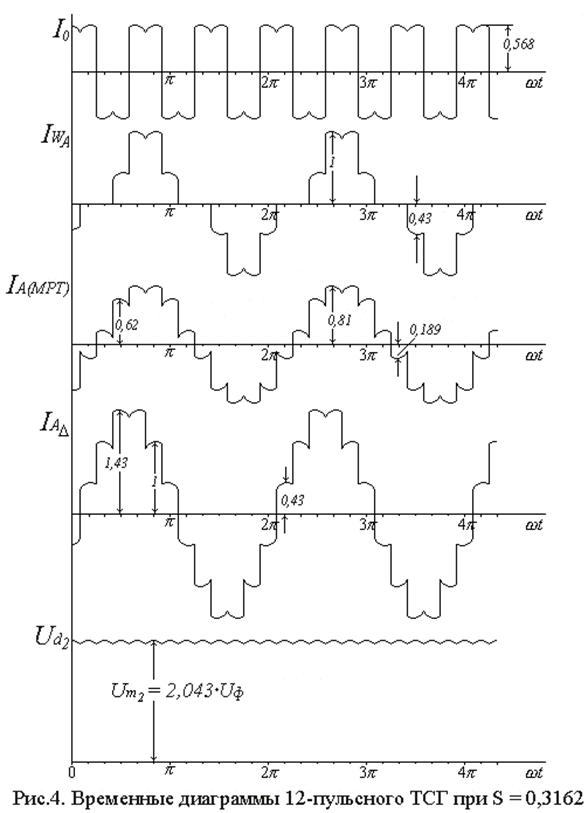
Среднее значение несимметричного 12-пульсного выпрямленного напряжения в первом случае (рис.3), при β = 4, 11 эл.град., на выходе

вторичного моста U_d2 = 1, 3945∙U_r2 = 2, 3389∙U_ф, а во втором случае (рис.4), при β = 2, 093 эл.град, на выходе первичного моста U_d1 = 1, 3972∙U_r1 =1, 7774∙U_ф, U_m1 = √2∙U_r1, U_m2 = √2∙U_r2. В простом случае, при β = 0 эл.град., U_d1 = U_d2 = 1,398∙U_r .

Так как формула (1) составлена относительно оси, показанной пунктирной линией на рис.3, то коэффициент B_n ряда Фурье равен нулю (четная функция) и для составления формулы коэффициента A_n ряда Фурье достаточно в каждое ее подынтегральное выражение ввести множитель , а в числитель – коэффициент 2. Тогда, коэффициент пульсаций К_п1,2 выпрямленного напряжения U_d1,2 во всем диапазоне регулирования:

Практическое значение имеет К_п2, т.е. уровень пульсаций на выходе вторичного моста, величина которого во втором случае равна канонической (1,398%) для m = 12, а в первом случае – 8,366%, т.е. больше, чем каноническая (5,714%) при m = 6 и естественном угле отпирания вентилей на 2, 652%.

В первом случае действующее значение тока I_I первичной обмотки W при симметрии 2-го вида, которой характеризуется ТСГ, определяется [2] по формуле:

где: 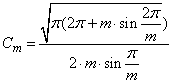, к_т = U_r1 /U_1, N = m/6 = 2, U_I – фазное напряжение обмотки W, C_N = C_m ≈ 1 – постоянная m-пульсного (m ≥ 4) выпрямления [4], I_d1 – среднее значение выпрямленного тока на выходе первичного моста. Однако коэффициент 0,502, численно соответствующий закономерности для первичного фазного тока при условии неравенства нулю суммы фазных токов, определен относительно меньшего симметричного тока I_d1 первичного, а не большего асимметричного тока I_d2 вторичного моста. Таким образом, фактически правильная величина не определяется общепринятым правилом.

Во втором случае амплитуда первичного фазного тока в 1, 2721/1, 2247 ≈ 1, 04 раз (отношение первичных выпрямляемых напряжений) больше, чем в первом случае, а угол несимметрии тока β = 2,093 эл.град. Независимо от величины угла β между выпрямляемыми напряжениями U_r1 и U_r2, ток I_I определяется частными коэффициентами трансформации амплитуд его ступеней (рис.2): и . В первом случае , во втором 0,4317. В соответствии со вторым случаем I_I = 0, 4943 к_т C_N I_d1, что не согласуется с формулой (3) и, тем самым, нарушает каноническое правило. Противоречие связано также и с отсутствием идентичности между формами 12-пульсных напряжений на выходе первичного и вторичного мостов. Для его решения следует принять в обоих случаях фактическое значение I_I определяемое относительно U_d1, а не U_d2 .

Действующее значение тока нулевой последовательности I₀, замыкающегося через обмотки W₃ и W₀, определяется частным коэффициентом трансформации , а через обмотки W₁ и W₂ – , где в первом случае , , а во втором случае , .

Действующее значение тока обмотки W₁ определяется, также независимо от величины угла β, частными коэффициентами трансформации амплитуд его ступеней (рис.2): и . В первом случае , а , во втором , а . Общий коэффициент трансформации в обоих случаях, с учетом функции обмотки W₃, равен к_т = W₁ /W. Искажение (рис.4) первичного тока в сторону 6-пульсного (несимметричного 12-пульсного), вследствие сдвига по фазе (β = 2, 093 эл.град.) между пульсациями тока, практически не сказывается на его действующем значении, т.к. 6 < m < 12, а при m ≥ 4 константа многопульсного выпрямления C_m ≈ 1.

Результаты вычислений показывают, что в первом случае коэффициент превышения К_т расчетной мощности трансформатора Тр₁ равен 0,5∙(1,0772 + 0,37 + 1,241) = 1,3441, где 1,241 и 1,0772 – К_т его обмоток соответственно W₁ и W, а 0,37 – К_т его обмотки W₃. Суммарное значение К_т равно 1,3441 + 0,2618 = 1,6059, где 0,2618 – К_т трансформатора Тр₂.

Во втором случае К_т трансформатора Тр₁ равен 0,5∙(1,0614 + 0,3197 + 1,0633) = 1,2222, где 1,0633и 1,0614 – К_т его обмоток соответственно W₁ и W, а 0,37 – К_т его обмотки W₃. Суммарное значение К_т равно 1,2222 + 0,2348 = 1,457, где 0,2348 – К_т трансформатора Тр₂.

Коэффициенты во втором случае, вопреки ожиданию, меньше, чем в простом случае (без обмотки W₂), т.е. когда К_т трансформатора Тр₁ равен 0,5∙(1,0772 + 0,37 + 1,0772) = 1,2622, где 1,0772 – К_т каждой из его обмоток W₁ и W, 0,37 – К_т его обмотки W₃, а суммарное значение К_т равно 1,2622 + 0,2618 = 1,524, где 0,2618 – К_т трансформатора Тр₂. Объясняется это тем, что U_r2 > U_r1 (наличием обмотки W₂) и увеличением U_r1, а также отступлением (рис.4) от закона первичных токов (изменением соотношения амплитуд ступеней первичного фазного тока). Парадокс в том, что уменьшение коэффициента К_т достигается не за счет лучшего использования обмоток трансформатора по напряжению и току, а за счет купирующего действия обмотки W₃, несмотря на включение дополнительной обмотки W₂ с плохим использованием. Ничтожно малая разность (0,067) между К_т простого (1,524) и К_т второго (1,457) случая с 12-ю неравномерно нагруженными выпрямляющими диодами и существенно более мягкой внешней характеристикой, относительный коэффициент которой A = 12/2πab в первом, втором и простом случае равен соответственно 1,3282; 1,5036 и 0,91, – свидетельство в пользу простого случая. Здесь a = U_d2/U_ф соответственно равно 2,3389; 2,0198; 1,712, b = I_d /I_w соответственно равно 0,6148; 0,62886; 0,6148.

При отсутствии МРТ (трансформатор Тр₂), сеть должна содержать нулевой вывод от нейтрали вторичной обмотки трансформатора, первичная обмотка которого соединена в треугольник. Только тогда в линейном токе, например, фазы A сети (рис. 3 и 4), определяемом разностью фазных токов и ТСГ, не будет гармоник тока I₀.

Подключение МРТ (мощность Тр₂ ≈ 20% от мощности Тр₁) купирует воздействие на сеть тока I₀, обеспечивая рекуперацию энергии за счет уменьшения в √3 раз амплитуды линейного тока , совпадающего по фазе с током . В обоих случаях . Данный способ рекуперации заключается в циркуляции части энергии между МРТ и ТСГ, уменьшающей, тем самым, отбираемую из сети мощность на 42,3%. Высокие энергетические показатели ТСГ с МРТ – существенный противовес, по крайней мере в простом случае, повышению K_T за счет Тр₂.

Общепринятый метод расчета действующего значения 1-й гармоники I_1A первичного тока [7] идеализирован методологически, так как при этом сопоставляется прямоугольно-ступенчатая форма первичного тока с вспомогательной синусоидой, проводимой через средние точки ее ступеней. Фактически осуществляется ступенчатое интегрирование вспомогательной синусоиды (с учетом амплитуд ступеней тока) относительно оси разложения в ряд Фурье, проходящей через точку ее пересечения с осью абсцисс. Тогда, например, для первичного тока коэффициент A_n (результат вывода формулы для A_n приведен для первой гармоники) четной функции ряда Фурье при β = 0 эл.град., в первом (рис.3) и простом случае, можно представить, с учетом использования вспомогательной синусоиды, в виде двух сумм интегралов:

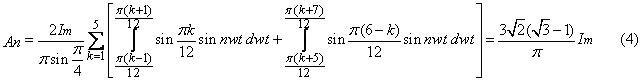
где: I_m – амплитуда фазного тока обмотки W_A трансформатора Тр₁, k = 2i – 1, i = 1, 2, 3. Результаты вычислений по общепринятому методу имеют при m = 12 завышенные значения. Объясняется это неравенством действующих значений сопоставляемых токов при их равной длительности. Неточность метода проявляется при симметричной 6-ступенчатой полуволне тока ТСГ (при m = 12, вместо 0,9775), а в случае ее меньшей длительности λ, например, λ = 120 эл.град. полуволны тока I_WA без МРТ (рис.3 и 4) он вообще неприемлем. Это следует из того, что результат деления λ полуволны вспомогательной синусоиды на m/2 интервалов дискретности превышает число ступеней тока. Форма тока I_WA с отношением амплитуды промежуточной ступени к крайней √3 + 1 () при S = 0, 732 свидетельствует о наличии в его составе 3-й гармоники и поэтому разложение в ряд Фурье, в этом случае, имеет только методологическое значение. Но в первичном токе ряда выпрямителей с МРТ, например, по схеме вторичной стороны (S = 0,732 на рис.1) нет 3-й гармоники, а λ = 150 эл.град. Отсюда и необходимость в математически точном разложении первичного тока в ряд Фурье.

Однако разложение первичного тока в ряд Фурье без вспомогательной синусоиды, на этапе приведения к общему знаменателю вида n² – 1, приводит при n = 1 к неопределенности или к запрету на деление . Обход этого препятствия возможен применением свойства [8] определенного интеграла на этапе разложения, предваряющего приведение к общему знаменателю n² –1. Тогда, для первичного тока с осью разложения от средней точки его полуволны, коэффициент A_n (результат вывода формулы для A_n приведен для первой гармоники) четной функции ряда Фурье можно представить без использования вспомогательной синусоиды в виде одной суммы интегралов:

Аналогично для первичного тока I_A(МРТ), также без использования вспомогательной синусоиды, можно представить A_n в виде одной суммы интегралов:

При β = 2,093 эл.град. числители формул (5) и (6) практически равны, и поэтому отношение коэффициентов A_n можно принять равным √3. Коэффициент искажения ν (отношение действующего значения первой гармоники первичного тока I_1A к его полному значению I_A∆), равный коэффициенту мощности χ [9] при коэффициенте сдвига cosφ = 1, в первом случае ν = I_1A /I_A∆ = 0,79814/0, 8165 = 0,9775, а во втором случае ν = I_1A /I_A∆ = 0,797/0,8165 = 0,9761. Уменьшение I_1A при постоянстве I_A∆ свидетельствует о генерации 5-й и 7-й гармоник, компенсирующих уменьшение его первой гармоники в действующем значении искажаемого тока. Справедливость ν = 0,9775 и для тока I_A(МРТ) в первом случае связана с идентичностью формы и соотношения амплитуд ступеней токов I_A∆ и I_A(МРТ): ν = I_1A /I_{A (МРТ)} = 0, 4608/0, 4714 = 0, 9775. Отличие только в масштабах. Во втором случае ν для тока I_A(МРТ) меньше, чем для тока I_A∆, т.е.: ν = I_1A/I_A(МРТ) = 0, 4602/0, 4714 = 0, 9762. Как видно, при искажении (рис.4) первичного тока в сторону 6-пульсного (несимметричного 12-пульсного), происходящем вследствие сдвига по фазе (30 ± 2·β) эл.град. между пульсациями ступеней тока, уменьшается действующее значение первой гармоники линейного тока I_1A, замыкающегося через МРТ, но при постоянстве его полного действующего значения I_A(МРТ). Это также свидетельствует о генерации 5-й и 7-й гармоник в искажаемом токе. Данное сопоставление справедливо при приведении к одной и той же величине первичного фазного напряжения с использованием коэффициентов трансформации 1,2247 и 1,2721 между напряжениями U_r1 и U_ф, т.е. в формулах (4), (5), (6) для вычисления действующего значения первой гармоники необходимо разделить A_n на 1,2247∙√2 или 1,2721∙√2. Рассмотренное искажение не соответствует теоретически канонической форме первичного тока при симметричном 12-пульсном выпрямлении на вторичной стороне ТСГ.

Неканонические режимы работы 12-пульсных ТСГ с 6-фазной неравнолучевой вторичной обмоткой трансформатора вместо 3-фазной «звезды» с нулевым выводом [10] – одно из двух свидетельств нарушения [3] и закона [1] и закономерностей [2] первичных токов многофазных выпрямителей.

Выводы:

1. Рассмотренные режимы работы 12-пульсных ТСГ постоянного тока свидетельствуют о частной возможности отступления от всех канонических закономерностей первичного тока многопульсных выпрямителей.

2. Двойное предназначение МРТ вносит его в число не только необходимых, но и энергетически высокоэффективных элементов преобразователей с неуравновешенной магнитной системой трансформатора.

3. Рассмотренное математически точное разложение первичного тока в ряд Фурье, в отличие от общепринятого метода с использованием вспомогательной синусоиды, применимо при любой его длительности и с точностью, не зависящей от числа ступеней.

Литература

1. Чернышев М.А. Закон первичных токов многофазных мутаторов. «Электричество». 1940. № 6.

2. Абдулаев А.А., Аслан-заде А.Г. Анализ многопульсного выпрямления. «Электричество». 1977. № 8.

3. Аслан-заде А.Г. О возможности нарушения закона первичных токов многофазных выпрямителей. http://goo.gl/ThzucD Materials of the XII international scientific and practical conference. “Modern scientific potential- 2016”. Volume 19 Technical sciences Physics. Sheffield science and education ltd 2016. C 42 – 44. (www.rusnauka.com Конференции 2016 года. Современный научный потенциал-2016. Технические науки).

4. Аслан-заде А.Г. Улучшение гармонического состава токов и напряжений тиристорного выпрямителя посредством использования токов нулевой последовательности при управлении. «Электричество». – 2013. – №11.

5. Аслан-заде А.Г. Патент № 2340073 (RU) БИ, 2008, №33 и БИ, 2009, №10.

6. Аслан-заде А.Г. Патент № 2469457 (RU) БИ, № 34, 2012.

7. Шляпошников Б.М. Игнитронные выпрямители для тяговых подстанций железных дорог. М.: Трансжелдориздат. – 1947. – 736 с.

8. Рывкин А.А. , Рывкин А.З., Хренов Л.С. Справочник по математике. М.: Высш.шк.,1987. – 480 с.

9. Каганов И.П. Электронные и ионные преобразователи. Ч. 3. М. – Л. 1956.

10. Аслан-заде А.Г. Основные этапы построения трехфазного статического генератора постоянного тока. https://goo.gl/5Fmi1G News of Science and Education. № 8, 2017. Volume 2. Sheffield science and education ltd 2017. C 8 – 21. (www.rusnauka.com Конференции 2017 года. Перспективы мировой науки – 2017. Технические науки).