Економічні науки / 1. Банки і банківська система
 
К.е.н., доц. докторант Кузьмак О.М.
Тернопільський національний економічний університет

Ризик-менеджмент у забезпеченні фінансової

стійкості банків

Для ефективного управління фінансовою стійкістю банківських установ значну роль відіграє система ризик-менеджменту, що базується на передових технологіях та світовому досвіді управління ризиками. В умовах глобалізації та інтеграції банківського бізнесу, посилення конкурентної боротьби та зростання ризиків банківської діяльності постають завдання забезпечення фінансової стійкості, оптимізації співвідношення конкуруючих характеристик - ризику та дохідності. Саме тому необхідним є удосконалення підходу прийняття рішень щодо забезпечення фінансової стійкості банку на основі довільного критерію, що передбачає визначення ймовірностей настання певних станів банку в контексті стабільності його роботи.

Так у світовій практиці розрізняють три основні види фінансової стійкості банку за стабільністю його роботи:

а) нормальна стійкість, яка характеризується стабільною діяльністю, відсутністю неплатежів чи затримки виконання своїх зобов’язань, стабільною рентабельністю;

б) нестійкий фінансовий стан, що характеризується затримкою платежів, неможливістю своєчасно виконувати окремі свої зобов’язання, низьким рівнем рентабельності тощо;

в) кризовий фінансовий стан, який характеризується регулярними неплатежами, наявністю простроченої заборгованості тощо.

Кризовий фінансовий стан може призвести до неспроможності банку фінансувати поточну діяльність, здійснювати платежі та виконувати свої зобов’язання, а в кінцевому рахунку – до банкрутства.

Отже розглядаємо ситуацію трьох ймовірних станів банку коли треба прийняти управлінське рішення з m існуючих альтернатив (x₁, ..., x_m) за певним критерієм, що є загальноприйнятим у ризик-менеджменті [3] (максимуму математичного сподівання прибутків, мінімуму ризику, максимізація доходності, тощо).

Банк може опинитися у одному з станів (стійкий, нестійкий, кризовий), описаних вище. Позначимо ці стани відповідно q₁- стійкий, q₂ - нестійкий, q₃ - кризовий. Вважаємо, що відомі фінансові результати банку у цих станах:

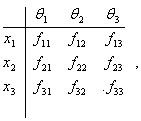
Але ймовірності настання цих станів р(q₁)=р₁, р(q₂)=р₂, р(q₃)=р₃ не можуть бути визначені банком.

Відповідно до підходу Гіббса-Джейнса, такі ймовірності потребують максимізації функції . При відсутності обмежень на ймовірності -р₁=р₂=р₃=1/3, але якщо є інформація по хоча б одній ймовірності їх значення можуть бути ідентифіковані.

Нехай банк знає ймовірність настання певного одного стану q₁, q₂, q_3, наприклад - відома ймовірність р(q₁)=р₁.

Отже максимізуємо - і врахуємо, що р₃=1 – р₁- р₂, тоді:

Частинна похідна становить: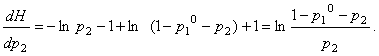

Прирівнюючи її до нуля, отримаємо:

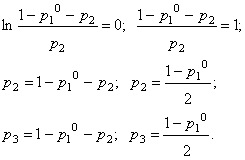
Отже, якщо відомо ймовірність одного з станів р₁, то ймовірності інших станів за підходом Гіббса-Джейнса рівні:

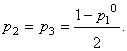
Нехай р(q₂)=kр(q₁), р₂=kр₁, тобто ймовірність стану q₂ в k разів більша, отже функція Н має вид:

Часткова похідна по р₁становить:

При прирівнюванні похідної до нуля, знаходимо р_1, що надає Н максимального значення:

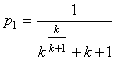. ( 1.1)

Ймовірність

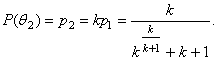( 1.2)

І ймовірність третього стану банку:

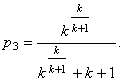( 1.3)

У таблиці 1.1 наведено приклад вибору оптимального рішення згідно з формулами (1-3) при k=2. Як видно з наведених обчислень тут кращим рішенням є , оскільки його математичне сподівання .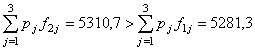

Таблиця 1.1

Вибір рішення щодо забезпечення фінансової стійкості банку за підходом Гіббса-Джейнса

Джейнс	Ймовірності				Математичне сподівання
Коефіцієнт	p1	p2		p3
k=2	0.2179883	0.4359767		0.3460349
Рішення	Кількісні оцінки (умовні одиниці)
x1	2100	9000	2600		5281.256742
x2	2400	8600	3000		5310.676542
Бернуллі	Ймовірності				Математичне сподівання
Коефіцієнт	p1	p2	p3
k=2	0.2	0.4	0.3
Рішення	Кількісні оцінки (умовні одиниці)
x1	2100	9000	2600		4800
x2	2400	8600	3000		4820

За принципом Бернуллі ймовірності треба вважати рівними

, а і, з рівності, отримаємо:

Тому математичне сподівання для першого рішення більше, ніж математичне сподівання для рішення .

Отже, складовими забезпечення фінансової стійкості є прибутковість та ефективна система управління ризиками.

Література

1. Алавердов А.Р. Стратегический менеджмент в банке / А.Р. Алавердов. – М.: Московская финансово–промышленная академия. – 2005. – 157 с.;

2. Валравен К.Д. Управление рисками коммерческого банка / К.Д. Валравен. – Вашингтон: Институт экономического развития Мирового банка, 1993. – 94 с.;

3. Івченко І.Ю. Моделювання економічних ризиків і ризикових ситуацій. Навчальний посібник. / І.Ю. Івченко. – К.:ЦУЛ, 2007. – 344 с.