Курінь К.О., Фролов О.В., Весельська О.М.

Національний авіаційний університет

Методи інваріантно-просторового кодування в технологіях стиснення зображень

Актуальність. Життєдіяльність сучасного суспільства неможливо уявити без інтегрованих розгалужених інформаційно-телекомунікаційних систем (ІТКС), що забезпечують своєчасну та надійну доставку даних між абонентами.

Найважливішим показником ефективності функціонування ІТКС є час доставки інформації . Зменшення часу доставки даних – одна з найбільш актуальних задач сучасної теорії інформації. Найбільш суттєвий вплив на збільшення часу доставки даних чинить із одного боку обмеженість характеристик технічного забезпечення ІТКС, а з іншого боку – великі обсяги даних, що оброблюються та передаються. Модернізація телекомунікаційних технологій є досить дорогим і тому не завжди доцільним способом вирішення даної проблеми. Тому поряд з розвитком технічної бази необхідно здійснювати модернізацію інформаційного забезпечення ІТКС. Для скорочення обсягів даних, що обробляються та передаються в інформаційній системі слід інтегрувати в неї системи стиснення даних. Як відомо, найбільша частка інформації міститься відео- та графічних даних. Частка інформаційного потоку на базі графіки займає до 90% від загального потоку інформації, що обробляється в ІТКС. Таким чином одним з найважливіших завдань|задач| сучасної теорії інформації є|з'являється| розробка і реалізація нових методів стиснення, що забезпечують максимальний ступінь|міру| компресії з|із| одночасною мінімізацією рівня спотворень даних у відновленій інформаційній структурі.

Мета дослідження. Метою дослідження є розробка аналітичної моделі методу кодування двійкових послідовностей у складі квантованих трансформант зображення, який би забезпечував вищі ступені стиснення в порівнянні з існуючими методами без внесення спотворень даних у відновлену інформаційну структуру.

Викладення основного матеріалу. В ході попередніх досліджень був розроблений метод кодування даних, заснований на усуненні просторово-кореляційної надмірності шляхом виявлення кореляційних закономірностей в двійкових послідовностях (ДП) за ознакою – сумарною бітовою кореляцією [6] – метод інваріантно-просторового кодування (ІПК).

Було запропоновано інтегрувати метод ІПК в технологію стиснення зображень в якості методу кодування квантова нихтрансформант. Завданням|задачею| етапу кодування квантованих трансоформант є|з'являється| формування коду ІПК для кожної з бітових площин сегментів зображення на базі виявлення кореляційної надмірності з урахуванням сумарної бітової кореляції бітових шарів сегментів зображення.

В результаті|унаслідок| здійснення даного кроку кодером формуються масив значень кодів ІПК для|стискати| зображення, а також масив значень кореляційної ознаки – сумарної бітової кореляції, які необхідні декодеру для подальшого однозначного декодування даних.

Процедура кодування відбувається у наступні етапи:

1. Зиґзаґ-сканування. Використання цього принципу зчитування двійкових даних доцільне, оскільки воно забезпечить зменшення значення сумарної бітової кореляції.

2. Формування масиву із значеннями кореляційної ознаки – сумарної бітової кореляції. Дана ознака розраховується для кожного з восьми бітових шарів кожного сегменту зображення.

3. Розрахунок значень кодів ІПК для двійкових послідовностей у складі бітових шарів зображення. – масив значень кодів ІПК. Структурно-аналітична модель кодування двійкових послідовностей у складі квантованих трансформант на базі ІПК зображена на рис. 1.

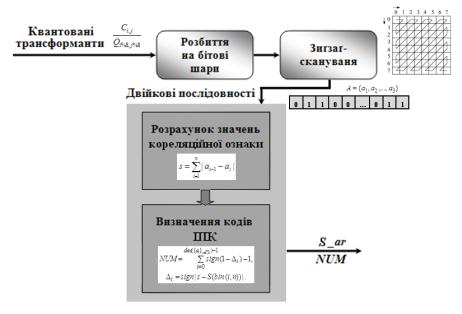
Рис. 1. Структурно-аналітична модель кодування ДП методом ІПК у складі квантованих трансформант зображення

Було проведено також оцінку коефіцієнтів стиснення згідно методів ІПК для ряду тестових двійкових послідовностей у складі трансформант дискретного косинусного перетворення (ДКП), та інших методів кодування:

–методів нестатистичного кодування – ДСК, НРПК (в режимі без втрат) [4,5] – для ряду тестових двійкових послідовностей у складі трансформант ДКП;

–методів статистичного кодування – арифметичного кодування, методу Хаффмена, LZW, RLE [8] – для трансформант, у складі яких перебувають тестові двійкові послідовності.

Отримані результати дозволили зробити наступні висновки – розроблений метод ІПК забезпечує виграш за значенням коефіцієнта стиснення при кодуванні трансформант (ДКП) в середньому:

- в 1,11 разів с порівнянні з методом ДСК;

- в 1,15 разів с порівнянні з методом НРПК;

- в 1,68 разів с порівнянні з методом Хаффмена;

- в 1,27 разів с порівнянні з методом арифметичного кодування;

- в 2,34 разів с порівнянні з методом RLE;

- в 1,36 разів с порівнянні з методом LZW.

Висновки. В ході дослідження отримані такі науково практичні результати:

1. Визначено роль і місце алгоритмів стиснення зображень для скорочення часу доставки даних в ІТКС. Обґрунтовано доцільність підвищення ступеня стиснення і, як наслідок, подальшої розробки нової технології стиснення зображень.

2. Наукова новизна досліджень, описаних у даному розділі, полягає в наступному: вперше розроблено структурно-аналітичну модель кодування-декодування двійкових послідовностей у складі квантованих трансформант зображення та їх відновлення, що на відміну від існуючих підходів:

- враховує доцільність розбиття вмісту квантованих трансформант на бітові площини замість представлення безпосередніми десятковими значеннями компонент, що дозволяє врахувати кореляційні закономірності;

-враховує можливість представлення бітових площин трансформанти кодами ІПК.

Література:

1. Урсул А.Д. Нестатистические подходы в теории информации / А.Д. Урсул // Вопросы кибернетики.–1967.–№2.– С. 88–93.

2. Юдін О.К. Кодування в інформаційно-комунікаційних мережах: – Монографія. - К.: НАУ, 2007.-308с.

3. Юдін О.К. Обгрунтування ефективності двоознакового структурного кодування у двійковому поліадичному просторі / О.К. Юдін // Проблеми інформатизації та управління: Збірник наукових праць. – К.:НАУ, 2006. – Вип. 2(17). – С.137–141.

4. Юдін О.К. Метод кодування двійкових послідовностей за кількістю бітових переходів / К.О. Курінь, М.Г. Луцький, О.К. Юдін // Наукоємні технології. – К.: Вид-во Нац. авіац. ун-ту «НАУ-друк», 2012. – № 4 (16). – С. 98-102.

5. Д. Селомон. Стиснення|стиснення| даних, зображень і звуку. – М|м-код|.:Техносфера, 2006. – 386с.