Математика/1.Дифференциальные и интегральные уравнения

К. ф.-м. н. Симотюк М. М., аспірант Хомяк Д. В.

ІППММ ім. Я.С. Підстригача НАН України, Львів

Задача з інтегральними умовами для

навантаженого гіперболічного рівняння

Задачі з інтегральними умовами виникають при математичному моделюванні процесів поширення тепла, процесів вологопреносу у капілярно-пористих середовищах, демографічних процесів, динаміки популяцій у випадках, коли межа області протікання процесу є недоступною для безпосередніх вимірювань або коли певні фізичні величини неможливо обчислити безпосередньо, але є відомими їхні усереднені значення. Для рівнянь із частинними похідними задачі з інтегральними за виділеною змінною та умовами періодичності за рештою змінних вивчалися у роботах М.Т.Дженалієва, М.І.Іванчова, В.С.Ільківа, Н.І.Іонкіна, П.І.Каленюка, А.М.Кузя, М.І.Матійчука, О.М.Медвідь, А.М.Нахушева, З.М.Нитребича, Б.Й.Пташника, Л.С.Пулькіної, М.М.Симотюка, І.В.Тіхонова, Л.В.Фардіголи, П.І.Штабалюка, М.Й.Юрчука (див. праці [1–6] та бібліографію в них).

В останні десятиріччя зріс інтерес до вивчення крайових задач для рівнянь із частинними похідними, навантажених значеннями невідомої функції та її похідних на скінченній кількості гіперплощин [1, 4]. Це зумовлено тим, що такі задачі виникають при моделюванні процесів фільтрації, керування і регулювання рівня грунтових вод [5], а також при дослідженні деяких обернених задач, наближеному розв’язуванні крайових задач для інтегро-диференціальних рівнянь.

У даній роботі розглядаємо задачу з інтегральними умовами (ваги в яких є показниковими функціями) для навантаженого строго гіперболічного рівняння.

Будемо використовувати такі позначення: – -вимірний тор , , , , , , , – символ Кронекера,

, , – простір, який є поповненням множини тригонометричних поліномів скінченного порядку за нормою

,

– банахів простір функцій таких, що для кожного фіксованого похідні , , належать до простору і як елементи цього простору є неперервними за на ; норму в просторі визначаємо формулою

,

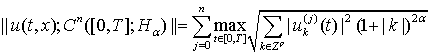Розглянемо задачу

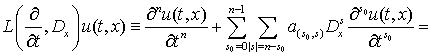
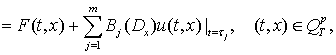(1)

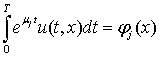, , , (2)

де , , , , , , , , , – строго гіперболічний вираз,

Нехай , , – корені многочлена (зі строгої гіперболічності виразу випливає, що для кожного усі числа , є дійсними та різними). Для формулювання умов розв’язності задачі (1), (2) запровадимо такі позначення:

, , ,

, ,

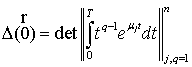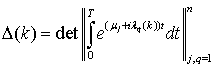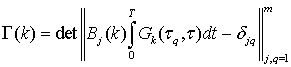де , , – функція Гріна такої інтегральної задачі для звичайного диференціального рівняння:

,

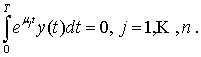
Якщо , то функція Гріна існує і визначається однозначно.

Теорема 1. Нехай для всіх векторів виконуються нерівності , . Нехай існують сталі такі, що для всіх (крім скінченної кількості) векторів виконуються нерівності

(3)

(4)

Якщо , , , то у просторі існує єдиний розв’язок задачі (1), (2), який неперервно залежить від функцій та , .

Для з’ясування питання про можливість виконання оцінок (3), (4) застосовано метричний підхід, на підставі якого отримано такі результати.

Теорема 2. Для майже всіх (стосовно міри Лебега в ) чисел нерівність (3) виконується для всіх (крім скінченної кількості) векторів , якщо .

Теорема 3. Нехай існує така стала , що для всіх (крім скінченної кількості) векторів виконується нерівність

.

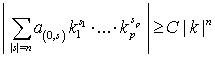Тоді для майже всіх (стосовно міри Лебега в ) векторів нерівність (4) виконується для всіх (крім скінченної кількості) векторів , якщо .

Результати роботи переносяться на випадок задач з інтегральними умовами для систем навантажених гіперболічних рівнянь.

Література

1. Дженалиев М.Т. К теории линейных краевых задач для нагруженных дифференциальных уравнений. Алматы: Компьютерный центр ИТПМ, 1995. – 270 с.

2. Ільків В.С. Задача з інтегральними умовами для системи диференціальних рівнянь з частинними похідними і змінними коефіцієнтами // Вісник ДУ “Львівська політехніка”. Прикл. матем. – 1999. – № 364. – С. 318–323.

3. Кузь А.М., Пташник Б.Й. Задача з інтегральними умовами за часом для рівнянь, гіперболічних за Гордінгом // Укр. мат. журн. – 2013. – 65, № 2. – С. 252–265.

4. Медвідь О.М. Інтегральна задача для навантажених рівнянь із частинними похідними // Математичний вісник НТШ. – 2007. – Т. 4. – С. 201–213.

5. Нахушев А.М. Краевые задачи для нагруженных интегро-дифференциальных уравнений гиперболического типа и некоторые их приложения к прогнозу почвенной влаги // Дифференц. уравнения. – 1979. – 15, №1. – С. 96–105.

6. Пташник Б.Й., Ільків В.С., Кміть І.Я., Поліщук В.М. Нелокальні крайові задачі для рівнянь із частинними похідними – К.: Наук. думка, 2002. – 416 с.